
Эпюры ВСФ
.pdf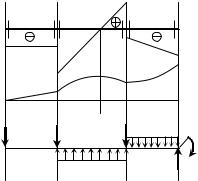
|
|
Участок 5–6: изменение момента 9 ql2 - |
ql2 =8 ql2 ; площадь эпюры Qy |
||||||||||||||
2l 4ql =8 ql2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
На всех участках противоречий нет. |
|
|
|
|
|
|
|||||||||
|
|
Имея определенный навык, все эти проверки можно сделать устно и |
|||||||||||||||
достаточно быстро. Аналогично можно проверить ответы во всех других рас- |
|||||||||||||||||
смотренных примерах. Следует отметить, что допущенная на эпюрах ошибка |
|||||||||||||||||
проявляется обязательно в нескольких противоречиях при проверках. |
|
||||||||||||||||
|
|
Чтобы овладеть навыками быстрой и уверенной проверки эпюр, надо |
|||||||||||||||
научиться решать так называемые «обратные задачи». Рассмотрим на приме- |
|||||||||||||||||
ре эпюр в балках. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Пример 9. |
Задана эпюра поперечных сил (рис. 48а). Требуется, со- |
||||||||||||||
блюдая приближенно масштаб, показать вид нагрузки и вид эпюры изги- |
|||||||||||||||||
бающих моментов. |
|
|
|
|
|
а) |
|
|
|
|
|||||||
|
|
Решение. |
|
|
|
|
|
|
|
5 |
6 |
|
|||||
|
|
|
|
|
|
|
|
1 |
2 3 |
ЭпQy |
|||||||
|
|
Вид нагрузки и эпюры M X |
надо оп- |
|
4 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||
ределить, используя лишь эпюру Qy , и |
|
|
|
|
|
||||||||||||
только потом сопоставить их между собой. |
б) |
|
|
|
ЭпMx |
||||||||||||
Начнем с эпюры M X (рис. 48б). На участке |
|
|
|
|
|
||||||||||||
1–2 |
функция эпюры MX (z) линейная, так |
в) |
|
|
|
|
|||||||||||
как |
M |
′ (z) = Q |
(z) = const . Начальный мо- |
|
|
|
|
|
|||||||||
|
|
|
X |
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
мент эпюра Qy |
не определяет, поэтому мо- |
Рис. 48. Обратная задача |
|
||||||||||||||
жем принять M X ,1−1 = 0 (рис. 48б). Из этой |
|
||||||||||||||||
|
|
|
|
|
|||||||||||||
нулевой точки проводим наклонную прямую вверх с учетом направления |
|||||||||||||||||
осей |
z и |
M |
X |
, а также M |
X |
′ (z) = Q (z) < 0 . Первая ненулевая ордината опре- |
|||||||||||
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
||
деляет масштаб эпюры M X , так как она численно равна площади прямо- |
|||||||||||||||||
угольника на эпюре Qy . |
|
MX (z) |
|
|
|
|
|
|
|
||||||||
|
′ |
На |
|
участке |
3–4 |
|
– |
квадратная |
парабола, |
|
так |
как |
|||||
M |
(z) = Q (z) |
− линейная. Выпуклость кривой направлена вверх, так как |
|||||||||||||||
|
X |
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
на стыке сечений 2–2 и 3–3 (рис. 46б) должен быть перелом с увеличением |
|||||||||||||||||
производной без изменения знака. Проводим параболу с экстремумом под |
|||||||||||||||||
нулевой точкой на эпюре Qy . При этом ординаты показываем, оценивая при- |
|||||||||||||||||
близительно площади треугольников на эпюре Qy . |
|
|
|
|
|||||||||||||
|
′ |
На |
участке |
5–6 |
|
MX (z) |
тоже |
квадратная |
парабола, |
так |
как |
||||||
M |
(z) = Q (z) |
− линейная. На стыке сечений 4–4 и 5–5 (рис. 46б) должен |
|||||||||||||||
|
X |
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
быть перелом со сменой знака производной. Так как по модулю производная |
|||||||||||||||||
должна возрастать, то выпуклость кривой получается направленной вниз. |
|||||||||||||||||
Ординату M X ,6− 6 показываем с учетом площади трапеции на эпюре Qy . |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
39 |
|
|
|
|
|
|

Покажем вид нагрузки на балку. По эпюре поперечных сил невозможно различить сосредоточенные нагрузки и опорные реакции, да в этом и нет необходимости. В местах скачков на эпюре Qy показываем сосредоточенные
силы.
На левом конце балки сила направлена вниз, так как Qy отрицательна
и, следовательно, сила должна вращать балку против часовой стрелки. При переходе от сечения 2–2 к сечению 3–3 Qy увеличивается с тем же знаком.
Поэтому добавляется сосредоточенная сила, направленная в ту же сторону. По величине вектор силы желательно показывать пропорционально величине скачка на эпюре Qy .
Следующую сосредоточенную силу надо приложить между сечениями 4–4 и 5–5. Поскольку скачок на эпюре Qy , как и в двух предыдущих случаях,
вниз, то сила опять направлена вниз.
На правом конце балки скачок на эпюре Qy вверх, поэтому сосредото-
ченная сила направлена вверх. Направление этой силы можно обосновать и отрицательным знаком Qy (сила должна вращать отсеченную часть против
часовой стрелки).
На участках 3–4 и 5–6 функция Qy (z) линейная и потому надо показать
равномерно распределенную нагрузку. На участке 3–4 интенсивность распределенной нагрузки qY больше, чем на участке 5–6, так как наклон линии
(а значит и производная от Qy по модулю) больше. Направление распреде-
ленной нагрузки на участке 3–4 можно установить, исходя из того, что она уменьшает по модулю Qy от сил, направленных вниз, и значит направлена
им навстречу. Другой вариант – определить знак qY по дифференциальной
зависимости
dQdzy = −qy (z) .
На участке 3–4 производная от Qy положительна (функция возрастает), поэтому qY отрицательна, т.е. направлена вверх (рис. 48в).
На участке 5–6 наклон касательной на эпюре Qy меняет знак (рис. 48а),
следовательно, меняется направление распределенной нагрузки (рис. 48в). Теперь, сопоставляя эпюру M X и нагрузку, видим, что выпуклость
кривых на эпюре соответствует «правилу паруса». Так как на правом конце балки получился изгибающий момент с растянутыми волокнами сверху, в нагрузке надо добавить на правом конце сосредоточенный момент, направленный по часовой стрелке.
Задача решена. Если на эпюре Qy будет задана квадратная парабола, то на соответствующем участке интенсивность распределенной нагрузки будет
40
меняться по линейному закону, а на эпюре M X покажем кубическую параболу.
7. ЭПЮРЫ ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ В СОСТАВНЫХ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛКАХ
Объектом сопротивления материалов является брус. Системы, составленные из брусьев, рассматриваются в строительной механике. Но в данном учебном пособии уделим внимание и несложным стержневым системам. Начнем с многопролетных (т.е. составных) статически определимых балок. Система называется статически определимой, если все усилия в ней можно найти из уравнений равновесия.
При расчете составных балок выполняются следующие операции.
1.Выделяем основные и второстепенные элементы и отражаем это на поэтажной схеме. Границей элементов являются шарниры. Основные элементы могут работать (воспринимать нагрузку) без других. Второстепенные элементы опираются на другие. Более второстепенные элементы на поэтажной схеме показываются выше. В балках горизонтальная связь считается принадлежащей всем элементам.
2.Изображаем систему в расчлененном виде, раздвинув элементы. Показываем все нагрузки, опорные реакции и усилия взаимодействия в шарнирах. При этом сосредоточенные силы
могут быть приложены в шарнире. Сосредоточенный момент прикладывается около шарнира к левому элементу или правому, и это будут разные задачи.
3.Рассматривая равновесие каждого элемента, начиная с самого второстепенного, определяем опорные реакции и усилия взаимодействия в шарнирах. Если начать не с самого второстепенного элемента, то неизвестных будет больше, чем уравнений статики.
4.После определения опорных реакций и усилий взаимодействия
вшарнирах внутренние силовые факторы в сечениях любого элемента определяются как в отдельной простой балке.
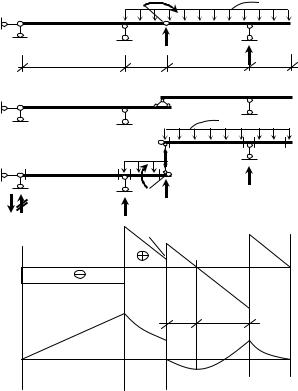
Пример 10.
Для балки, изображенной на
а) |
|
|
2ql 2 |
|
|
|
|
|
|
|
|
|
|
q |
|
||
|
|
|
|
|
|
|
|
|
A |
B |
|
|
C |
ql |
|
D |
E |
|
5l |
|
2l |
|
|
4l |
|
2l |
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
5 |
6 |
7 |
8 |
в) |
|
q |
|
VC=1,5ql |
|
|
||
1 |
2 |
3 |
|
4 |
|
|
||
|
|
|
|
|
||||
|
|
|
2ql |
2 |
ql |
|
VD=4,5ql |
|
VA=ql |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
VB=3,5ql |
|
|
|
||||
|
2,5 |
|
2 |
|
||||
г) |
|
|
0,5 |
|
1,5 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
ЭпQy |
1 |
|
|
|
|
|
|
|
(ql) |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
2,5 |
|
д) |
|
|
2 |
1,5l |
2,5l |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЭпMx |
|
|
|
|
|
|
|
|
(ql 2) |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
8 |
|
|
|
Рис. 49. Составная балка |
|
||||||
41
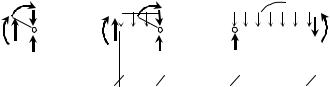
рис.49а, построить эпюры внутренних силовых факторов. Заданы: q и l .
Решение.
Данная балка состоит из двух элементов. Элемент C–D–E является второстепенным, так как без балки A–B–C балка C–D–E окажется на одной шарнирной опоре и не сможет воспринимать нагрузку. Элемент A–B–C основной, поскольку закреплен двумя шарнирными опорами. Отражаем это на поэтажной схеме (рис. 49б).
На рис. 49в показана заданная балка в расчлененном виде с действующими на нее силами. Обращаем внимание на то, что сосредоточенный момент приложен около шарнира к левому элементу. Силу q l можно было
приложить и к правому элементу. В шарнире С усилие взаимодействия показываем только вертикальное, так как из суммы проекций на горизонтальную ось для балки C–D–E очевидно, что горизонтальное усилие равно нулю.
Из условий равновесия балки C–D–E имеем:
momC = VD 4l − q 6l 3l = 0, |
VD |
= 9 ql; |
|
||
|
|
|
|
2 |
|
momD = VC 4l − q 6l l = 0, |
VC = |
3 ql. |
|
||
Проверка: V = 9ql + 3 ql − q 6l = 0 . |
|
2 |
|
||
|
|
|
|||
|
2 |
2 |
|
|
|
Опорные реакции для элемента C–D–E определены верно. |
|||||
Рассмотрим равновесие |
балки A–B–.С. |
|
|
|
|
momA = VB |
5l − q 2l 6l − 2ql2 − (3 ql − ql) 7l = 0, |
VB = 3,5ql; |
|||
|
|
2 |
|
|
|
momB = VA |
5l + q 2l l + 2ql2 + (3 ql − ql) 2l = 0, |
VA = −ql. |
|||
|
|
2 |
|
|
|
Величина VA |
получилась отрицательной. Это значит, что реакция VA |
||||
направлена не вверх, как было показано на рис. 49в, а вниз. Зачеркиваем первое обозначение VA , показываем новое направление вниз и указываем вели-
чину VA , опуская минус.
Проверка: |
V = −ql + 3,5ql − q 2l − 3 ql + ql = 0 . |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Опорные реакции для элемента A–B–С определены верно. |
|
|
|
|
||||||||||||||||||
Теперь эпюры Qy и |
4-4 |
|
|
|
3-3 |
|
|
|
|
|
6-6 |
|
|
|
||||||||
M X для каждого элемен- |
а) 2ql 2 |
1,5ql |
б) |
|
|
|
q |
2ql 2 |
в) |
q |
|
Mx,6-6 |
||||||||||
|
|
|
|
|
|
|
|
|
1,5ql |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
та можем |
построить как |
Mx,4-4 |
|
|
ql |
Mx,3-3 |
|
|
|
|
|
ql |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
для отдельной балки. С |
Qy,4-4 |
|
Qy,3- |
3 |
|
|
|
|
1,5ql |
|
|
Qy,6-6 |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
учетом накопленного уже |
|
|
|
|
|
|
|
|
|
|
2l |
|
|
|
|
|
4l |
|
|
|||
некоторого опыта эпюры |
Рис. 50. К определению усилий в сечениях |
|
|
|||||||||||||||||||
построим |
без |
лишних |
|
|
||||||||||||||||||
подробностей. |
|
|
|
|
|
|
|
|
составной балки |
|
|
|
|
|
|
|
||||||
42
Порядок рассмотрения элементов не имеет значения. Начнем с балки A–B–С. Все ординаты эпюр легко определить устно. Усилия в сечении 1–1
очевидны: |
Qy,1−1 = −ql, |
M X ,1−1 = 0. На участке 1–2 функция Qy (z) = const , |
M X (z) − |
линейная. |
M X ,2− 2 = −ql 5l = −5ql2 . Откладываем полученные |
ординаты на эпюрах (рис. 49г, 49д), проводим на эпюре Qy горизонтальную
линию, а на эпюре M X соединяем точки наклонной прямой.
На участке B–С удобнее начать определение усилий с сечения 4–4. Если есть необходимость, рассмотрим отсеченную часть на рис. 50а:
|
Qy,4− 4 = −ql + |
3 ql = |
1 ql, |
M X ,4− 4 = −2ql2 . |
|
При |
qY (z) = const |
2 |
2 |
|
|
на |
участке B–С функция |
Qy (z) − линейная, |
|||
M X (z) − |
квадратная |
парабола. Найдем в.с.ф. в сечении 3–3 (рис. 50б): |
|||
|
Qy,4− 4 = −ql + |
3 ql + q 2l = |
5 ql, M X ,3−3 = M X |
,2− 2 = −5ql2 . |
|
|
|
2 |
|
2 |
|
Откладываем ординаты на эпюрах, проводим установленные выше линии, на эпюре Qy ставим знаки и штрихуем графики. Обратим внимание, что
парабола на эпюре M X по «правилу паруса» имеет выпуклость вниз и каса-
тельная в сечении 4–4 не горизонтальна.
Для элемента C–D–E усилия в сечениях 5–5 и 8–8 определяются легко:
Qy,5−5 = |
3 ql, M X ,5−5 = 0 ; |
Qy,8−8 = 0, M X ,8−8 = 0 . |
|
2 |
|
На участках C–D |
и D–E qY (z) = const , |
функция Qy (z) − линейная, |
M X (z) − квадратная парабола. Внутренние силовые факторы в сечении 6–6
вычислим, рассматривая отсеченную часть на рис.50в:
Qy,5−5 = 32 ql − q 4l = − 52 ql, M X ,6−6 = 23 ql 4l − q 4l 2l = −ql2 .
В сечении 7–7 изгибающий момент уже известен, так как он не меняется при переходе от сечения 6–6 к сечению 7–7. Поперечная сила в сечении 7–7 из рассмотрения правой отсеченной части равна:
Qy,7− 7 = q 2l = 2ql . |
|
|
|
|
|
|
|
|
|
|
На участке C–D функция M X (z) |
имеет экстремум. Расстояние от шар- |
|||||||||
|
|
|
|
|
QY ,5−5 |
|
3ql |
|
3 l . |
|
нира С до сечения с экстремальным моментом равно |
|
= |
2 |
= |
||||||
|
|
q |
||||||||
|
|
|
|
|
|
q |
|
2 |
||
Вычисляем экстремум M X ,ЭКСТ = |
3 ql |
3 l − q |
3 l |
3 l = |
9 ql2 . |
|
|
|
||
|
2 |
2 |
2 |
4 |
|
8 |
|
|
|
|
Откладываем на эпюрах найденные ординаты, проводим прямые на эпюре Qy и параболы на эпюре M X ; на эпюре Qy ставим знаки и штрихуем
43
графики. Теперь очень полезно проделать все проверки (можно устно), которые обсуждались в предыдущем параграфе, чтобы убедиться в правильности решения и закрепить умение проверять эпюры.
8.ЭПЮРЫ ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ
ВПЛОСКИХ РАМАХ
Рамой называется брус, ось которого имеет ломаное очертание. Вертикальные элементы рамы называются стойками, горизонтальные – ригелями. Рама называется плоской, если оси всех стержней и нагрузка лежат в одной плоскости. В противном случае рама является пространственной.
В сечениях плоской рамы, очевидно, не равными нулю могут быть лишь те внутренние силовые факторы, которые действуют в плоскости рамы. Если продольная ось бруса обозначена «Z», а поперечная – «Y», то могут быть отличными от нуля продольная сила N, поперечная сила QY и изги-
бающий момент M X . Величины в.с.ф. определяются, естественно, методом
сечений.
При построении эпюр в рамах принятые ранее правила знаков для внутренних силовых факторов остаются без изменения. Аннулируется лишь правило знаков для изгибающего момента, так как для стоек им пользоваться неудобно. Да и необходимости в нем большой нет. Изгибающий момент показывается на эпюре со стороны растянутых волокон. Справедливы выведенные ранее дифференциальные зависимости для внутренних силовых факто-
ров: |
dN |
= −q (z), |
dQ |
= −q |
(z), |
dM |
X |
= Q (z), |
d 2M |
X |
= −q |
(z). |
||
|
Y |
|
|
|||||||||||
|
dz |
Z |
dz |
Y |
|
dz |
|
Y |
dz2 |
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
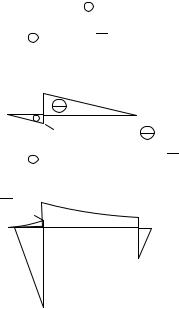
Пример 11. |
Для рамы, |
представленной на рис. 51, |
построить эпюры |
||||||||||
внутренних силовых факторов. Заданы: |
|
|
|
|
|
2q |
|
|||||||
q – параметр нагрузки, |
l – |
параметр |
|
|
3 4 5 |
|
|
6 |
|
|
||||
|
|
|
|
|
|
|||||||||
длины элементов рамы. Решение.
В шарнирно-неподвижной опоре A показываем две составляющих опорной реакции VA и H A . В шарнир-
но–подвижной опоре B может действовать только горизонтальная реакция HB . Без определения опорных реакций
3 |
|
2 |
2 |
67 |
7 |
|
|
K |
|
8 |
8 |
|
|
|
|
|
|
HA = |
ql |
1 |
1 |
|
|
VA = 162qll |
2l |
4l |
|
||
2l
HB = ql
3l
в.с.ф. определить нельзя. Для плоской |
Рис. 51. Плоская рама |
|
системы сил можно записать три неза- |
||
|
висимых уравнения равновесия. Их достаточно для определения трех опорных реакций. Уравнения записываем так, чтобы в каждое из них входила только одна искомая реакция (рис. 51).
44
V = VA − 2q 8l = 0, VA = 16ql;
momA = HB 3l + 2q 8l 2l = 0, |
HB |
= − |
32 ql; |
|
|
|
|
|
3 |
momK = HA 3l − 2q 8l 2l = 0, |
HB = |
32 ql . |
||
|
|
3 |
|
|
Для записи последнего уравнения использована вспомогательная точка K , которая позволяет исключить из уравнения уже найденные, но непроверенные реакции VA и HB . Знак минус в величине HB означает, что реакция
направлена не вправо, как предполагалось при записи уравнения, а влево. Показываем правильное направление HB , зачеркнув начальное, и проставля-
ем величины реакций (рис. 51). Для проверки реакций записываем уравне-
ние: |
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|||
H = 3 ql − |
3 |
ql = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
16 |
|
|
|
|
|
|
ЭпN( 3 |
|
|
|
|
|
|
||||||||
Разбиваем раму на участки. Их получается |
|
|
|
|
|
|
|
|
|
|
ql) |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
четыре, так как граница участков там, где меня- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ется конструкция или нагрузка. Соответственно |
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
необходимо найти в.с.ф. в восьми характерных |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
сечениях рамы. Для построения эпюр надо триж- |
|
|
|
|
|
|
|
|
|
|
|
ЭпQy(ql) |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ды повторить схему рамы без нагрузки и опор |
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
(рис. 52). |
|
|
|
|
|
|
|
|
|
|
57,3 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
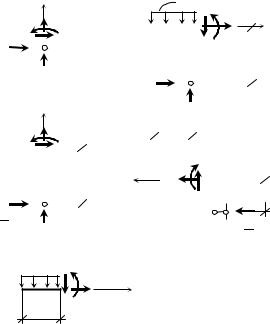
Определим усилия |
в |
сечении 1–1 (рис. |
в) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
21,3 |
|
||||||
53а): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
53,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
z = N1−1 + 16ql = 0, |
|
N1−1 = −16ql; |
|
|
|
|
|
|
|
|
|
|
|
ЭпMx(ql |
2 |
) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y = QY ,1−1 + 32 ql = |
|
QY ,1−1 = − 32 ql; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
|
3 |
Рис. 52. Эпюры в.с.ф. в пло- |
||||||||||||||||||||||
momX = M X ,1−1 = 0 . |
|||||||||||||||||||||||||
|
|
|
|
|
|
ской раме |
|
|
|
|
|
|
|||||||||||||
Величины этих усилий легко было определить и устно. Поскольку ни продольных, ни поперечных нагрузок на участке 1–2 не добавляется, то функции N (z) и QY (z) постоянны, а MX (z) – линейная функция. В сечении
2–2 (рис. 53б):
momX = M X ,2− 2 + 323 ql 5l = 0,
M X ,2− 2 = − 1603 ql2 = −53,3ql2 .
Знак «минус» в ответе означает, что изгибающий момент направлен не так, как показано на рис.53б, а наоборот и, следовательно, растягивает не правые волокна, а левые. Откладываем полученные ординаты на эпюрах перпендикулярно оси элемента 1–2 (рис. 52). Величины N(z) и QY (z) можно
45
|
|
|
1-1 |
|
|
|
|
|
|
|
|
|
|
5-5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а) |
|
|
|
z |
|
г) |
|
|
|
2q |
|
|
|
|
|
|
Mx,5-5 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|||||||||||||
|
M x,1-1 |
|
|
|
N1-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N5-5 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
1 Qy,1-1 |
|
|
|
|
|
|
|
|
|
|
|
Q y,5-5 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
ql |
16ql |
|
|
|
|
|
|
|
|
|
|
|
|
5l |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
б) |
2-2 |
|
|
|
|
|
|
|
|
|
ql |
16 |
ql |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
N2-2 |
|
|
|
|
|
2l |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
M x,2-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6-6 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Q y,2-2 |
|
|
|
|
|
|
|
|
д) |
|
|
|
Mx,6-6 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
5 |
l |
|
z |
|
|
|
N6-6 Q y,6- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
2l |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ql |
16ql |
ql |
|
||
|
|
|
4-4 |
|
|
|
2q |
Mx,4-4 |
|
в) |
|
z |
|
|
N4-4 |
||
|
2l |
|
|
|
Q y,4-4 |
|
|
|
|
|
Рис. 53. К определению усилий в плоской раме
отложить хоть слева, хоть справа, надо только поставить правильный знак. Изгибающий момент откладываем со стороны растянутых волокон, т.е. слева. Масштабы эпюр с разными размерностями независимы. На эпюрах N и QY ставим знаки и делаем штри-
ховку на всех трех эпюрах. Рассмотрим участок 3–4. В се-
чении 3–3 очевидно все в.с.ф. нулевые (из левой отсеченной части). В сечении 4–4 (рис. 53в) имеем:
z = N4− 4 = 0,
y = QY ,4− 4 + 2q 2l = 0,
QY ,4− 4 = −4ql;
momX = M X ,4− 4 |
+ 2q 2l l = 0, |
. |
M X ,4− 4 = −4ql2 |
|
|
|
|
Из дифференциальных зависимостей для участка 3–4 получаем: qZ (z) ≡ 0 N(z) = const,
q (z) = const Q (z) = M |
′ (z) − линейная M |
X |
(z) − квадратная парабола. |
|
Y |
Y |
X |
|
|
Откладываем ординаты на эпюрах в сечении 4–4, проводим линии, соответствующие указанным выше функциям (рис. 52).
Переходим к участку 5–6. Усилия в сечениях 5–5 и 4–4 разные, так как соответствуют совершенно разным отсеченным частям (независимо от того, левая часть рассматривается или правая). Для сечения 5–5 из левой отсеченной части (рис. 53г) получаем:
z = N5−5 + 32 ql |
= 0, N5−5 = − |
32 ql; |
|
3 |
|
3 |
|
y = QY ,5−5 + 2q 2l − 16ql = 0, |
QY ,5−5 = 8ql; |
||
momX = M X ,5−5 |
+ 2q 2l l + 32 ql 5l = 0, |
M X ,5−5 = −57,3ql2 . |
|
|
3 |
|
|
Характер линий на участке 5–6 такой же, как и на участке 3–4. Найдем усилия в сечении 6–6. Удобнее рассмотреть правую отсеченную часть (рис. 53д):
z = N6−6 |
+ |
32 ql |
= 0, N6−6 = − |
32 ql; |
Y = QY ,6− 6 = 0; |
||||
|
|
3 |
|
32 ql 2l = 0, |
3 |
|
|
64 ql2 |
|
momX = M X ,6−6 |
+ |
M X ,6−6 |
= − |
= −21,3ql2 . |
|||||
|
|
|
|
3 |
|
|
|
3 |
|
46
Откладываем ординаты по концам участка 5–6, проводим на эпюрах соответствующие линии (рис. 52). На эпюре M X в сечении 6–6 касательная
горизонтальна, так как QY ,6− 6 = 0 . |
|
а) |
4ql 12ql |
|
|
|
||||||
На участке 7–8 усилия определяются анало- |
4ql 2 |
57,3 ql 2 |
||||||||||
гично участку 1–2. Закончив построение эпюр, не- |
|
|
|
|
|
|
|
|
|
ql |
||
|
|
|
|
|
|
|
|
|
||||
обходимо сделать проверки. Проверку |
характера |
|
|
ql |
|
|
||||||
|
|
|
|
|||||||||
|
|
53,3 ql 2 |
||||||||||
|
|
|
|
|
|
|
|
|||||
линий, скачков, |
переломов, эпюры M X |
по площа- |
|
|
|
16ql |
|
|
|
|||
дям эпюры Q |
мы ранее уже обсуждали. Рассмот- |
б) |
|
|
|
|
||||||
Y |
|
|
4ql 2 |
|
|
|
|
|
57,3 ql 2 |
|||
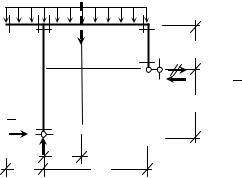
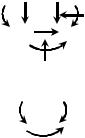
рим проверку равновесия узлов. В качестве примера |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
выделим узел сечениями 2–2, 4–4 и 5–5 (рис. 54а) и |
|
|
|
|
|
|
53,3 ql 2 |
|||||
покажем все действующие на него силы. Это внеш- |
|
|
|
|
|
|
|
|
|
|
||
ние силы, приложенные в узле (в данном примере их |
Рис. 54. Проверки равнове- |
|||||||||||
нет), и внутренние силовые факторы в сечениях, ве- |
|
|
сия узла |
|||||||||
личины которых с учетом знаков берем с эпюр. По- |
|
|
|
|
|
|
|
|
|
|
||
скольку узел должен находиться в равновесии, то можем записать три независимых уравнения равновесия. Например:
H = 323 ql − 323 ql = 0;
V = 16ql − 4ql − 12ql = 0;
momX = 53,3ql2 + 4ql2 − 57,3ql2 = 0 .
Условия равновесия выполняются. Поскольку чаще ошибки допускаются при построении эпюры изгибающих моментов, то можно отдельно проверить только изгибающие моменты. Для этого, вырезав узел, показываем все действующие на него моменты (рис. 54б) и записываем соответственно одно уравнение равновесия.
9.ЭПЮРЫ ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ
ВПРОСТРАНСТВЕННЫХ РАМАХ
Вэтом случае в каждом сечении надо определять все шесть внутренних силовых факторов. Они отражаются на четырех эпюрах, так как поперечные
силы QX и QY показываются на одной эпюре каждая в своей плоскости и изгибающие моменты M X и MY тоже. Правила знаков для в.с.ф. не меняются.
Чтобы не было разночтений при использовании правила знаков для поперечной силы, надо определиться с направлением взгляда. Поэтому рядом с рамой надо показать триаду осей и смотреть на соответствующую плоскость с острия перпендикулярной ей оси.
Справедливы все выведенные ранее дифференциальные зависимости для внутренних силовых факторов.
Рассмотрим построение эпюр в.с.ф. в пространственной раме на при-
мере.
47
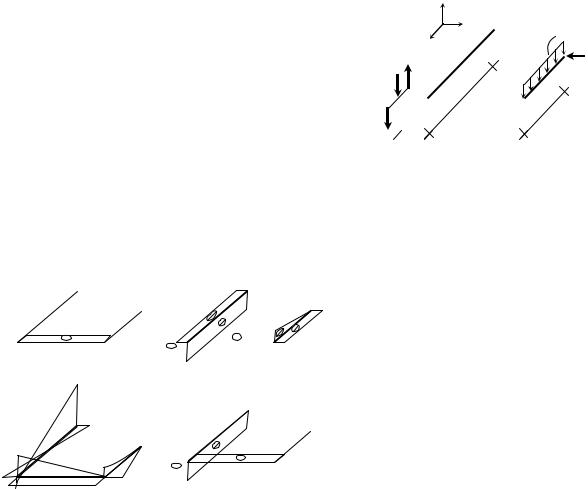
Пример 12. Для пространственной рамы, состоящей из взаимно перпендикулярных стержней (рис. 55), построить эпюры внутренних силовых факторов. Параметры нагрузки q и длины элементов l заданы.
Решение. |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В пространственной задаче в опоре в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
виде заделки необходимо определять шесть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
8 |
|
|
|
|
8 |
|
|
|
|
|
|||||||||
составляющих опорной реакции (три со- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2ql |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3ql |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ставляющих реактивной силы и три состав- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
6 |
5 |
|
7 |
7 |
|
5l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ляющих реактивного момента). Определе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
6 |
5 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3l |
|
|
|||||||||
ние опорных реакций в заделке совпадает с |
|
|
|
|
|
|
|
|
|
|
4l |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2ql 2 |
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
определением внутренних силовых факто- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ров в сечении рамы, примыкающем к за- |
|
|
|
Рис. 55. Пространственная |
|||||||||||||||||||||||||
делке. Начинать решение с вычисления |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
рама |
|
|
|
|
|
|
|
|
|
|
|||||||
опорных реакций нет необходимости, так |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
как для любого сечения можем рассмотреть отсеченную часть, свободную от опоры.
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
На эпюрах в данной раме |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
ЭпQ(ql) |
2 |
получается четыре участка и со- |
||||||||
|
|
|
|
ЭпN(ql) |
|
|
|
|
|
|
|
2 |
|
|
|
ответственно восемь характер- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ных сечений (рис. 55). Для по- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
строения |
эпюр |
четырежды |
по- |
||||
|
|
|
|
|
|
|
3 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вторяем |
схему |
рамы (рис. |
56). |
||
|
в) |
27,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
г) |
|
|
|
|
|
|
|
|
Рядом с рамой показываем триа- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
ЭпMt(ql 2) |
|
ду осей (рис. 55). |
|
|||||||||
|
|
|
|
ЭпMb(ql 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим в.с.ф. в сече- |
||||||
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4,5 |
|
|
|
|
|
||||||||
6 |
|
4,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нии 1–1, |
рассматривая отсечен- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
6 |
2 |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
ную часть на рис.57а. Внутрен- |
||||||||
6 |
3,5 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Рис. 56. Эпюры в.с.ф. |
|
|
|
|
|
|
|
|
ние силовые факторы N , QX , |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
в пространственной раме |
|
|
|
|
|
|
|
|
QY и MT |
показаны на схеме от- |
||||||||||||||||||
сеченной части положительными в соответствии с правилами знаков: продольная сила – растягивающая, поперечные силы вращают отсеченную часть по часовой стрелке. При этом на горизонтальную силу QX , действующую в
плоскости 1–3, надо смотреть сверху, т.е. с острия оси «2», а на вертикальную QY , действующую в плоскости 1–2, справа, т.е. с острия оси «3». Кру-
тящий момент MT направляем при взгляде со стороны отброшенной части (в
данном случае – спереди) против часовой стрелки. Изгибающие моменты M X и MY можно направлять произвольно, так как для них нет правила зна-
ков. Из условий равновесия видно, что в сечении 1–1 все в.с.ф. равны нулю
кроме QX : |
x = QX ,1−1 + 2ql = 0, |
QX ,1−1 |
= −2ql . |
На основании дифференциальных зависимостей определяем вид эпюр |
|||
на участке 1–2: |
N(z) = const , QX (z) = const , |
MY (z) − линейная, |
|
48
