
Эпюры ВСФ
.pdf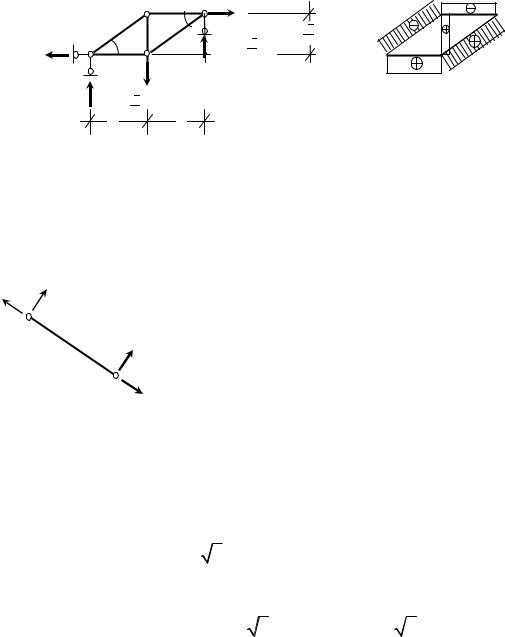
Эпюра N на участке 3–4 линейная, как и на участке 1–2. Откладываем на эпюре в сечении 4–4 полученную ординату 13γ Al и соединяем точку
прямой линией с ординатой в сечении 3–3. Указываем знаки N на каждом участке и штрихуем перпендикулярно оси эпюры.
Теперь можно показать опорную реакцию в заделке. Она равна величине N в сечении 4–4 (рис. 26а).
Пример 3. Построить эпюры внутренних силовых факторов для шар- нирно-стержневой системы, представленной на рис. 27а.
Дано: F – параметр нагрузки, угол α = 30 . |
|
|||||
|
|
2 |
3 |
F |
|
1.231 |
|
а) |
б) |
1.422 |
|||
|
α |
|
B |
|||
|
|
|
0.711 |
|||
|
|
|
√ l |
|||
F=HA |
1 |
α=30o |
|
VB=(1+√ )F= |
2.578 |
|
|
A |
4 |
K |
=1.289F |
|
|
|
|
|
|
|
||
|
2F |
|
|
|
2.231 |
|
|
|
|
|
|
||
|
VA=(1– √ )F=0.711F |
|
|
|
ЭпN(F) |
|
|
l |
l |
|
|
|
|
Рис. 27. Шарнирно-стержневая система
Решение.
Легко показать, что в брусе с шарнирами по концам и ненагруженном по длине (рис. 28), возникают лишь продольные силы. Из суммы моментов
HA |
|
относительно шарнира A следует, что со- |
VA |
|
ставляющая VB равна нулю. Аналогично рав- |
|
|
|
A |
|
но нулю VA из суммы моментов относитель- |
|
VB |
но шарнира B . Это значит, что стержень А–В |
B |
HB |
находится в равновесии лишь под действием |
|
продольных сил. Следовательно, для задан- |
|
|
|
|
Рис. 28. Стержень, нагруженный |
ной шарнирно–стержневой системы (рис. 27) |
|
в шарнирах на концах |
надо построить только эпюру продольных |
|
|
|
сил. |
Усилия в стержнях можно определить, рассматривая равновесие узлов. Предварительно необходимо найти опорные реакции. Обозначим длины горизонтальных элементов стержневой системы (рис.27а) через l . Тогда длина
стержня 2–4 равна l tg30 = |
3 |
l. Из условий равновесия всей системы (рис. |
|||||
3 |
|||||||
27а) имеем: |
|
|
|
|
|
||
|
|
|
|
|
|
||
momA = VB 2l − 2F l − F |
3 |
l = 0, VB = (1+ |
3 |
)F = 1,289F; |
|||
3 |
6 |
||||||
|
|
|
|
|
|||
19
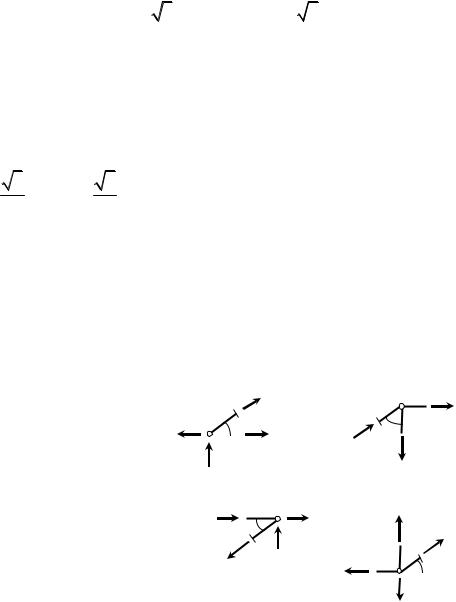
momK = VA 2l − 2F l + F |
3 |
l = 0, VA = (1− |
3 |
)F = 0,711F; |
|
3 |
6 |
||||
H = HA − F = 0, H A = F. |
|
|
|||
|
|
|
|
Для проверки правильности определения опорных реакций запишем сумму проекций всех сил на вертикаль (можно записать любое уравнение равновесия, которое не было использовано при определении опорных реакций):
V = (1+ 63 )F + (1− 63 )F − 2F = 0.
Опорные реакции найдены правильно и показаны на рис. 27а. Последовательно вырезая узлы, найдем усилия в стержнях. Рассмотрим
узел 1 (рис.29а). Искомые усилия показываем положительные, т.е. растягивающие.
|
|
V = N1− 2 |
sin 30 + 0,711F = 0, |
N1−2 = −1,422F; |
|
|
|
|
|
|
|
|
||||||||||
|
H = N1− 4 |
+ (−1,422F ) cos30 − F = 0, |
|
|
N1−4 = 2,231F. |
|
|
|
|
|
|
|
|
|||||||||
N1− 4 |
Для |
определения |
усилия |
а) |
|
|
|
|
N1-2 |
б) |
|
|
|
|
|
|
N2-3 |
|||||
можно было не использовать |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
N1-4 |
α=60o |
|||||||||||||||||
непроверенное пока N1− 2 , |
а запи- |
HA=F |
α=30o |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
сать |
для |
этого |
сумму проекций |
|
|
|
|
|
|
1.422F |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
сил |
на |
ось, |
перпендикулярную |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
VA=0.711F |
|
|
|
|
|
|
|
|
N2-4 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
стержню 1–2. |
|
|
|
|
в) |
1.231F |
F |
г) |
0.711F |
|||||||||||||
|
Откладываем |
полученные |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
α=30o |
|
|
|
|
|
|
|
|
|
1.578F |
||||||||||
значения |
на |
эпюре (перпендику- |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
VB=1.289F |
|
|
|
|
|
|
|
|
|
|
|||||||
лярно осям стержней), показываем |
|
|
N3-4 |
|
|
|
|
|
|
|
α=30o |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ординаты, знаки и штрихуем (рис. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
1.231F |
|
|
|
|
|
|
|
|
||||||||
27б). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2F |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
N1− 2 |
Вырезаем |
узел |
2. |
Усилие |
|
|
Рис. 29. Определение усилий в |
|||||||||||||||
показываем как известное с |
|
|
||||||||||||||||||||
учетом знака (рис. 29б). |
|
|
|
|
стержнях системы способом |
|||||||||||||||||
|
|
|
|
|
|
вырезания узлов |
||||||||||||||||
V = N2− 4 − 1,422F cos60 = 0, N2−4 = 0,711F;
H = N2−3 + 1,422F sin 60 = 0, N2−3 = −1,231F.
Дополним эпюру найденными усилиями (рис. 27б).
Рассмотрим узел 3 (рис. 29в). Усилие в стержне 3–4 легко найти из суммы проекций сил на вертикаль:
V = N3− 4 sin 30 − 1,289F = 0, N3−4 = 2,578F.
Показываем N3−4 на эпюре (рис. 27б). Все усилия найдены. Для про-
верки правильности решения можно для узла 3 записать сумму проекций сил на горизонталь:
20
H = 1,231F + F − 2,578F cos30 = F (1,231+ 1− 2,233) ≈ 0. |
|
||||||||
Ошибка в пределах точности вычислений. Окончательно в правильно- |
|||||||||
сти решения убедимся, рассмотрев узел 4 (рис. 29г), во всех стержнях кото- |
|||||||||
рого усилия уже известны: |
|
|
|
|
|
1 − 2) = 0, |
|
||
V = 0,711F + 2,578F sin 30 − 2F = F (0,711 + 2,578 |
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
H = 2,578F cos30 − 2,231F = F(2,578 |
3 |
− 2,231) = F(2,233 − 2,231) ≈ 0. |
|||||||
Задача решена верно. |
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|||
|
4. ЭПЮРЫ КРУТЯЩИХ МОМЕНТОВ |
|
|
||||||
Рассмотрим брус с прямолинейной осью, нагруженный только момен- |
|||||||||
тами относительно его продольной оси (рис. 30). Могут быть приложены и |
|||||||||
сосредоточенные моменты, и распределен- |
|
|
mz(z) |
|
|
||||
|
|
|
|
|
|||||
ный крутящий момент, интенсивность кото- |
|
|
|
|
|
||||
рого задается функцией mZ (z) . В этом слу- |
|
|
|
|
|
||||
чае в брусе |
возникают только крутящие мо- |
|
|
|
|
|
|||
менты. Брус, работающий на кручение, на- |
|
|
|
|
|
||||
зывается «вал». Величина крутящего момен- |
|
|
z |
dz |
|
||||
|
|
|
|
|
|||||
та определятся из условия равновесия левой |
|
|
Рис. 30. Вал |
|
|||||
или правой отсеченной части: |
|
|
|
|
|||||
M |
M |
|
momZ = 0, |
|
Mt |
= MZ = Ml,Z = Mr,Z . |
|||
|
|
|
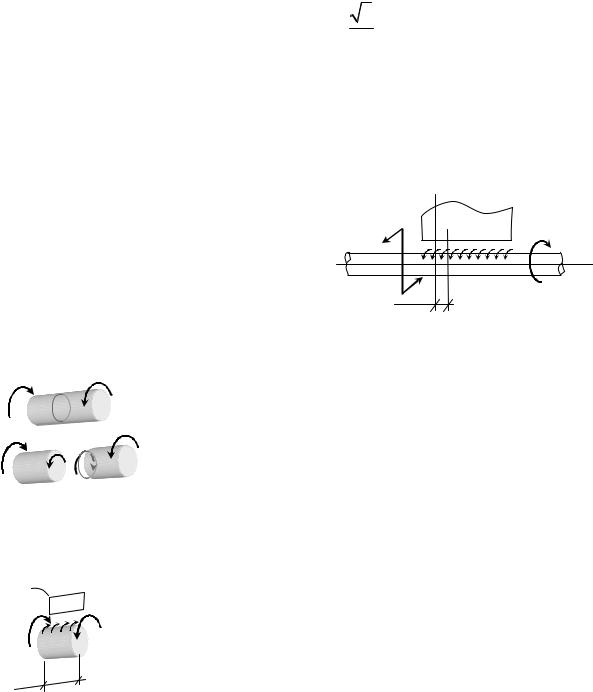
Примем правило знаков: крутящий |
||||||
M |
M |
|
момент считаем положительным, если при |
||||||
|
взгляде на сечение со стороны отброшенной |
||||||||
|
Mt>0 |
|
|||||||
|
|
|
части внутренний момент направлен против |
||||||
|
|
|
вращения часовой стрелки. Это правило от- |
||||||
Рис. 31. Правило знаков для крутя- |
ражено на рис. 31. Оба противоположно на- |
||||||||
правленные |
моменты взаимодействия M |
t |
|||||||
щего момента |
|
|
|
|
|
|
|||
|
|
|
положительны, так как вращают свою отсе- |
||||||
mz(z) |
|
ченную часть при соответствующем взгляде про- |
|||||||
|
тив |
часовой стрелки |
(на левый момент надо |
||||||
Mt |
Mt+dMt |
||||||||
смотреть справа, а на правый – слева). |
|
||||||||
|
|
||||||||
|
|
|
|||||||
|
|
|
Это правило формальное. Оно не содержит |
||||||
|
dz |
физического смысла и потому может быть раз- |
|||||||
z |
ным в разных учебниках. |
|
|
||||||
|
|
|
|||||||
Рис. 32. К выводу дифферен- |
|
Запишем дифференциальную зависимость |
|||||||
между внутренним крутящим моментом и на- |
|||||||||
циальной зависимости для |
|||||||||
крутящего момента |
грузкой. Для этого рассмотрим равновесие эле- |
||||||||
|
|
ментарного по длине |
участка |
вала (рис. 32). |
|||||
|
|
|
21 |
|
|
|
|
|
|
Подробности можно опустить, так как они обсуждались при выводе дифференциальной зависимости для продольной силы.
momZ = Mt − (Mt + dMt ) − mZ (z) dz = 0 .
После приведения подобных членов, переноса последнего слагаемого в правую часть и деления на dz получаем:
dMdzt = −mZ (z) ,
т.е. производная от крутящего момента по длине вала равна с минусом интенсивности распределенного крутящего момента.
Из этой зависимости можно сформулировать два следствия:
1)Порядок функции Mt (z) на единицу выше порядка функции mZ (z) .
2)Из дифференциальной зависимости можно выразить крутящий мо-
мент
Mt = − mZ (z) dz + c.
Здесь: c – постоянная интегрирования – величина крутящего момента в начале рассматриваемого участка;
интеграл – равнодействующий момент относительно продольной
оси бруса z от нагрузки на этом участке. |
|
|
|
|
|
|||
Все сказанное в этом пара- |
а) |
|
|
|
|
|
|
|
графе о крутящих моментах со- |
M1=3ml |
|
|
|
|
M1=5ml |
2ml |
|
вершенно аналогично тому, что |
|
|
3 |
2m |
4 |
|
|
|
написано в предыдущем пара- |
1 |
2 |
5 |
6 |
||||
|
|
|
||||||
графе о продольных силах. |
|
|
3 |
|
4 |
|
|
|
Пример 4. Построить эпю- |
1 |
2 |
|
5 |
6 |
|||
|
|
|
|
|||||
ры внутренних силовых факто- |
2l |
|
|
5l |
|
3l |
|
|
ров для бруса, изображенного на |
|
|
|
|
|
|
б) |
|
рис. 33а. |
в) |
|
|
|
|
7 |
|
|
Дано: l – параметр длины |
|
|
|
|
|
2 |
|
|
участков бруса, m – параметр |
|
|
|
|
|
|
||
|
|
|
|
|
|
ЭпMt(ml) |
||
нагрузки. |
|
|
|
|
|
|
|
|
На рис. 33а моменты изо- |
3 |
|
3 |
|
|
|
|
|
бражены на плоской проекции |
Рис. 33. Пример определения усилий |
|||||||
как пары сил. Сила представля- |
|
|
|
|
|
|
|
|
ется стрелой с «наконечиком» и |
в сечениях вала |
|
«хвостовым оперением» (рис. 33б). Если сила направлена к нам, то видим острие стрелы (кружок с точкой), если сила направлена от нас, то видим «хвостовое оперение» (кружок с крестиком).
Решение.
Поскольку опора одна, реакцию в заделке в начале решения определять не будем. Разбиваем брус на участки. Их получается три и, следовательно, необходимо найти величину Mt в шести сечениях (рис. 33а).
22
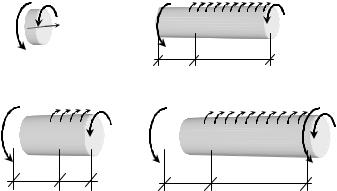
Для определения крутящего момента в сечении 1–1 рассмотрим соответствующую отсеченную часть, изображенную на рис. 34а. Искомый Mt
показываем положительный. Из условия равновесия имеем:
momZ = Mt,1−1 + 3ml = 0, Mt,1−1 = −3ml.
На участке 1–2 функция Mt (z) постоянна, так как производная от нее, равная – mZ (z) , нулевая. Откладываем величину крутящего момента в сече-
нии 1–1 на эпюре (рис. 33б), проводим постоянную линию до сечения 2–2 и указываем знак минус. Заштриховать эпюру можно как обычно или винтовой линией, чтобы выделить кручение.
В сечении 3–3 крутящий момент равен Mt в сечении 2–2, так как меж-
ду этими сечениями приложен лишь распределенный момент на бесконечно малом участке. Для построения эпюры на участке 3–4 надо найти величину Mt в сечении 4–4. Рассмотрим равновесие отсеченной части вала, представ-
ленной на рис. 34б:
momZ = 0, Mt,4− 4 = −3ml + 2m 5l = 7ml.
Откладываем полученное значение на эпюре и соединяем прямой с ординатой в сечении 3–3 (рис. 33б). Функция Mt (z) на участке 3–4 линейная,
так как на этом участке производная от нее, равная mZ (z) =const = 2m. Пока-
зываем знак и штриховку.
На участке 3–4 можно было построить эпюру Mt , получив для этого участка функцию Mt (z) . Рассматривая равновесие отсеченной части вала
(рис. 34в), имеем: |
а) |
1 – 1 |
|
б) |
|
momZ = 0, |
3ml |
3ml |
2m |
||
Mt,1-1 |
|||||
Mt,4-4 |
|||||
|
|
|
|
||
Mt (z) = –3ml + 2m z. |
|
z |
|
|
|
Получили |
линейную |
|
|
2l |
5l |
|
||
функцию. |
Подставив в нее |
в) |
2m |
г) |
2m |
|
|||
z = 0 |
и |
z = 5l , |
вычислим |
3ml |
3ml |
5ml |
|||
|
|
|
|
|
|
|
|
|
|
величины |
крутящего |
мо- |
|
|
|
|
Mt,5-5 |
||
мента в сечениях 3–3 и 4–4. |
|
|
Mt,(z) |
|
|
||||
|
В сечении 5–5 найдем |
2l |
z |
2l |
5l |
|
|||
крутящий момент, рассмат- |
|
||||||||
|
|
|
|
|
|||||
ривая отсеченную часть на |
|
Рис. 34. Определение крутящего момента |
|||||||
рис. 34г. |
|
|
|
|
|||||
|
|
|
|
|
в сечениях вала |
|
|||
Mt,5−5 = −3ml + 2m 5l − 5ml = 2ml.
Откладываем ординату на эпюре (рис. 34г) и проводим постоянную линию (аналогично участку 1–2). Из эпюры видно, что реактивный момент в заделке равен 2ml . Направление реакции устанавливаем по знаку крутящего момента в сечении 4–4.
23
5. ЭПЮРЫ ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ В БАЛКАХ
Балкой называется брус, работающий на изгиб.
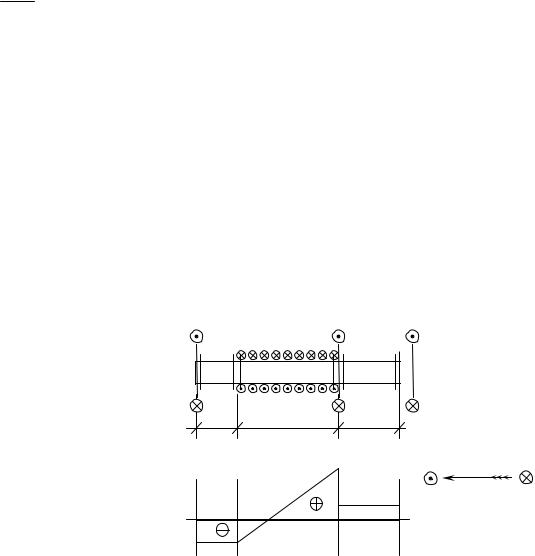
Если имеем брус с прямолинейной осью, к которому приложены только силы, которые перпендикулярны оси и пересекают эту ось, то в поперечных сечениях бруса отличными от нуля будут четыре внутренних силовых
фактора: M X , MY , QX , QY .
Для определения внутренних усилий удобно разложить заданную на-
грузку по главным плоскостям бруса |
|
|
qy(z) |
|||||
и определять в.с.ф. в каждой из этих |
|
|
||||||
y |
|
|
|
|||||
|
||||||||
плоскостей независимо друг от дру- |
|
|
|
|
|
|
|
|
га. Главными называются плоскости, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проходящие через продольную ось |
|
|
|
|
|
|
|
z |
бруса и одну из главных централь- |
|
|
z |
|
|
|
|
|
|
|
|
|
dz |
||||
ных осей поперечного сечения. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим брус с прямоли- |
Рис. 35. Балка, нагруженная в плоскости zy |
|||||||
нейной осью и нагруженный в плос- |
|
|
|
|
|
|
|
|
кости ZY (рис. 35). Нагрузка может быть приложена в виде сосредоточенных сил, сосредоточенных моментов, а также в виде поперечной нагрузки, распределенной по длине бруса. Величина интенсивности распределенной нагрузки задается функцией qY (z) .
При нагружении в плоскости ZY в поперечных сечениях балки могут быть отличными от нуля изгибающий момент M X и поперечная сила QY .
Они определяются из условий равновесия отсеченной части:
momX = 0, |
M X = Ml, X = Mr, X ; |
|
||||||||||||
Y = 0, |
Qy = Fl, y = Fr, y . |
|
|
|
|
|
|
|
|
|
|
|
||
Введем правила знаков. Попе- |
а) |
|
|
|
|
|
б) |
|
||||||
речную силу Q считаем положитель- |
F |
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ной, если она вращает |
отсеченную |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Mx |
|
|
|
Mx |
|||
часть по часовой стрелке (рис. 36а). |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
F |
|
|
|
|
|
|
F |
|
||||||
Это же правило можно сформулиро- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вать так: Q больше нуля, если она на- |
|
|
|
|
Qy>0 |
|
||||||||
правлена справа от сечения вниз, а |
|
|
Рис. 36. Правила знаков для |
|
||||||||||
слева от сечения – вверх. |
|
|
|
|
|
|
в.с.ф. в балках |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Изгибающий момент M X положительный, если вызывает растяжение
нижних волокон балки (рис. 36б). При этом на эпюре положительный момент откладывается вниз, т.е. со стороны растянутых волокон*.
* Машиностроители, используя для изгибающего момента такое же правило знаков, откладывают на эпюре положительный момент вверх, т. е. строят эпюру на сжатых волокнах. Это различие сложилось исторически. Первыми эпюры начинали строить именно строители и строили их как «веревочные многоугольники». Оказывается, что нить, загруженная поперечной нагрузкой, прила-
24

Получим для балок дифференциальные зависимости, связывающие внутренние силовые факторы с нагрузкой. Рассмотрим равновесие бесконечно малого по длине участка балки (рис. 37), выделенного из бруса (рис. 35). Усилия
на рис. 37 показаны положительные. Так как аргумент z получил приращение |
|||||||
|
qy(z) |
|
|
|
dz , то и функции Qy (z) и MX (z) получают со- |
||
|
|
|
|
ответственно приращения dQy и dMX . |
|||
|
|
|
|
|
|||
|
Mx |
|
|
Mx+dMx |
|
|
Y = Qy − (Qy + dQy ) − qy (z) dz = 0. |
|
Qy |
|
|
Qy+dQy |
|
|
Приводим подобные члены, переносим |
|
z |
dz |
|
последнее слагаемое в правую часть и делим |
|||
|
|
|
|||||
|
|
|
|
||||
|
|
|
|
|
выражение на dz . Получаем: |
||
|
|
|
|
|
|||
Рис. 37. К выводу дифференциаль- |
|
dQy |
= −qy (z) , |
||||
ных зависимостей для балок |
|
|
|||||
|
dz |
||||||
|
|
|
|
|
|
|
|
т.е. производная от поперечной силы по длине балки равна с минусом интенсивности поперечной распределенной нагрузки. Отсюда знакомые уже по виду следствия:
1)Порядок функции Qy (z) на единицу выше порядка функции qY (z) .
2)Из дифференциальной зависимости можно выразить Qy (z) :
Qy = − qy (z) dz + c ,
т.е. поперечная сила в конце участка равна значению ее в начале участка « c » плюс (в алгебраическом смысле) равнодействующая поперечной нагрузки на этом участке.
Запишем для выделенного элемента (рис. 37) сумму моментов относительно оси x , которую удобнее взять в правом сечении:
momX = M X − (M X + dM X ) + Qy dz − qy (z) dz dz2 = 0 .
После приведения подобных остается три слагаемых:
−dM X + Qy dz − qy (z) dz dz2 = 0 .
При этом первые два слагаемых являются бесконечно малыми первого порядка. Третье слагаемое представляет собой произведение дифференциалов и, следовательно, является величиной второго порядка малости и потому им можно пренебречь. Тогда остается:
−dM X + Qy dz = 0 .
Получаем: dM X = Qy (z) , dz
гаемой к балке, принимает форму, совпадающую с эпюрой изгибающих моментов. При этом нить прогибается, естественно, в направлении действия нагрузки, т.е. в сторону растянутых волокон. У проектировщиков-строителей сохранился именно этот вариант, так как основным строительным материалом является бетон, который на растяжение практически не работает. Поэтому с той стороны, где отложен на эпюре изгибающий момент, надо проектировать армирование.
25
т.е. производная от функции изгибающего момента по длине балки равна поперечной силе. Сформулируем соответствующие этой зависимости два следствия:
1)Порядок функции MX (z) на единицу выше порядка функции Qy (z) .
2)Изгибающий момент можно выразить из дифференциальной зависи-
мости:
M X = Qy (z) dz + c .
Учитывая геометрический смысл определенного интеграла, это значит, что разность между изгибающими моментами в начале и в конце участка равна площади эпюры поперечных сил на этом участке.
Как следствие двух, полученных выше, дифференциальных зависимостей для балок можно получить третью дифференциальную зависимость. Поскольку производная от изгибающего момента равна поперечной силе, а производная от поперечной силы равна интенсивности поперечной распределенной нагрузки (с минусом), то «- qy (z) » является второй производной от M X :
d 2M X = −qy (z). dz2
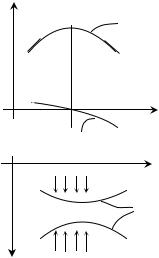
Эта зависимость позволяет доказать, что выпуклость кривой на эпюре MX (z) совпадает по направлению с распределенной нагрузкой («правило пару-
са»). Легко показать, что для любой кривой, выпуклость которой совпадает с положительным направлением оси (рис. 38а), вторая производная отрицательна. На рис. 38а видно, что для такой кривой значения первой производной меняются с плюса через ноль на минус, т.е. функция y′(x) убывающая, а значит
y′′ = (y′)′ < 0 . Теперь можем показать, что при распределенной нагрузке, направленной вниз, выпуклость кривой MX (z) направлена вниз (в положитель-
ную сторону оси), так как при этом qy (z) |
по- |
y |
|
||||
|
′′ |
|
а) |
|
|||
|
|
|
|
|
|
||
ложительна, а значит (M X (z)) |
отрицательна |
y'>0 |
y'=0 |
y(x) |
|||
(рис. 38б). Если нагрузка направлена вверх, то |
|
|
y'<0 |
||||
|
|
|
|||||
′′ |
положительна и, |
|
|
|
|
||
qy отрицательна, (M X (z)) |
|
|
|
|
|||
следовательно, выпуклость |
кривой M X |
на- |
|
|
|
z |
|
правлена в сторону, обратную положительному
направлению оси M X , т.е. вверх. |
|
y'(x) |
|
|
z |
||
Рассмотрим примеры построения эпюр б) |
|
qy>0, Mx’’<0 |
|
внутренних силовых факторов в балках. |
|
|
|
Пример 5. Для балки, показанной на |
|
Mx |
|
|
|
||
рис. 39а, необходимо построить эпюры внут- |
Mx |
qy<0, Mx’’>0 |
|
ренних силовых факторов. |
|||
|
|
Рис. 38. Обоснование "правила паруса"
26
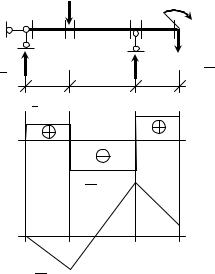
Заданы: |
F – параметр нагрузки, |
|
|
|
|
|
|
|
|
|
|
l – параметр длины участков балки. |
|
|
|
|
|
|
|
||
Решение. |
|
|
|
|
|
|
|
|
|
|
Эпюры в.с.ф. для этой балки без определения опорных реакций по- |
||||||||||
строить невозможно, так как для сечений в пролете опорные реакции будут |
||||||||||
входить в условия равновесия и для левой, и для правой отсеченной части. |
||||||||||
При этом внутренние усилия в сечениях на консоли можно вычислить и не |
||||||||||
зная опорных реакций. |
|
|
|
|
|
|
|
|
|
|
Обозначим опоры буквами A и B , |
возникающие в них вертикальные |
|||||||||
реакции VA и VB . Горизонтальную реакцию в шарнирно–неподвижной опоре |
||||||||||
A обозначим H A . |
|
|
|
|
|
|
|
|
|
|
Для плоской системы сил можно записать три независимых уравнения |
||||||||||
равновесия и соответственно найти все три реакции. Здесь и далее будем по |
||||||||||
возможности записывать уравнения с одним неизвестным, не используя най- |
||||||||||
денные, но не проверенные усилия. |
|
|
|
|
|
|
|
|
||
В рассматриваемом примере имеем: |
|
|
|
|
|
|
|
|
||
H = HA = 0; |
|
|
|
|
|
|
|
|
|
|
momA = VB 5l − 4F 2l − 2F 7l − Fl = 0, |
VB = |
23 F |
; |
|
|
|
|
|
||
|
|
|
|
5 |
|
|
|
|
|
|
momB = VA 5l − 4F 3l + 2F 2l + Fl = 0, |
VA = |
7 F . |
|
|
|
|
|
|||
Впредь в балках, нагруженных |
|
5 |
|
|
|
|
|
|
||
|
4F |
|
|
|
|
M=Fl |
||||
только вертикальной нагрузкой, можно |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
||
горизонтальную реакцию не определять, |
A |
1 |
2 |
3 |
4 |
5 |
6 |
2F |
||
понимая по умолчанию, что она равна ну- |
VA= F |
|
|
|
B |
|
|
VA= F |
||
2l |
|
3l |
|
|
2l |
|||||
лю. Показываем величины найденных ре- |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
акций (рис. 39 а). |
|
|
|
|
|
|
|
2 |
|
|
Определение опорных реакций обя- |
|
F |
|
|
|
|
|
ЭпQy(F) |
||
зательно должно завершаться проверкой. |
|
|
|
|
|
|
|
|
||
Для этого записывается любое из бесчис- |
|
|
|
|
|
5 |
|
|||
ленного множества возможных уравнение |
|
|
|
|
|
|
||||
|
|
|
F |
|
|
|
|
|||
равновесия, которое не было использова- |
|
|
|
|
|
|
1 |
|||
|
|
|
|
|
|
|
||||
но при определении опорных реакций. |
|
|
|
|
|
|
|
ЭпMx(Fl) |
||
|
|
|
|
|
|
|
|
|||
Удобнее всего записать сумму проекций |
|
|
|
|
|
|
|
|
||
всех сил на вертикаль: |
|
|
F |
|
|
|
|
|
|
|
V = 7F − 4F + |
23 F − 2F = 0 . |
|
|
|
|
|
|
|
||
|
Рис. 39. Эпюры в.с.ф. в балке |
|||||||||
|
5 |
5 |
|
|
|
|
|
|
|
|
Опорные реакции найдены правильно. Правда, если сосредоточенный |
||||||||||
момент в обеих суммах моментов записан с неправильным знаком, то эта |
||||||||||
проверка ошибку не обнаружит. Просто реакции будут вычислены для дру- |
||||||||||
гой нагрузки. |
|
|
|
|
|
|
|
|
|
|
27
Разбиваем балку на участки. Их получается три. Это значит, что в.с.ф. надо вычислить в шести сечениях, взятых бесконечно близко к границам участков. Методом сечений определяем внутренние силовые факторы в указанных сечениях. При этом в каждом случае берем удобную отсеченную часть.
Найдем усилия в сечении 1–1, рассматривая левую отсеченную часть (рис.40а). Искомые QY и M X показываем положительные.
Y = Qy,1−1 − |
7 F = 0, |
Qy,1−1 = |
7 F; |
|
5 |
|
5 |
M X ,1−1 = 0
На конце бруса внутренний момент всегда равен нулю, если не приложен сосредоточенный момент, так как любые другие нагрузки имеют нулевое плечо.
По длине |
участка 1–2 |
q (z) ≡0. Так |
|
как |
Q ′(z) ≡ 0 |
, то |
||
|
′(z) |
|
Y |
|
|
|
y |
|
Q (z) = const = M |
и следовательно функция M |
X |
(z) |
линейная. Эти рас- |
||||
y |
X |
|
|
|
|
|
|
|
суждения справедливы и для участков 3–4 и 5–6. На участке 1–2 это можно показать, записав выражение для M X из условия равновесия отсеченной
части, представленной на рис. 40б:
momX = M X (z) − |
7 F z = 0, |
M X (z) = |
7 F z . |
|
5 |
|
5 |
Функция MX (z) получилась линейной. Ординаты эпюры в сечениях
1–1 и 2–2 вычисляются подстановкой значений z = 0 и z = 2l . Положительные значения M X , как уже было сказано, откладываем вниз, т.е. со стороны
растянутых волокон.
Аналогично запишем функцию MX (z) на участке 3–4, рассматривая
равновесие левой отсеченной части балки (рис. 40в) или правой (рис. 40г). Из условия равновесия левой отсеченной части (рис. 40в) имеем:
Y = Qy (z) − |
7 F + 4F = 0, Qy (z) = − |
13 F; |
|
|
5 |
5 |
|
momX = M X (z) − |
7 F z + 4F (z − 2l) = 0, |
M X (z) = − |
13 F z + 8Fl. |
|
5 |
|
5 |
Из условия равновесия правой отсеченной части (рис. 40г) получается:
Y = Qy (z) + |
23 F − 2F = |
0, |
Qy (z) |
= − |
13 F; |
|
|
5 |
|
|
|
5 |
23 F (5l − z) = 0, |
momX = M X (z) + Fl + 2F (2l + (5l − z)) − |
||||||
|
|
|
|
|
|
5 |
28
