Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Южно-Уральский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Эпюры ВСФ

.pdf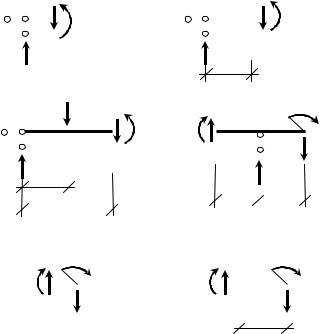

Скачиваний:

Добавлен:

09.05.2015

Размер:

1.38 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

M X (z) = − 135 F z + 8Fl.

Результаты, естественно, совпадают. Рассматривая правую отсеченную часть удобнее было бы взять

другое начало координат.	а)	1–1	Mx,1–1	б)	Mx(z)

Для поперечной силы

получили

Qy,1–1

Qy(z)=

Qy (z) = const = − 13 F.

VA= F

Mx(z)

Для

изгибающего

мо-

в)

г)

мента функция MX (z) полу-

чилась

линейной.

Подставив

Qy(z)

координаты

третьего и

чет-

5l- z

вертого сечений, получим:

M X ,3−3

= −

F 2l + 8Fl =

Fl,

д)

6–6

е)

5–5

Mx(z)

M X ,4−4

= −

F 5l + 8Fl = 3Fl .

Откладываем

получен-

Рис. 40. К определению усилий

ные ординаты на

эпюрах в

в сечениях балки

сечениях 3–3 и 4–4 и соединя-

ем точки прямыми линиями (рис. 39б, в), на эпюре QY

ставим знак, делаем

штриховку.

Для построения эпюр на консоли удобнее рассматривать правую отсеченную часть. Характер эпюр на этом участке уже определен. Величины усилий можно найти, записав функции Qy (z) и MX (z) на участке 5–6, или вы-

числить конкретно усилия в сечениях 5–5 и 6–6.

При построении эпюр внутренних силовых факторов изображать отсеченные части и записывать уравнения равновесия надо до тех пор, пока в этом есть необходимость. Имея достаточный опыт, большинство ответов можно получить устно.

Рассмотрим сечение 6–6 (рис. 40д):

Y = Qy,6−6 − 2F = 0, Qy,6−6 = 2F;
momX = M X ,6−6	+ Fl = 0,	M X ,6−6 = −Fl.
Для сечения 5–5 (рис. 40е) поперечная сила уже известна, а изгибаю-
щий момент находим:
momX = M X ,5−5	+ Fl + 2F 2l = 0,		M X ,5−5 = −5Fl.

Показываем эпюры QY и M X на последнем участке.

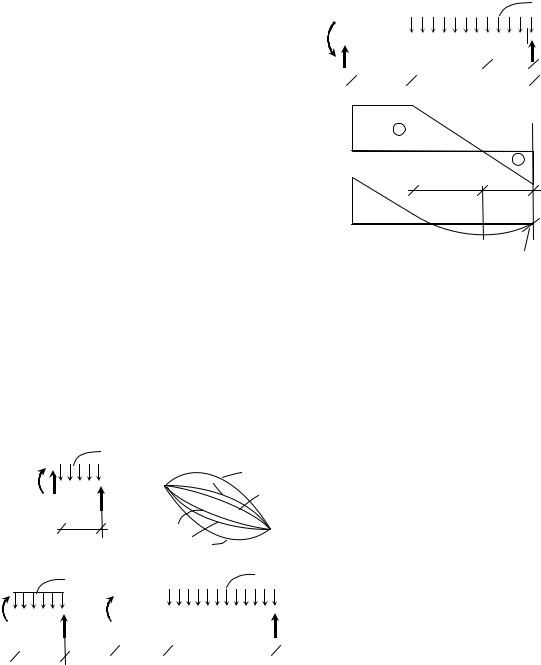
Пример 6. Для консольной балки, показанной на рис. 41а, требуется построить эпюры внутренних силовых факторов.

Заданы: q – параметр нагрузки,

l – параметр длины участков балки.

Решение.

Учитывая, что опора одна, начинать решение с определения опорных реакций не будем. Разбиваем балку на два участка. Можно устно определить внутренние усилия в сечениях 1–1 и 2–2. Если это затруднительно, запишем

функции Qy (z)

и MX (z), рассматри-

а)

вая равновесие

отсеченной

части

18ql 2

балки, представленной на рис. 42а.

z 1

5ql

Y = QY (z) + 5ql − 3q z = 0,

7ql

QY (z) = 3q z − 5ql;

б)

momX = M X (z) − 5ql z + 3q z

= 0,

ЭпQy(ql)

M X (z) = 5ql

z − 2 q z2.

в) 18

= F

Видим, что на участке 1–2

ЭпMx(ql2)

функция Qy (z)

линейная, а MX (z) –

M'x=-5ql

квадратная парабола. Это можно ус-

Рис. 41. Эпюры в.с.ф. в консоль-

тановить и используя дифференци-

альные зависимости:

ной балке

q (z) = const = Q ′(z) Q (z) = M

′(z) − линейная M

(z)

− кв. парабола.

Подставляя в функции Qy (z) и MX (z) координаты сечений 1–1 и 2–2

( z = 0 и z = 4l ), получим

Qy,1−1 = −5ql, Qy,2− 2 = 7ql , M X ,1−1 = 0, M X ,2= 2 = −4ql2 .

а)

Mx(z)

б)

-4ql 2

Qy(z)

5ql

5–5

4–4

в)

г)

5ql

Mx,ЭКС

5ql

Рис. 42. К определению усилий в сечениях консольной балки

Откладываем найденные значения на эпюрах. На эпюре QY по-

лученные точки соединяем прямой линией, ставим знаки и делаем штриховку. На эпюре MX (z) надо

показать квадратную параболу. Из шести вариантов, представленных на рис. 42б, первые три противоречат «правилу паруса». Три другие отличаются положением касательной в точке, соответствующей сечению 1–1. Правильное положение касательной можно установить, ис-

пользуя первую производную от функции MX (z):

M X ′(z)1−1 = Qy (z)1−1 = −5ql .

Учитывая положительное направление осей z (вправо) и M X (вниз) по-

казываем ориентировочное положение касательной, которая указывает на правильность шестого варианта параболы. Этот же вариант параболы «напрашивается» из условия экстремальности M X в сечении, которому соответ-

ствует QY , равное нулю.

Для завершения эпюры M X на участке 1–2 необходимо вычислить экстремальное значение M X . Во-первых, найдем положение сечения с экстремальным моментом. Координату z0 (рис. 41б) можно найти тремя спосо-

бами.

1. Рассмотреть подобие треугольников. Это наиболее громоздкий вариант. Кроме того, он возможен только в том случае, когда функция Qy (z)

линейная.

2. Записать функцию Qy (z) и, приравняв ее нулю, вычислить z0 . Этот вариант решения может быть использован при любой функции Qy (z) . В рассматриваемом примере эта функция уже записана. Получаем:

Q	(z) = 3q z − 5ql = 0,	z	0	= 5 l .
Y	0		0	3
				3

3. Для участка с равномерно распределенной поперечной нагрузкой вместо рассмотрения подобия треугольников величину z0 можно легко опреде-

лить устно. Поперечная сила будет равна нулю там, где QY , действующая на конце участка, уравновесится распределенной нагрузкой. Поэтому z0 = Qqy .

В данном примере от правого конца участка 1–2 z0 = 53qlq = 53 l .

От сечения 2–2 расстояние z0 = 73qlq = 73 l . Для проверки можно убедить-

ся, что 73 l + 53 l = 4l , т.е. совпадает с длиной участка 1–2.

Величину экстремального момента, имея функцию MX (z), можно вы-

числить, подставив z = 53 l .

M X ,ЭКС = 5ql 53l − 32 q (53 l)2 = 256 ql2 .

Эту же ординату получим, рассматривая отсеченную часть для сечения

5–5 (рис. 42в):

= M X ,5−5 = 5ql 5 l − 3q

5 l

25 ql2 .

M X ,ЭКС

Теперь, наконец, через три точки (в сечениях 1–1, 5–5 и 2–2) можно

провести квадратную параболу и заштриховать эпюру.

На участке 3–4:

q (z) ≡ 0 = Q ′

(z) Q (z) = M

′(z) = const M

(z)

− линейная.

В сечении 3–3 усилия такие же, как и в сечении 2–2, так как расстояние

между ними равно нулю и никаких сил не добавляется. Внутренние силовые

факторы в сечении 4–4 можно вычислить, записав функции Qy (z)

и MX (z)

на этом участке. Но проще, поскольку характер эпюр уже известен, рассмот-

реть отсеченную часть для сечения 4–4 (рис. 42г):

M X ,4− 4 = 5ql 6l − 3q 4l (2l + 2l) = −18ql2 .

Откладываем ординаты на эпюрах, проводим постоянную линию на

эпюре QY

(рис. 41б) и линейно переменную на эпюре M X

(рис. 41в). Закан-

чиваем штриховку эпюр. Показываем опорные реакции в защемлении (рис.

41а), понимая, что они равны в.с.ф. в сечении 4–4.

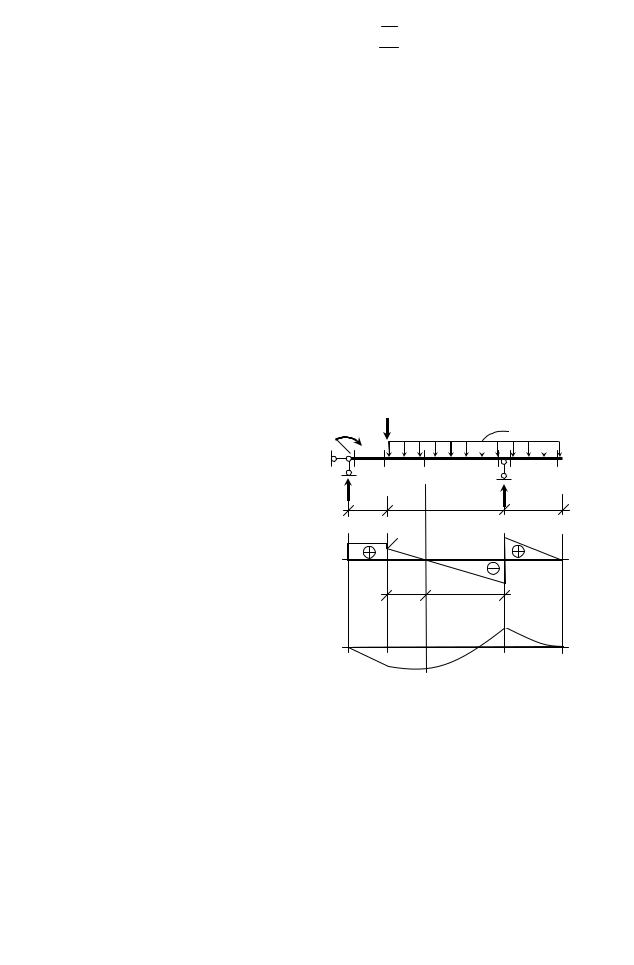
Пример 7. Для

балки,

изо-

a) ql 2

браженной на рис.

43а, построить

эпюры внутренних силовых факто-

ров.

VA=4ql

Заданы:

VB=15ql

– параметр длины участков

балки,

б)

ЭпQy(ql)

q – параметр нагрузки.

Решение.

1,5l

4,5l

В этой задаче без определе-

ния опорных реакций не обойтись.

в)

)

Горизонтальная составляющая

ре-

ЭпMx(ql

акции

шарнирно–неподвижной

11,25

опоре

как уже обсуждалось вы-

Рис. 43. Эпюры в.с.ф. в однопролетной

ше, равна нулю. Найдем вертикаль-

ные реакции VA и VB .

балке с консолью

momA = VB 8l − ql2 − ql 2l − 2q 9l (2l + 4,5l) = 0,

VB = 15ql;

momB = VA 8l + ql2− ql 6l − 2q 9l 1,5l = 0,

VA = 4ql .

Проверка опорных реакций:

V = 4ql − ql − 2q 9l + 15ql = 0 .

Реакции найдены правильно. Сомнения могут быть связаны лишь со

а)

2–2

б) Mx(z)

знаками

момента ql2 в

обоих

Mx,2-2

уравнениях.

Qy(z)

Разбиваем балку на участки.

Qy,2-

Их получается три и соответствен-

15ql

но

шесть

характерных

сечений

6–6

ql 2

(начало и конец каждого участка).

в)

г)

Mx,6-6

Построение

эпюр можно

начать

хоть с левого конца, хоть с право-

Mx,экс

Qy,6-6

го. В сечении 1–1, т.е. на правом

15ql

конце балки, очевидно, что QY и

4,5l

VA=4ql

M X

равны нулю, так здесь нет ни

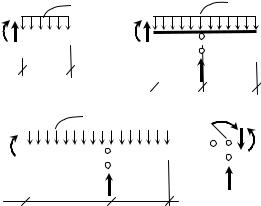
Рис. 44. К определению усилий в сечениях

сосредоточенных сил, ни сосредо-

однопролетной балки с консолью

точенных моментов. В сечении 2–2

= −2q 3l 3l

(рис. 44а) получаем:

− 2

= 2q 3l

= 6ql, M

X ,2− 2

= −9ql2 .

Y ,2

Напомним, что в уравнениях равновесия правило знаков одно: силы (или моменты), направленные в одну сторону, берутся с одним знаком (любым). При переносе слагаемых в правую часть усилие, совпадающее по направлению с искомым в.с.ф., пойдет с минусом.

Откладываем ординаты на эпюрах (рис. 43б, 43в). Положительное QY откладываем вверх и отрицательное M X тоже вверх. Характер функций устанавливаем, используя дифференциальные зависимости:

qY (z) = const = Qy′(z) QY (z) = M X ′(z) − линейная M X (z) − кв.парабола.

На эпюре QY соединяем точки прямой линией, на эпюре M X показы-

ваем параболу выпуклостью вниз (по «правилу паруса»). При этом надо убедиться, что касательная на эпюре M X в сечении 1–1 горизонтальна, так как

′	= 0 .
M X ,1−1 = QY ,1−1
Далее можно аналогично рассмотреть сечения 3–3 и 4–4 или записать
функции Qy (z) и MX (z) на участке 3–4 (рис. 44б):
Y = 0,		Qy (z) = 2q z −15ql;
momX	= 0,	M X (z) = 15ql (z − 3l) − 2q z			z	= −q z2	+ 15ql (z − 3l) .

				2
Получили линейную функцию Qy (z) и квадратную параболу MX (z).
Сечению 3–3 соответствует z = 3l,				QY ,3−3 = 2q 3l − 15ql = −9ql;
M X ,3−3 = M X ,2− 2 = −9ql2 .
В сечении 4–4 z = 9l,			QY ,4− 4 = 2q 9l − 15ql = 3ql;

M X ,4− 4 = −q (9l)2 + 15ql (9l − 3l) = 9ql2 .

Откладываем полученные ординаты в сечениях 3–3 и 4–4. На эпюре QY соединяем точки прямой линией, ставим знаки и штрихуем. На эпюре

M X надо показать квадратную параболу выпуклостью вниз, которая имеет экстремум. Используя наиболее удобный вариант из рассмотренных в при-

мере №6, получаем расстояние от сечения 4–4 до экстремума:

QY ,4− 4 = 3ql =1,5l. 2q 2q

Аналогично можно найти расстояние от сечения 3–3 до сечения с экстремальным моментом:

QY ,3−3 = 9ql = 4,5l. 2q 2q

Для проверки убедимся, что суммарная величина найденных отрезков

равна длине участка 3–4. Величину экстремального момента можно вычислить, подставив в функцию MX (z) на участке 3–4 z = 4,5l + 3l = 7,5l :

M X ,ЭКСТ = −q (7,5l)2 + 15ql (7,5l − 3l) = 11,25ql2 .

Можно найти экстремальный момент и не пользуясь функцией MX (z),

а рассмотрев равновесие соответствующей отсеченной части (рис. 44в):

M X ,ЭКСТ = 15ql 4,5l − 2q 7,5l 7,52 l = 11,25ql .

Откладываем экстремальный момент (плюс – вниз!) и проводим через три точки квадратную параболу (рис. 43в), заштриховываем эпюру.

На последнем участке балки 5–6 удобнее строить эпюры, рассматривая при определении в.с.ф. левую отсеченную часть. Имея достаточный навык,

можно сразу сказать, что на левом конце балки QY ,6− 6 = 4ql и M X ,6− 6 = 1ql2 . Если это не очевидно, то надо рассмотреть отсеченную часть балки, представленную на рис. 45г:

Y =QY ,6−6 − 4ql = 0, QY ,6−6 = 4ql;

momX = M X ,6− 6 − ql2 = 0, M X ,6− 6 = ql2 .

На основании дифференциальных зависимостей устанавливаем вид эпюр на участке 5–6:

qY (z) ≡ 0 = Qy′(z) QY (z) = M X ′(z) = const M X (z) − линейная.

Теперь, отложив на эпюрах найденные ординаты в сечении 6–6, проводим на эпюре QY горизонтальную прямую (т.е. постоянную), а на эпюре M X

соединяем ординаты наклонной прямой (M X ,5− 5 = M X ,4− 4 ) . Заканчиваем решение задачи, поставив знак на эпюре QY и сделав штриховку.

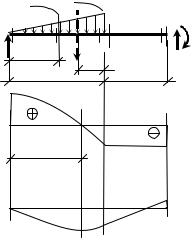
Пример 8. Для балки, показанной на рис.43а, построить эпюры внут-

ренних силовых факторов.

Заданы: l

– параметр длины участков балки,

– параметр нагрузки.

Решение.

Особенность этого примера в том, что задана неравномерно распреде-

ленная нагрузка.

Опорные реакции в начале решения не определяем, так как опора одна.

На эпюрах для этой балки получается два участка и, соответственно, четыре

характерных сечения (рис. 45а).

На левом конце балки (сечение 1–1)

а)

qy(z)

величины внутренних усилий очевидны:

3ql 2

QY ,1−1 = 4ql,

M X ,1−1 = 0 .

4ql

z 3

2 3

3,5ql

Определим в.с.ф. в

сечении

2–2

5l/3

5ql

(рис. 46а):

б) 4

= 4ql − 1 5l 3q = −3,5ql,

ЭпQy

Y ,1−1

z0=3,65l

(ql)

− 1

5l 3q 5l

= 15 ql2.

3,5

M X ,1−1 = 4ql 5l

в)

ЭпMx

Вычисляя

M X ,

учитываем,

что

(ql 2)

7,5

равнодействующая

распределенной

на-

9,74

грузки проходит через центр тяжести фи-

Рис. 45. Эпюры в.с.ф. в однопролетной

гуры, изображающей интенсивность рас-

балке с нагрузкой, распределенной ли-

пределенной нагрузки. В данном случае

нейно-переменно по длине

это 2

5l от левого конца балки или

1 5l

от правого конца участка. Полученные ординаты откладываем на эпюрах

(рис. 45б и 45в).

Используя дифференциальные зависимости, устанавливаем вид функ-

ций Qy (z)

и MX (z) на участке 1–2:

qY (z) − линейная QY (z) − кв. парабола M X (z) − кубическая парабола.

На эпюре QY

квадратную параболу надо провести выпуклостью вверх,

′

= −qY ,1−1 = 0 . Следовательно,

касательная к пара-

так как производная QY ,1−1

боле в сечении 1–1 горизонтальна.

На эпюре MX (z) надо показать кубическую параболу выпуклостью

вниз (по «правилу паруса»). Но чтобы провести ее, необходимо вычислить

величину экстремального момента на этом участке. Положение сечения с

экстремальным моментом в данном случае можно найти лишь одним спосо-

бом,

используя аналитическое выражение Qy (z) . Рассмотрим отсеченную

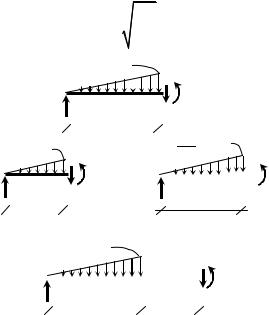
часть балки, представленную на рис.46б. Необходимо найти функцию qy (z) . Для этого используем подобие треугольников (рис.45а):

qY (z)

qY (z) =

3q .

Теперь из условия равновесия отсеченной части (рис.46б) получаем:

Q (z) = 4ql −

z q

(z)

= 4ql −

(

3q)

= 4ql −

3 z2

q .

10l

Для определения z0 имеем квадратное уравнение

(z ) = 4ql − 3 z02

q = 0

z 2

= 40 l2

= l

40 = 3,65l .

10l

а)

Величину

экстремального

2-2

изгибающего момента можно вы-

Mx,2-2

числить,

записав функцию MX (z)

4ql

Qy,2-2

(рис. 46б) или рассмотрев отсе-

qy(z)

ченную

часть для

сечения

5–5

б)

в)

Mx,ЭКС

(рис. 46в):

4ql

Mx(z)

4ql

M X ,ЭКСТ = 4ql 3,65l −

3,65l ×

Q y(z)

Z0=3,65l

×(3,65l 3q) 3,65l

= 9,74ql2.

г)

4-4

Mx,4-4

Показываем

вычисленный

4ql

Qy,4-4

M X ,ЭКСТ , проводим

кубическую

параболу, ставим знак на эпюре

Рис. 46. К определению усилий в бал-

и штрихуем эпюры.

сечении

3–3

внутренние

ке с треугольной нагрузкой

усилия такие же, как и в сечении 2–2, так как расстояние между ними равно нулю и никаких внешних сил между ними не приложено. Научастке3–4

q (z) ≡ 0 = Q		′ (z) Q (z) =	M	′ (z) = const
Y	y	Y		X
M X (z)	− линейная.
На эпюре		QY проводим	горизонтальную прямую, ставим знак и

штрихуем. Для завершения решения осталось найти M X в сечении 4–4. Рас-

смотрим соответствующую отсеченную часть (рис. 46г):

M X ,4−4 = 4ql 8l − 12 5l 3q (3l + 53l ) = −3ql2.

Откладываем M X ,4− 4 на эпюре (минус – вверх!), соединяем прямой

линией с предыдущей ординатой и штрихуем эпюру (рис. 45в).

Покажем на рис. 45а опорные реакции, которые равны усилиям в сече-

нии 4–4.

6. ПРОВЕРКИ ЭПЮР ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ

Овладеть методом сечений для определения внутренних силовых факторов очень важно, но еще важней уметь проверить правильность решения. Все проверки эпюр в.с.ф. основаны на условиях равновесия и дифференциальных зависимостях. Рекомендуется выполнять проверки в следующем порядке:

1)Характер линий (постоянная, линейная, кривая, направление выпуклости).

2)Скачки. На эпюре продольных сил скачок там, где приложена сосредоточенная продольная сила. Величина скачка равна этой силе. Аналогично на эпюре поперечных сил, где приложена сосредоточенная поперечная сила. На эпюре моментов скачок там, где приложен сосредоточенный момент

иравен этому моменту.

3)Переломы. Перелом – это изменение скач-

ком угла наклона касательной. На эпюре изгибающих	(1) (4)
моментов перелом должен быть там, где есть скачок	(2)
на эпюре поперечных сил, т.е. там, где приложена со-
средоточенная поперечная сила. Перелом может быть	(3)
связан с увеличением скачком или уменьшением
первой производной. При этом может иметь место
изменение знака производной или нет. Варианты пе-	Рис. 47. Варианты пере-
реломов показаны на рис. 47. Линия (1) соответству-	Рис. 47. Варианты пере-
ет увеличению по модулю производной, линия (2) –	ломов
ет увеличению по модулю производной, линия (2) –

уменьшению, линия (3) – смене знака производной. Штриховая линия (4) соответствует плавному соединению линий без перелома. Для изгибающего момента все это следует из дифференциальной зависимости

dMdzX = QY (z).

4) Проверка эпюры изгибающих моментов по площадям эпюры поперечных сил. Из приведенной выше дифференциальной зависимости, как уже отмечалось, следует

M X (z) = QY (z) dz + C ,

т.е. разность между изгибающими моментами в начале и в конце участка равна площади эпюры поперечных сил.

5) При построении эпюр в.с.ф. в рамах, которые будут рассмотрены позднее, добавляется еще проверка равновесия узлов.

Проиллюстрируем использование проверок на примере №7 (рис. 43).

1.Характер линий подробно обсуждался при решении этой задачи, поэтому повторяться не будем.

2.Анализируем скачки.

К балке приложены три сосредоточенных силы – одна активная сила

( ql ) и две реактивных (4 ql и 15 ql ). Видим, что на эпюре поперечных сил

(рис. 43б) в соответствующих сечениях имеют место скачки, равные по величине сосредоточенным силам.

Можно еще обратить внимание на то, что изменение величины поперечной силы на участке 3–4 равно 12 ql и совпадает по величине с равнодей-

ствующей распределенной поперечной нагрузки на этом участке.

На эпюре изгибающих моментов (рис. 43в) показан скачок на левом конце балки величиной 1 ql2 . Он объясняется сосредоточенным моментом

ql2 , приложенным в этом сечении.

3. Переломы. Их можно обсуждать на всех эпюрах, но особенно важно сделать это на эпюре изгибающих моментов.

На эпюре поперечных сил прямые на участках 1–2 и 3–4 должны быть параллельны (рис. 43б), так как производные от Qy (z) на обоих участках

равны 2q .

На эпюре изгибающих моментов видим два перелома (рис. 43в). На стыке сечений 2–2 и 3–3 перелом со сменой знака наклона касательной. Это соответствует скачку на эпюре Qy со сменой знака. Перелом на стыке сече-

ний 4–4 и 5–5 без смены знака производной, что соответствует скачку на эпюре Qy без смены знака. При этом следует обратить внимание на то, что

угол наклона касательной в сечении 5–5 больше, чем в сечении 4–4, согласно величинам поперечных сил. Если это не выполняется, то надо проверять величины моментов или соблюдение масштаба.

На участке 1–2 правильность эпюры M X (рис. 43в) проверяем по касательной в сечении 1–1. Она должна быть горизонтальной, так как Qy,1−1 = 0 .

Если при этом ошибочно момент 9 ql2 был бы отложен вниз, то нарушилось

бы «правило паруса».
4. Проверка эпюры M X	по площадям эпюры Qy . На каждом участке
сравниваем изменение величины M X с площадью эпюры поперечных сил
(рис. 43б, 43в).		9 ql2 ;
Участок 1–2: изменение	момента	9 ql2 ;	площадь эпюры Qy равна
1 3l 6ql =9 ql2 .
2			11,25 ql2 -(- 9) ql2 =20,25 ql2 ;
Участок 3–7: изменение	момента	равно	11,25 ql2 -(- 9) ql2 =20,25 ql2 ;
площадь эпюры Qy равна 1 4,5l 9ql =20,25 ql2 .
2		11,25 ql2 - 9 ql2 =2,25 ql2 ; площадь
Участок 4–7: изменение	момента	11,25 ql2 - 9 ql2 =2,25 ql2 ; площадь

эпюры Qy	1	1,5l 3ql =2,25 ql2 .
	2

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.11.201839.37 Кб8эмп.docx
#
01.05.202515.07 Mб0Энергетик 22.04..doc
#
22.08.2019481.79 Кб51Энергоснабжение.doc
#
16.03.20161.03 Mб159эос лекции.doc
#
26.09.201934.6 Кб6ЭП.лекции.docx
#
09.05.20151.38 Mб36Эпюры ВСФ.pdf
#
08.05.2015522.24 Кб19ЭсПП 503,4.doc
#
08.05.2015584.19 Кб15ЭсПП приложения 503,4.DOC
#
16.03.201618.45 Кб39Эссе.docx
#
09.05.2015456.44 Кб33ЭССЭС КП 2013.pdf
#
09.05.20151.13 Mб19ЭССЭС ЛР 2013.pdf