
Пример расчета
Рассмотрим расчет одного из вариантов схем, представленном на рисунке _. Исходные данные представлены в таблице _.

1. Метод уравнений Кирхгофа
1.1 Принимаем условно-положительные направления токов в ветвях.
1.2 По первому
закону Кирхгофа составляем
 независимых уравнений, где
независимых уравнений, где
 — число
узлов.
— число
узлов.
Узел 1=4:
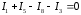
Узел 2:

1.3 По второму
закону Кирхгофа составляем
 независимых уравнений, где
независимых уравнений, где
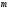 —
число контуров.
—
число контуров.
Контур I:

Контур II:

Контур III:

Контур IV:

В результате подстановки параметров схемы в уравнения, получаем систему:


Решая систему из шести уравнений с шестью неизвестными, находим токи в ветвях.

2. Метод узловых потенциалов
2.1 Принимаем условно-положительные направления токов в ветвях.
2.2 Принимаем
потенциал точки 0
 .
.
2.3 Определяем потенциалы остальных узлов, для этого составим систему уравнений по методу узловых потенциалов для двух независимых узлов.

где
 — потенциалы узлов;
— потенциалы узлов;
 — собственная
проводимость n-го
узла, равна сумме проводимостей ветвей
сходящихся в узле n;
— собственная
проводимость n-го
узла, равна сумме проводимостей ветвей
сходящихся в узле n;
 — общая проводимость
n-го и m-го
узла, равна сумме проводимостей ветвей
непосредственно соединяющих узлы n
и m;
— общая проводимость
n-го и m-го
узла, равна сумме проводимостей ветвей
непосредственно соединяющих узлы n
и m;
 — узловой ток n-го
узла
— узловой ток n-го
узла
 определяется как алгебраическая сумма
произведений ЭДС источников на
соответствующую проводимость тех
ветвей, которые примыкают к рассматриваемому
узлу.
определяется как алгебраическая сумма
произведений ЭДС источников на
соответствующую проводимость тех
ветвей, которые примыкают к рассматриваемому
узлу.
Собственные проводимости узлов.

Общая проводимость узлов.
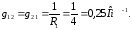
Узловые токи.

Полученные значения подставим в систему уравнений.

Решая совместно систему двух уравнений, получим потенциалы узлов.

По закону Ома для участка цепи определяем токи в ветвях.

3. Баланс мощностей
Мощность источников ЭДС:

Мощность, выделяемая в сопротивлениях схемы:

Для рассматриваемого примера баланс мощностей выполняется с достаточной точностью, следовательно, токи определены верно.
4. Потенциальная диаграмма
Для построения
потенциальной диаграммы определяем
потенциалы точек внешнего контура
относительно точки
 ,
потенциал которой принимаем равной 0:
,
потенциал которой принимаем равной 0:


