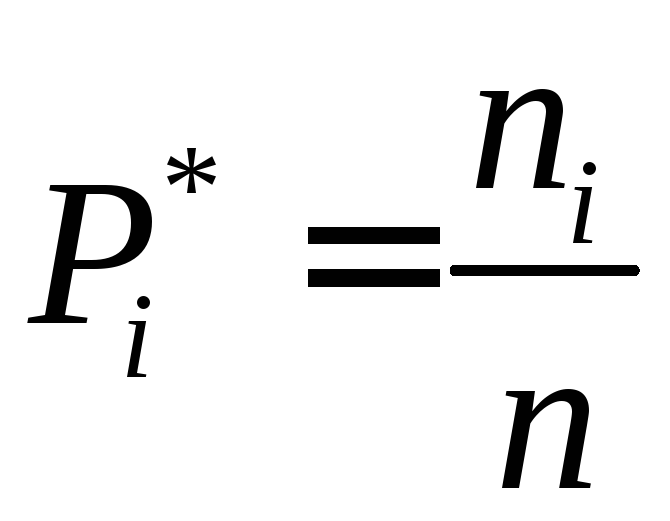4. Проверка гипотезы о нормальном распределении случайной величины.

Ввиду ограниченного числа наблюдений статистический закон распределения обычно в какой-то мере отличается от теоретического. Возникает необходимость определить: является ли расхождение между статистическим и теоретическим законами распределения следствием ограниченного числа наблюдений или оно является существенным и связано с тем, что действительное распределение случайной величины не соответствует выдвинутой гипотезе.

Для проверки гипотезы о нормальном распределении рассматриваемой величины заполним таблицу 2. Для этого:

1. Производим новую классификацию выборки: добавляем новые интервалы ик уже имеющимся и объединяем интервалы, для которыхв один.

После объединения количество интервалов .

2. Вычисляем теоретические вероятности попадания варианты в каждом интервале по формуле

,

где ,функция Лапласа

.

3. Вычисляем частоты интервалов и относительные частоты с учетом объединения интервалов.

, , , ,

,

4. Для проверки гипотезы о нормальном распределении случайной величины в качестве меры расхождения между теоретическим и статистическим распределениями выберем случайную величину (хи-квадрат)

.

Заполнив таблицу 2, вычислим значение критерия (хи-квадрат статистическое).

Случайная величина распределена по законус параметром, называемым числом степенной свободы.

Число параметров нормального распределения

Число степенной свободы .

Расхождение между статистическим и теоретическим распределениями является не существенным, если величина не превышает критического значения .

При уровне значимости и числу степенной свободынаходим критическое значение

.

Так как

,

то выдвинутую гипотезу о том, что случайная величина распределена по нормальному закону, можно с надежностью

считать правдоподобной, не противоречащей опытным данным.

Табл. 2

№	Границы классов
1
2
3
4
	Σ	1

Построим график теоретической плотности распределения

.

Для этого возьмем точек с абсциссамииз таблицы 1 и вычислим ординаты этих точек. Результат запишем в таблицу 3.

Табл. 3

N

Для более точного построения графика вычислим точку максимума

,

и точки перегиба

,

.

Сравним теоретическую и эмпирическую плотности распределения случайной величины:

Табл. 4.

N

Сравнивая значения ординат плотности распределения случайной величины и плотности относительных частот, мы наблюдаем незначительное отклонение этих величин друг от друга, что также свидетельствует о правильности выбора закона распределения.

5. Вычисление доверительных интервалов для математического ожидания и дисперсии

1. Так как гипотеза о нормальном распределении случайной величины не противоречит опытным данным, то будем считать (с некоторым риском), что случайная величина распределена нормально, причемматематическое ожидание исреднее квадратическое отклонение этого распределения неизвестны.

Доверительный интервал для оценки математического ожидания имеет вид:

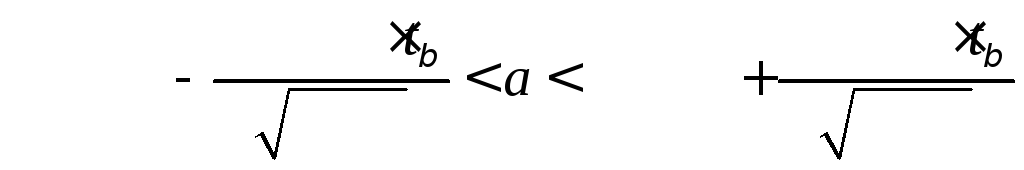
По доверительной вероятности и числу степенной свободы

находим (например, В.Е.Гмурман “Руководство к решению задач по теории вероятностей и математической статистике” приложение3)величину

,

а затем точность оценки

.

Итак, получим искомый доверительный интервал, покрывающий неизвестное математическое ожидание с заданной надежностью , т.е. интервал

2. Доверительный интервал для имеет вид:

,

Для ипо таблице (см. в учебниках В.И. Ермаков “Сборник задач по высшей математике для экономистов” приложение 3 стр. 520 или приложение 4 В.Е. Гмурман “Руководство к решению задач по теории вероятностей и математической статистике”) находим

Отсюда

Поясним смысл, который имеет заданная надежность . Из 100 выборок 95 определяют такие доверительные интервалы, в которых параметр (и) действительно заключен, и только в пяти выборках он может выйти за границы доверительного интервала.

6. Задача

Решение

16