
- •Рабочая тетрадь по математической статистике
- •Перед началом выполнения семестрового задания по математической статистике студент должен ответить на следующие вопросы:
- •Построение статистического распределения выборки.
- •Вычисление оценок математического ожидания и дисперсии
- •Построение гистограммы относительных частот
- •Проверка гипотезы о нормальном распределении случайной величины.
Рабочая тетрадь по математической статистике
Вариант _________ Группа __________
Фамилия _____________________________
Перед началом выполнения семестрового задания по математической статистике студент должен ответить на следующие вопросы:
Дискретные случайные величины. Закон распределения вероятностей дискретной случайной величины. Числовые характеристики дискретной случайной величины.
Непрерывные случайные величины. Функция распределения, плотность распределения, их взаимосвязь и свойства. Нормальный закон распределения непрерывных случайных величин, правило «трех сигм». Числовые характеристики непрерывных случайных величин.
Генеральная совокупность и выборка. Вариационный ряд. Гистограмма, эмпирическая функция распределения выборки.
Статистическое оценивание параметра распределения по выборке. Точечные оценки и их характеристики: несмещенность, эффективность, состоятельность.
Интервальные оценки. Доверительные интервалы. Интервальное оценивание параметров нормального распределения.
Статистические гипотезы, их виды. Понятие о проверке статистических гипотез. Ошибки 1 – го и 2 – го рода. Мощность критерия. Доверительные области. Критерий согласия Пирсона.
План выполнения семестрового задания:
Построить статистическое распределение выборки.
Вычислить оценки математического ожидания и дисперсии.
Построить гистограмму относительных частот, установить статистический (эмпирический) закон распределения и записать его функцию плотности. С помощью критерия
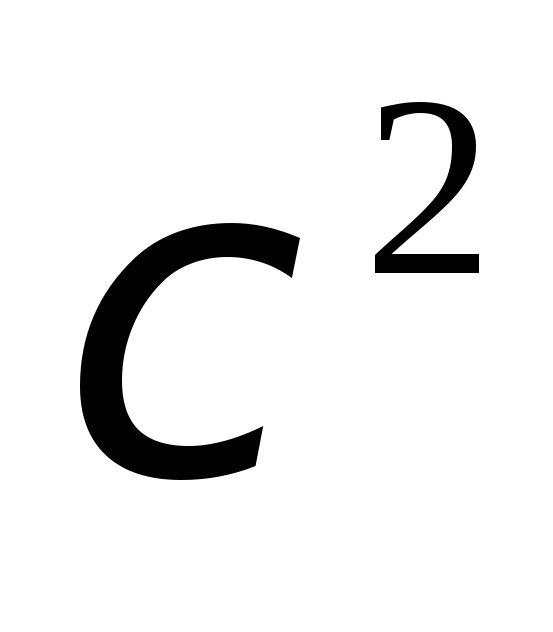 (Пирсона)
проверить гипотезу о согласии
эмпирического закона распределения
случайной величины
(Пирсона)
проверить гипотезу о согласии
эмпирического закона распределения
случайной величины с нормальным законом распределения
(законом Гаусса).
с нормальным законом распределения
(законом Гаусса).Построить кривую нормального распределения, приняв за параметры кривой найденные оценки математического ожидания и дисперсии (желательно на одном чертеже с гистограммой).
Вычислить доверительный интервал для математического ожидания и дисперсии.
Решить указанную задачу.
Построение статистического распределения выборки.
Данную выборку преобразуем в вариационный (интервальный) ряд. Для этого:
Упорядочим выборку, т.е. запишем все значения
 случайной величины
случайной величины
 в возрастающем порядке
в возрастающем порядке
Объем выборки составляет

минимальное
значение
![]()
максимальное
значение
![]()
Разобьем диапазон изменения случайной величины
 на интервалы. Число интервалов
определяется по следующей полуэмпирической
формуле
на интервалы. Число интервалов
определяется по следующей полуэмпирической
формуле
![]()
с округлением до ближайшего целого.
![]()
Ширину каждого интервала берем одинаковой и равной
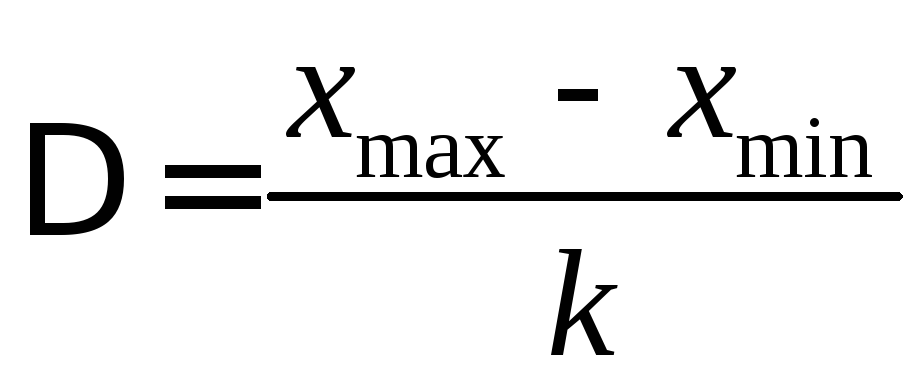 .
.
Величину
![]() выбираем с точностью выборки и округляем
в сторону завышения.
выбираем с точностью выборки и округляем
в сторону завышения.
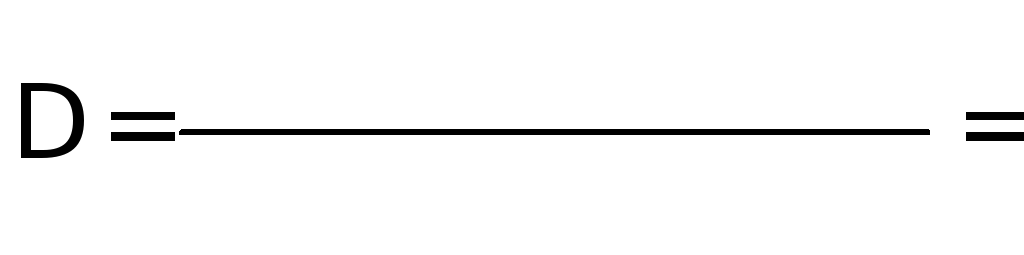 ,
,
![]() .
.
Границы интервалов вычисляем по формуле
![]() ,
,
![]() .
.
![]()
![]()
![]()
=
=
По протоколу выборки подсчитываем частоту интервала - количество элементов
 ,
попавших в
,
попавших в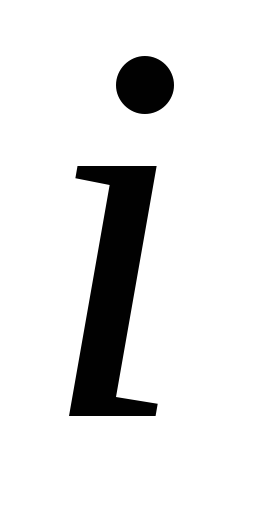 -тый
интервал. Если элемент совпадает с
границей интервала, то он относится к
предыдущему интервалу.
-тый
интервал. Если элемент совпадает с
границей интервала, то он относится к
предыдущему интервалу.
![]()
![]()
![]()
=
Вычисляем относительные частоты интервалов
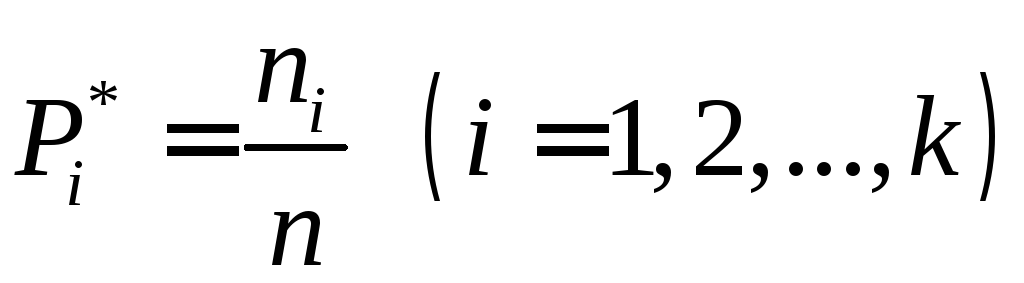 .
.
![]()
![]()
![]()
=
Полученные данные вносим в первые четыре столбца таблицы 1.
