1.3. Методические указания к выполнению курсовой работы

Выполнение курсовой работы следует начинать с изучения системы радиосвязи указанной в задании. С этой целью следует уяснить назначение системы радиосвязи, состав и принцип ее построения, основные технические характеристики, возможности и предоставляемые услуги. Необходимо самостоятельно изучить основные характеристики применяемых сигналов: методы модуляции, способы помехозащищенного кодирования, стандарты и протоколы связи, метод кодирования-декодирования речевых сигналов, организацию каналов управления системы радиосвязи и т.д. Описание стандарта не должно превышать одной трети объема пояснительной записки, так как основное внимание следует уделить усвоению теоретического материала и его применению для обработки сигналов.

1.4. Теоретические основы моделей линейного предсказания

1.4.1. Модель авторегрессии в корреляционной теории

1.4.1.1. Принципы построения модели авторегрессии

В основу модели АР положена корреляция отсчета случайного процесса в текущий момент времени с некоторым конечным или бесконечным числом отсчетов в предыдущие моменты времени. Корреляционные связи позволяют осуществить регрессию текущего отсчета на предшествующие. Такой вид регрессии называется авторегрессией. В уравнении АР текущий отсчет представляется взвешенной суммой предыдущих с некоторыми коэффициентами веса

, (1)

где - коэффициенты АР, - некоррелированные случайные отсчеты, - порядок модели АР.

Величина

, (2)

называется предсказанием случайной величины. Разность между текущим значением отсчета и его предсказанием называется ошибкой предсказания

. (3)

Величина характеризует, по существу, максимальную точность предсказания текущего отсчета, а ее статистические свойства определяют выбор порядка модели АР.

Из (1) видно, что построение АР модели случайного процесса сводится к нахождению коэффициентов АР и определению порядка . Умножив правую и левую части (1) на и усреднив, можно получить систему уравнений

, , (4a)

, (4б)

где - значения функции корреляции случайного процесса

- дисперсия ошибок предсказания модели АР, - дисперсия случайного процесса . Набор уравнений (4а) и (4б) называется полной системой уравнений Юла - Уокера. Решением этой системы являются коэффициенты АР и дисперсия ошибок предсказания. При выводе уравнений (4а) было учтено, что

, , , (5a)

, , . (5б)

Соотношения (5) следуют из некоррелированности ошибок предсказания . Решение системы уравнений (4а) можно представить в матричном виде

, (6a)

где

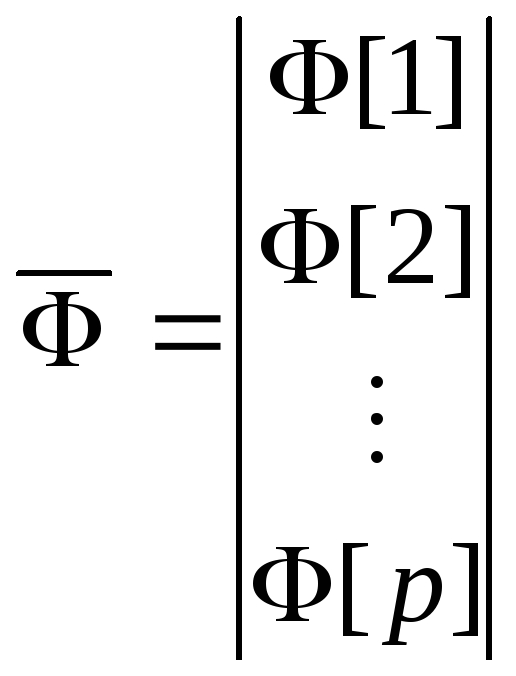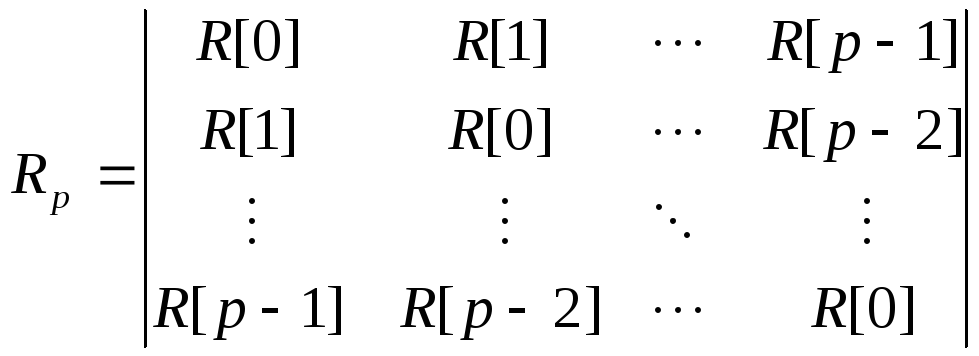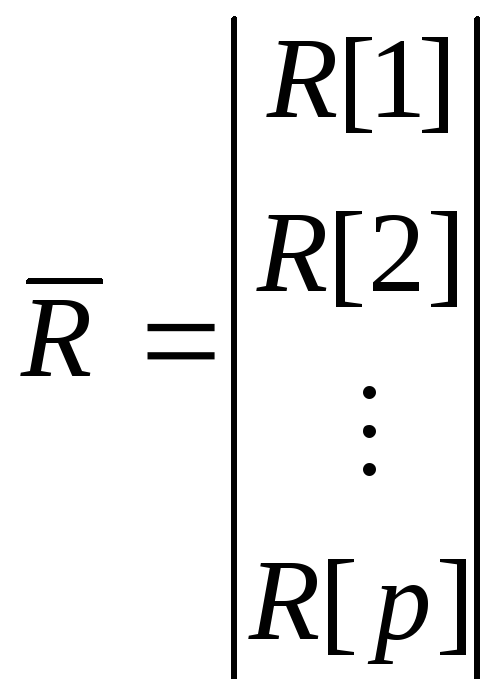,,. (6б)

Как видно из (4а), уравнение не изменится если вместо использовать нормированные значения функции корреляции , которые будем называть коэффициентами корреляции. Очевидно, что при этом параметры модели АР останутся прежними.

Как следует из (6а,б), для первого порядка модели АР

. (7)

Для модели АР второго порядка коэффициенты АР равны

,

. (8)

Отметим важное свойство коэффициентов АР, которое не сохраняется, как будет показано в следующей главе, для ОАР модели. Коэффициенты АР минимизируют дисперсию ошибки предсказания

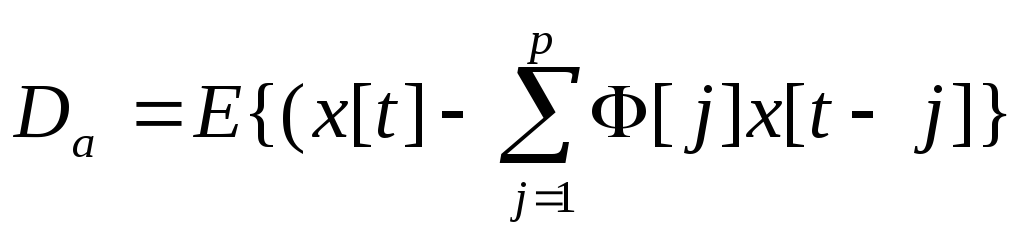. (9)

В этом легко убедиться, продифференцировав (9) по и приравняв производную к нулю. При этом полученная система уравнений совпадает с (4а).

Достоинством модели АР является ее конструктивность, заключающаяся в возможности синтеза довольно простым образом алгоритмов обработки случайных процессов. На рис. 1 представлен АР фильтр предсказания (обеляющий фильтр), алгоритм действия которого описывается выражением (3). Он состоит из линий задержки, усилителей с коэффициентами усиления ,и сумматора. Ошибки предсказания на выходе этого будут отчетами белого шума, а точнее некоррелированным процессом. Дисперсия ошибки предсказания на выходе фильтра будет иметь минимальное значение, если коэффициенты АР найдены из уравнения (4а).

Порядок процесса АР определяется с использованием различных критериев, как правило, основанным на минимизации некоторой теоретико-информационной функции. Для определения порядка модели пользуются методами Бартлетта [ ], Акайке, Парзена. Порядок модели можно находить из условия не убывания дисперсии ошибки предсказания при дальнейшем повышении порядка. Довольно эффективным методом определения порядка модели АР является метод, основанный на проверке близости корреляционной функции случайного процесса на выходе обеляющего АР фильтра к корреляционной функции белого шума.

Процессы АР можно характеризовать конечным числом значений функции, определяемой корреляционной функцией. Такая функция носит название частной автокорреляционной функции. Ее можно выразить через коэффициенты АР, порядок которых изменяется от единицы до . Т.к. коэффициент АР с номером полагается равным нулю, то процесс АР можно характеризовать конечным набором не равных нулю коэффициентов АР с номером равным р для моделей АР с порядками от единицы до -, . Поэтому значения частной автокорреляционной функции полагаются равными , . Можно показать, что первые три значения частной автокорреляционной функции описываются выражениями вида

,

,

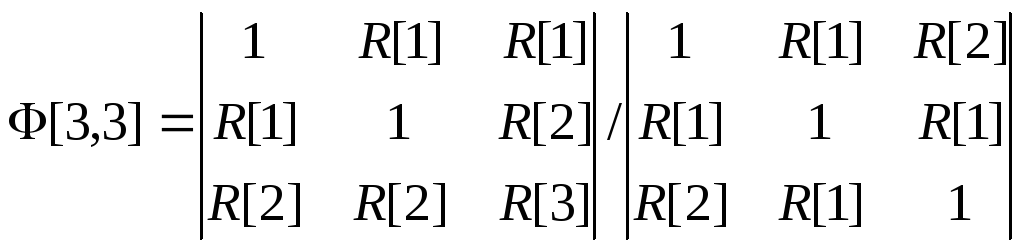. (2.10)

Достоинством частной автокорреляционной функции по сравнению с автокорреляционной функцией является ее конечная длина. Как показал Бартлетт [], значение частной автокорреляционной функции можно полагать равным нулю, если оно меньше , где - длина реализации, по которой производилась оценка значений функции корреляции. Таким образом, по существу производится оценка порядка модели АР.

2. Спектр процесса авторегрессии

Формула для нахождения спектра модели АР лежит в основе параметрического спектрального оценивания. Для ее вывода будем рассматривать процесс АР как реакцию фильтра , на вход которого подаются некоррелированные отсчеты . Используя -преобразование, можно показать что -преобразование передаточной функции АР фильтра имеет вид

, (2.11)

где

, . (2.12)

-преобразования автокорреляционных функций выходного и входного процессов связаны соотношением

. (2.13)

Чтобы найти СПМ выходного АР процесса необходимо в (2.13) сделать замену и положить, что для белого шума постоянная величина. Тогда из (2.13) следует

. (2.14)

Выражение (2.14) широко используется в параметрическом методе спектрального оценивания. В качестве параметров, полностью характеризующих спектральную оценку случайного процесса, выступают коэффициенты АР и порядок модели. Параметрическое спектральное оценивание обладает рядом достоинств по сравнению с традиционными методами спектрального оценивания. К ним относятся: более высокое спектральное разрешение при использовании коротких выборок, отсутствие боковых лепестков.

С помощью модели АР можно получать спектральные оценки процессов со сложной формой СПМ. Для этого может быть придется использовать модели АР бесконечного порядка. На основе модели АР легко синтезируются оптимальные фильтры подавления, согласованные не только по частоте и полосе спектра, но и по форме спектра случайного процесса. Достоинством формулы (2.14) является возможность анализировать СПМ в аналитическом виде, что невозможно сделать при использовании традиционных методов спектрального оценивания на основе преобразования Фурье. Например, можно найти формулы для определения частоты максимумов и минимумов СПМ.

Чтобы определить положение максимума или минимума АР оценки СПМ, нужно взять производную от (2.14) по и приравнять ее к нулю. Корни полученного уравнения определяют положение экстремумов функции СПМ. При можно показать, что

, (2.15)

где - частота на которой находится максимум СПМ.

1.4.1.3. Характеристическое уравнение модели авторегрессии

Модель АР, описываемая уравнением (2.1), может быть представлена в операторной форме

, (2.16)

где оператор АР имеет вид

. (2.17)

Действие оператора сдвига z на текущий отсчет описывается следующим образом

. (2.18)

Из условия устойчивости формирующего АР фильтра с рациональной передаточной функцией (2.11) следует условие стационарности АР процесса. Для проверки стационарности случайного АР процесса используется характеристическое уравнение

. (2.19)

Если корни характеристического уравнения (2,19) лежат внутри единичного круга на комплексной плоскости, то процесс АР удовлетворяет условию стационарности. Характеристическое уравнение (2.19) можно представить в виде

. (2.20)

Условие стационарности заключается в том, что корни характеристического уравнения (2.20) должны лежать вне единичного круга на комплексной плоскости.

Используя (2.19) и (2.20) оператор АР (2.17) можно представить в виде

. (2.21)

Из (2.21) следует, что уравнение АР (2.1) можно записать следующим образом

. (2.22)

Сравнивая (2.1) и (2.22) найдем связь между коэффициентами АР и корнями . Приведем соответствующие формулы для

, (2.23a)

;

, (2.23б)

;

;

, (2.23в)

;

;

;

, (2.23г)

где первый индекс в квадратных скобках указывает на соответствующий порядок модели. Полученные формулы оказываются весьма полезными для определения коэффициентов АР по заданным характеристикам случайного процесса.

Отметим, что корни характеристического уравнения полностью описывают модель АР. Свойства модели зависят параметров, через которые они выражаются. Если корень действительный, то его можно представить в виде экспоненциальной функции

, (2.24а)

где - коэффициент демпфирования равный , где -ширина полосы -го пика СПМ. Тогда действительные корни характеристического уравнения принимают вид

. (2.24б)

Комплексные корни характеристического уравнения описываются выражениями

, , (2.25)

где - собственная частота модели АР с поправкой на демпфирование, соответствующая -тому пику СПМ.

4. Генерация коррелированного случайного процесса

В задачах статистического моделирования часто возникает необходимость генерации случайного процесса с заданной корреляционной функцией или с заданной формой и характеристиками СПМ. Для этих целей эффективно использовать генератор процесса АР показанный на рис. 2. Генерация случайного процесса осуществляется методом порождающего случайного процесса. Порождающий процесс в виде белого шума, обычно с гауссовой функцией распределения, пропускается через формирующий фильтр параметры которого определяются соответствующей моделью АР.

Для генерации процесса нужно выбрать необходимое количество пиков СПМ. Тогда порядок модели АР равен, как правило, удвоенному значению числа пиков. Так, для СПМ с одним пиком порядок модели равен 2, с двумя пиками порядок модели равен 4. Затем задаются частотой пика и его шириной полосы. Вычисленные значения корней характеристического уравнения по формулам (2.24), используются для нахождения коэффициентов АР. Для этого корни подставляются в соответствующие выражения (2.23). Генерация процесса осуществляется с помощью рекуррентного выражения (1) с использованием порождающего белого шума a[t].

Решетчатые фильтры для стационарных случайных процессов

Построение АР модели или синтез АР фильтра требуют вычисления коэффициентов АР. Для этого не­обходимо обращать корреляционную матрицу, а эта операция, как правило, сопряжена с большим объемом вычислений. Поиски эффективных алгоритмов вычисления коэффициентов АР привели к синтезу решетчатых структур. Решетчатые структуры могут быть реализованы в виде решетчатых фильтров (РФ). Параметрами РФ являются коэффициенты отражения и число звеньев фильтра. Коэффициенты отражения однозначно свя­заны с параметрами АР и определяются, в конечном счете, корреляционной функцией случайного процесса. Число звеньев РФ равно порядку АР модели РФ, также как и АР фильтры, являются фильтрами предсказания, минимизирующими дисперсию ошибки предсказания.

Несмотря на то, что АР фильтры и РФ математически эквивалентны, между ними существует ряд раз­личий, существенных с практической точки зрения. При цифровой реализации фильтров особое значение иг­рает шум округления. Его появление связано с тем, что значения величин приходится представлять конечным числом разрядов. Как показывает опыт, в этом отношении РФ более эффективны. Объясняется это тем, что ошибки округления i-1-го звена в РФ частично компенсируются в i-м звене РФ, чего нет в АР фильтрах. Дру­гим существенным свойством цифровых фильтров является их чувствительность к квантованной форме пред­ставления параметров фильтра. Поэтому, естественно, возникает вопрос: насколько сильно зависят характе­ристики фильтра от отклонения величин параметров. Доказано, что РФ менее чувствительны к погрешностям квантования параметров по сравнению с фильтрами прямой реализации. При синтезе РФ, состоящего из p звеньев, используются те же коэффициенты отражения, что и у p-1-звенного фильтра. В АР фильтре же при увеличении числа звеньев фильтра, приходится заново пересчитывать все коэффициенты АР фильтра. Следо­вательно, использование РФ для обработки случайных сигналов имеет ряд преимуществ перед АР фильт­рами.

2.3 Синтез решетчатого фильтра

Несмотря на близость РФ к АР фильтрам, использование РФ требует введения новых понятий и соот­ношений, на основе которых выводится структура РФ. Прежде всего, необходимо остановиться на выводе ре­куррентных соотношений, которые носят название алгоритма Левинсона-Дарбина. Алгоритм позволяет вы­числять коэффициенты отражения РФ по найденным коэффициентам АР модели сигнала 1- р порядков.

По аналогии с фильтром прямого предсказания для сигнала, описываемого моделью АР р-го порядка, можно ввести фильтр обратного предсказания, описываемый выражением

, (2.15)

где - коэффициенты фильтра обратного предсказания, состоящего из р звеньев, определяемые моде­лью АР , введенной во второй главе, - ошибка обратного предсказания на выходе р-го звена фильтра. Уравнение описывает регрессию значения случайного процесса х_t-p-1 на последующие х_t-p, х_t-1-p, ...,х_t-1 . Значения коэффициентов фильтра обратного предсказания находятся с помощью системы урав­нений, аналогичной системе уравнений Юла-Уокера . Объединяя уравнения (2.4а) и (2.4б) , можно представить обобщенные уравнения Юла-Уокера в матричном виде

, (2.16)

где -квадрат СКО, равный дисперсии ошибки прямого предсказания, R_p - корреляционная матрица (p+1) порядка

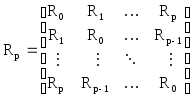. (2.17)

Чтобы не выходить за рамки общепринятых в теории решетчатых фильтров обозначений (например [16, 17]), в дальнейшем изложении будет использоваться замена и .

Умножив левую и правую части уравнения на; j=1, p+1 и усреднив, легко получить уравнение Юла-Уо­кера для фильтра обратного предсказания, аналогичное (2.16)

, (2.18)

где - дисперсия ошибки обратного предсказания на выходе p-го звена фильтра обратного предсказа­ния.

Объединив матричные уравнения (2.16) и (2.18) можно записать более общее уравнение

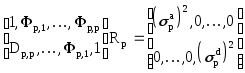. (2.19)

Очевидно, что для (р+1)- звенного фильтра должно так же выполняться соотношение типа

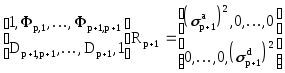. (2.20)

Но, как показано в [5, 7], от матричного уравнения (2.19) можно перейти к матричному уравнению (2.20) лишь в том случае, если коэффициенты фильтров прямого и обратного предсказания p-го порядка связаны с коэффи­циентами фильтра (p+1)-го порядка следующим образом

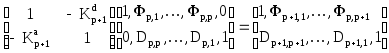, (2.21)

где- некоторые, так называемые, коэффициенты отражения. Умножив справа левую и правую часть матричного уравнения (2.21) на корреляционную матрицу R_p+1 , можно показать, что коэффициенты отражения удовлетворяют соотношениям

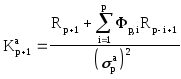, (2.22а)

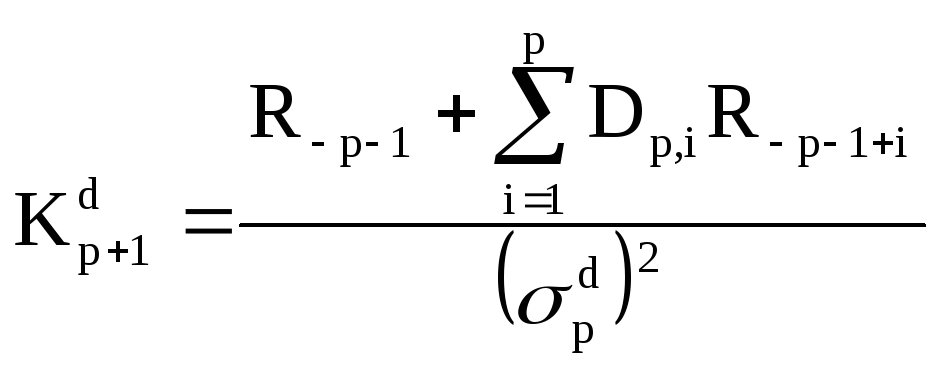. (2.22б)

Величины, входящие в соотношения (2.22а) и (2.22б), описываемые выражениями

, (2.23а)

, (2.23б)

как будет показано ниже, интерпретируются как взаимная корреляция ошибок прямого и обратного предска­зания при единичной задержке. Для скалярного случая справедливы равенства

. (2.24)

Используя соотношения (2.15), (2.22а), (2.22б) и учитывая (2.24), алгоритм Левинсона-Дарбина, позволяющий вычислять коэффициенты АР по коэффициентам отражения, можно предста­вить в виде

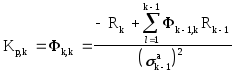, k=2, p , (2.25)

, (2.26)

, (2.27)

с инициацией

, . (2.28)

Найденный алгоритм Левинсона-Дарбина позволяет получить структуру РФ. Формулы (2.29) и (2.30) дают выражение

, (2.29)

которое с помощью (2.29) приводится к виду

. (2.30)

Аналогично можно найти выражение для ошибки обратного предсказания

. (2.31)

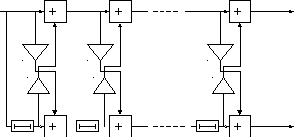
Полученные выражения (2.30) и (2.31) дают возможность представить структуру РФ в виде, изображенном на рисунке 2.1.

Рисунок 2.1 -Обеляющий РФ.

При поступлении сигнала на вход фильтра на выходе каждого звена фильтра появятся ошибки пред­сказания вперед и назад. Как видно из рисунка 2.1 ошибки предсказания вперед и назад связаны друг с другом соот­ношениями (2.30) и (2.31).

Как можно показать, используя соотношение (2.31), решение задачи минимизации дисперсии ошибки предсказания относительно коэффициента отражения К_p дает следующее выражение для коэффици­ента отражения

. (2.32)

К этому же соотношению можно придти путем несложных преобразований выражений (2.30) и (2.31). Таким обра­зом, РФ, коэффициенты отражения которого определяются алгоритмом Левинсона-Дарбина, минимизирует дисперсию ошибки предсказания. Выражение (2.32) дает удобную оценку коэффициентов отражения РФ, позволяющее обновлять их при адаптации фильтра.

Из рисунка 2.1 видно, что текущий отсчет случайного процесса можно представить в виде

, , (2.33)

т.е. взвешенным суммированием ошибок обратного предсказания в предшествующий момент времени с ко­эффициентами веса, равными коэффициентам отражения. Случайная величина х_t , представленная в виде ряда, полностью определяется коэффициентами разложения, роль которых играют коэффициенты отра­жения. Таким образом, коэффициенты отражения полностью характеризуют случайный процесс в рамках мо­дели АР. Это свойство коэффициентов отражения РФ позволяет использовать их в качестве информативного признака при распознавании.

2.4 Примеры обработки стационарных случайных процессов с помощью решетчатых фильтров

Неадаптивные РФ используются для обработки стационарных коррелированных процессов. Примерами задач, решаемых с помощью таких фильтров, может служить применение РФ для подавления или обеления стационарных коррелированных помех, измерение некоторых параметров сигнала, кодировании и генерации случайных процессов и синтез речи, создание эффективных вычислительных алгоритмов и т.д.

Эффективность обработки сигналов РФ определяется точностью АР моделирования этих сигналов, достоверностью используемых оценок параметров фильтра и сигнала, скоростью и объемом необходимых вычислений. Наиболее простым способом проверки соответствия параметров РФ характеристикам обрабатываемых сигналов может служить мера близости сигнала на выходе РФ к белому шуму. Это следует из принципа построения РФ по минимуму дисперсии ошибки предсказания.

1.2.2. Генерация случайных процессов на основе фильтра с решетчатой структурой

Дальнейшее развитие теории в области предсказания временных рядов на основе модели АР привело к созданию так называемых фильтров на решетчатых структурах. Реализация решетчатых структур в виде решетчатых фильтров (РФ) предсказания по методу наименьших квадратов выявила целый ряд достоинств РФ. Особенно это касается адаптивных методов обработки случайных процессов. В стандарте GSM осуществляется адаптивная блочная обработка речи на основе фильтров предсказания с решетчатой структурой. Блочная адаптивная обработка процессов отличается от пошаговой тем, что параметры фильтра пересчитываются не с получением каждого нового отсчета данных, а по последовательным блокам данных. Параметры речи, а также процесс на выходе адаптивного РФ сформированные кодером на передающем сотовом телефоне, покадрово передаются через базовую станцию на приемник сотового телефона корреспондента. Декодер сотового телефона по принятым данным восстанавливает речевой сигнал. Для генерации речи применяется формирователь на базе РФ с обратной связью. Структура такого генератора приведена на рис. 2.

+

+

+

+

+

+

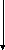
Рисунок 2.- Генератор коррелированного случайного процесса на

решетчатом фильтре с обратной связью.

РФ с прямым прохождением сигнала и РФ с обратной связью, имеющие одинаковые коэффициенты отражения, выполняют инверсные операции над входным сигналом. Если на вход РФ с прямым прохождением сигнала подается коррелированный случайный процесс, т. е. , то на выходе получаем ошибку предсказания типа белого шума . В случае же когда на вход РФ с обратной связью подается случайный процесс типа белого шума, т. е. , то на выходе формируется коррелированный случайный процесс, т. е. .

Работа генератора с кратковременным предсказанием на РФ описывается системой двух уравнений

, (7а)

, (7б)

где - коэффициенты отражения РФ; - число звеньев РФ; и - ошибки прямого и обратного предсказания в -м звене РФ в момент времени .

Применение для кодирования речи коэффициентов отражения РФ, которые являются также коэффициентами частичной корреляции случайного процесса, являются более предпочтительными, по сравнению с коэффициентами АР по следующим причинам:

• гарантируется стабильность работы генератора на РФ, т. к. согласно (8) и (10) 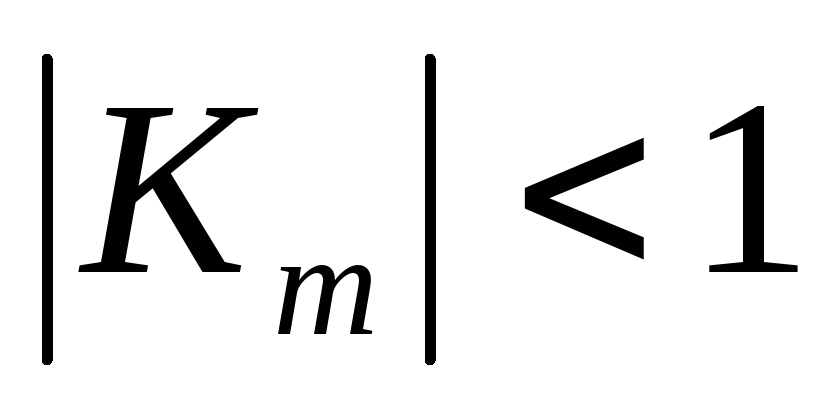, а это является необходимым условием, чтобы передаточная функция была минимально фазовой функцией и ее полюсы находились внутри единичного круга на комплексной плоскости;

• коэффициенты 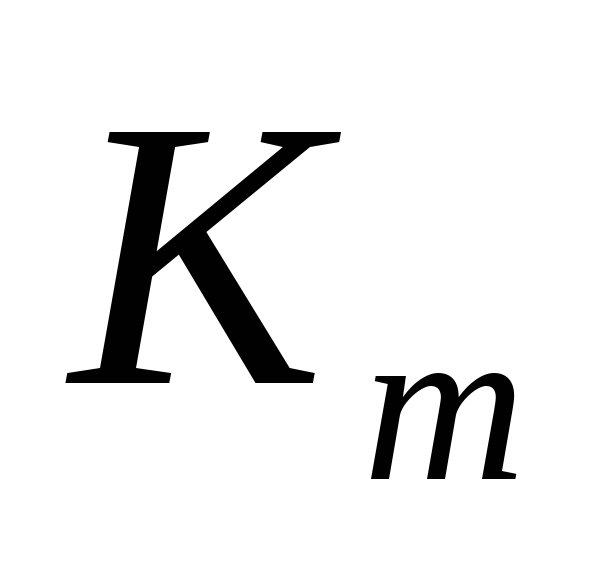нечувствительны к ошибкам квантования;

• при переходе от 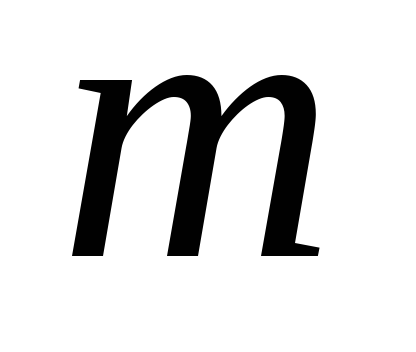-звенного к 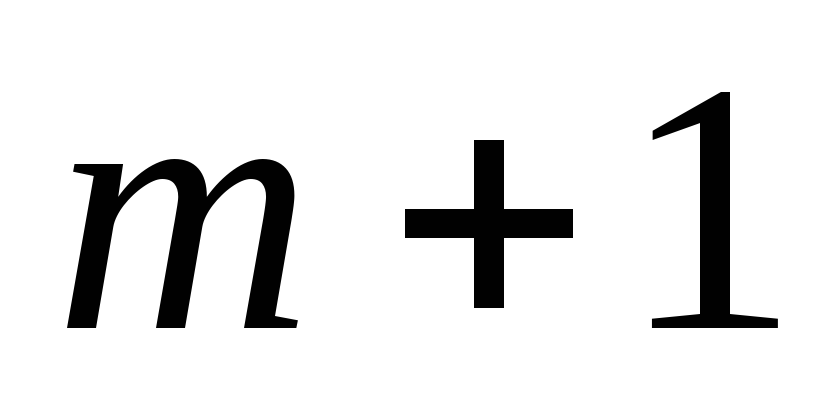-звенному фильтру, значения 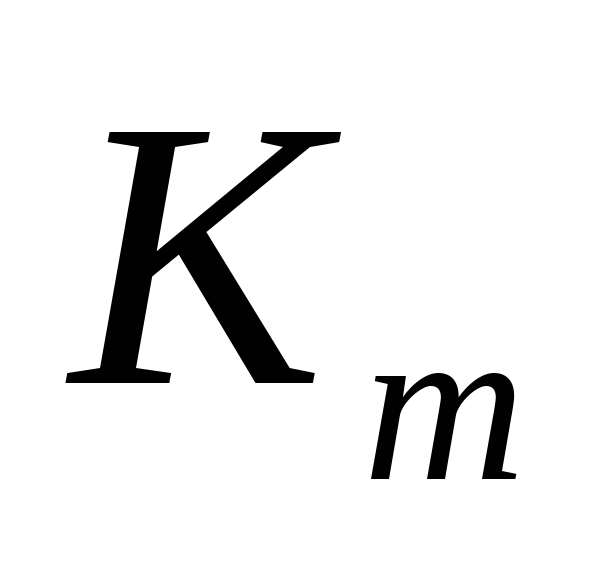не пересчитываются, в то время как коэффициенты АР нужно пересчитывать заново;

• коэффициенты отражения анализирующего и синтезирующего фильтров совпадают, что, впрочем, характерно и для коэффициентов АР.

В стандарте GSM в качестве порождающего процесса , который подается на вход синтезатора речи, используют ошибки предсказания анализирующего РФ, пропущенные через НЧ фильтр, с частотой среза 3-4 кГц. Хотя такой способ возбуждения требует существенного увеличения скорости передачи до

9.4 кбит/с, качество восстановленного в декодере сигнала речи соответствует качеству передаваемой речи в цифровых каналах связи ISDN и превосходит качество речи в аналоговых радиотелефонных системах.

Можно показать, что передаточные функции анализирующего и синтезирующего РФ также описываются выражениями ( ) и ( ) соответственно.

Высокое качество передачи речи в стандарте GSM достигается не только учетом корреляции между соседними дискретизированного речевого сигнала, но и учетом тонкой структуры речевого сигнала – корреляции между отсчетами в соседних периодах основного тона. С этой целью используются предикторы с кратковременным и долговременным предсказанием соответственно. Синтезатор речи с кратковременным предсказанием описывается системой уравнений ( ) и показан на рис. 2.

Выражение для долговременного предсказания в стандарте GSM определяется следующим образом

, (11)

где - число отсчетов в периоде основного тона.

Тогда передаточная функция анализирующего фильтра может быть представлена в виде

. (12)

Передаточная функция синтезирующего фильтра описывается выражением, аналогичным ( )

. (13)

Систему уравнений описывающую синтезирующий РФ с долговременным предсказанием можно получить из ( )

, (14)

. (15)