
ргр01
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФГАОУ ВПО «УРАЛЬСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ ИМЕНИ ПЕРВОГО
ПРЕЗИДЕНТА РОССИИ Б.Н. ЕЛЬЦИНА» ИНСТИТУТ РАДИОЭЛЕКТРОНИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ – РТФ
КАФЕДРА ТЕОРЕТИЧЕСКИХ ОСНОВ РАДИОТЕХНИКИ
Оценка работы |
___________ |
Преподаватель _________
Отчет по расчетно-графической работе
«РЕАЛИЗАЦИЯ И АНАЛИЗ ЦИФРОВОГО ФИЛЬТРА С КОНЕЧНОЙ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКОЙ»
по дисциплине «Основы цифровой обработки сигналов»
Преподаватель
Студент
Подпись |
Дата |
Ф.И.О. |
______________________________ Коберниченко В.Г.
______________________________ Вешкурцев Д.А.
Группа РИ-410501 Тема №2 Вариант 11
Екатеринбург 2015

Тема 2. Реализация и анализ цифрового фильтра с конечной импульсной характеристикой
1.Разработать алгоритм, реализующий заданный тип фильтра в частотной области (с использованием алгоритма БПФ).
2.Составить программу, позволяющую получить:
-спектр входного сигнала;
-спектральную (амплитудно-частотную) характеристику окна;
-амплитудно-частотную и импульсную характеристики фильтра;
-отклик фильтра на заданный сигнал;
-спектр выходного сигнала.
3.Проанализировать полученные результаты.
Вариант 11: |
|
|
|
|
|
|
|
|
|
|
|
|
Тип фильтра: |
|
ФНЧ |
|
|
|
|
|
|
|
|
|
|
Тип окна: |
|
Хэмминга |
|
|
|
|
|
|
|
|
|
|
Тип сигнала: |
|
Экспоненциальный радиоимпульс с |
|
|
||||||||
|
|
несущей частотой, равной fд/6 |
|
|
|
|||||||
Полоса фильтра: |
|
Δw=0.75 |
|
|
|
|
|
|
|
|
|
|
Скважность: |
|
Q=10 |
|
|
cos ( |
) |
|
|
|
|
|
|
Продискретизированный( ) = |
|
|
|
|
|
Тд |
|
|||||
Непрерывный сигнал: |
сигнал: |
д |
( |
) = |
|
Тд |
cos ( |
|
) |
|||
|
|
|
|
|
||||||||
|
|
= 2 |
= 2 |
|
6 |
|
|
|
|
|
|
|
|
|
д |
Тд = |
|
|
|
|
|
|
|||
|
|
|
6 |
|
|
3 |
|
|
|
|
|
|
|
Tд ( |
) = |
Тд |
cos ( |
|
|
|
|
|
|
|
|
Где: |
|
3 ) |
|
|
|
|
|
|
||||
|
– период дискретизации; |
|
|
|
|
|
||||||
n – номер отсчета;
α – параметр сигнала.
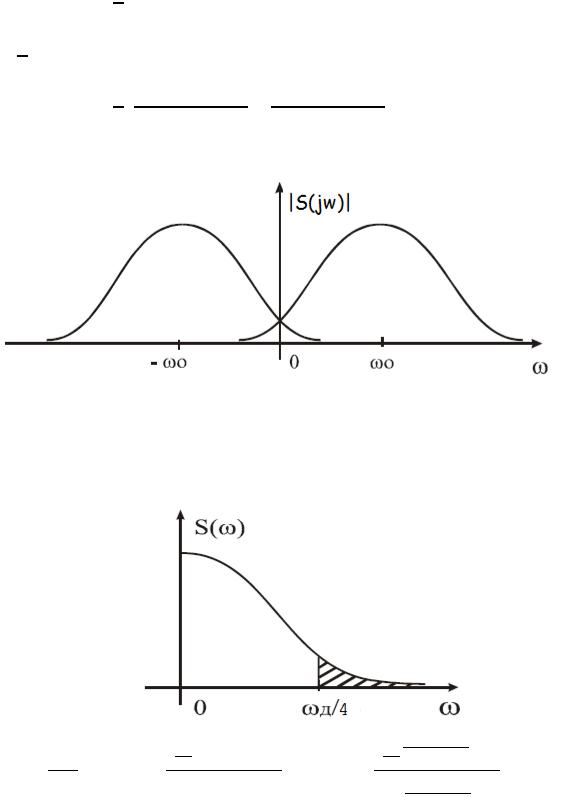
Нужно найти параметры дискретизированного сигнала: α и Тд Спектр сигнал найдем, используя преобразование Фурье:
( |
) = |
∞ |
|
∞ |
cos( |
|
) |
|
|
|
|
|
|
||||||||
|
|
|
= |
1 |
( |
) |
|
|
+ |
= |
|
1 |
∞ |
2 |
|
|
|
||||
= |
|
( |
( |
) |
+ |
∞ |
( |
( |
) |
|
|
|
|||||||||
|
2 |
|
= |
1 |
|
1 |
|
+ |
|
1 |
|
|
|
2 |
+ ( − ) |
+ ( + ) |
|||||
Спектр непрерывного сигнала:
Параметр αTд выберем из условия обеспечения уровня неопределенности -13дБ (наложение спектров).
Уровень перекрытия считается через отношение площади «хвоста» и полезной площади. Для упрощения расчетов рассмотрим на одной половинке спектра.
|
пол |
∫ |
∞ |
| ( |
)| |
|
∫ |
∞ |
+ |
|
|
д |
д |
||||||||
20lg |
пом |
= 20lg |
|
|
|
= 20lg |
1 |
|
||
д |
|
|
д |
|
||||||
|
|
| ( |
)| |
|
|
1 |
|
|||
|
|
∫ |
|
∫ |
|
+ |
||||
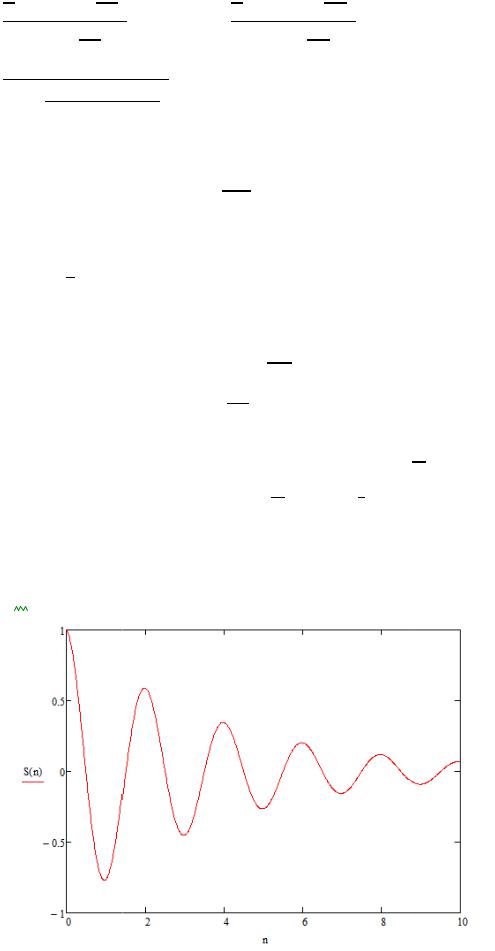
20 9 |
2 |
− ; < |
д |
д |
= − 13; |
2 |
− ; < |
д |
д |
= 20 |
, |
|
; < |
6 |
|
; < |
6 |
|
|
||||||
Тд |
= |
|
6 |
|
; |
|
6 |
|
|
|
||
|
3 2(1 + 10 |
|
|
|
|
|
|
|||||
Тд |
. 5) |
|
|
|
|
|
|
|||||
|
|
= 0,309 |
|
|
= |
Тп |
|
|
|
|
|
|
Скважность: |
|
|
и_эф |
|
|
|
|
|||||
Длительность импульса сигнала можно найти через эффективную площадь. Эффективная длительность сигнала
и_эф |
∫ |
∞ |
IТ |
; |
|
||||
и эф |
∞ |
|||
_ |
∑ |
|
д |
Тд . ` [ ] |
Параметр сигнала: |
|
= |
|
= 1.163 |
[ ] |
|
[ ] |
|
|
|
|||
Период дискретизации: |
Тд |
|
|
|
|
|
|||||||
|
Тд= |
иэф = 0.266 |
|
|
|
||||||||
Период повторения: |
|
|
Тп |
|
и |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
эф |
|
|
|
|
Тп |
|
|
|
|
|
повторения: |
|
|
|
|
|
||||
Количество отсчетов в периоде |
= 75.144 |
[Т] |
|
||||||||||
|
|
= |
|
|
|||||||||
д = 2 |
д = 5.404 [рад/с] |
|
|
|
= |
Тд = 0.86 |
с |
= |
д |
= 64 |
|||
Частота дискретизации: |
|
|
д |
|
|
|
|
||||||
Входной сигнал:t |
cos 0 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
S(t) e |
|
|
|
|
|
|
|
|
|
|
|
|

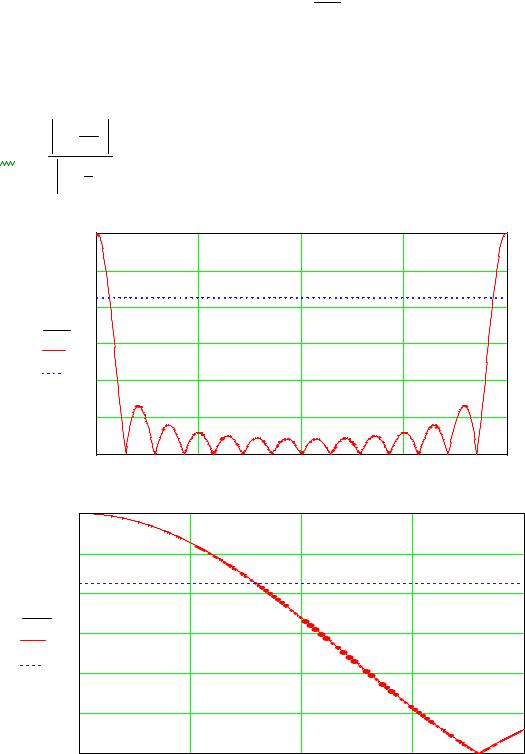
Количество отсчетов N=64 Дискретизированный сигнал:
|
Tä (n) |
|
|
n |
|
||
Sn e |
|
|
cos |
|
|
|
n 0 1 N 1 |
|
|
|
|||||
|
|
|
|
|
3 |
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sn |
10 |
20 |
0 |
1
n
Спектр дискретного сигнала:
S cfft(s)
0.8
Ssn 0.6
max(Ss)
0.707 0.4
0.2
0
0 |
20 |
40 |
60 |
n
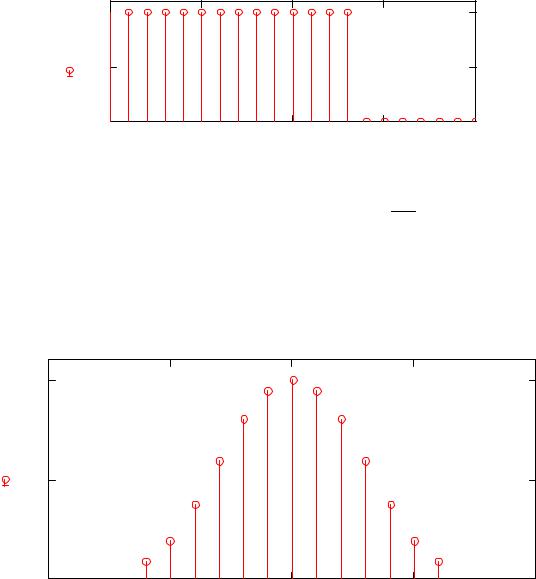
1.Приближенный расчет порядка фильтра (L) из анализа АЧХ однородного фильтра:
|
Частота среза: |
|
фильтра (при условии -3дБ по мощности): |
||||||
|
Порядок однородного |
||||||||
|
ср = ∆ Тд = 0.75 Тд |
= 0,232 |
|||||||
|
Отсюда получаем L=14опт = = |
ср |
= 14 |
|
|||||
|
|
2. |
Переходим к взвешиванию. |
|
|
|
|||
АЧХ однородного фильтра определяется следующим образом: |
|||||||||
|
|
|
L |
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
H( ) |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
sin |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0.833 |
|
|
|
|
|
|
|
|
H( ) |
0.667 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0.707 |
|
|
|
|
|
|
|
|
|
|
0.333 |
|
|
|
|
|
|
|
|
|
0.167 |
|
|
|
|
|
|
|
|
|
|
0 |
1.575 |
3.15 |
|
4.725 |
6.3 |
|
|
|
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0.833 |
|
|
|
|
|
|
|
|
|
0.667 |
|
|
|
|
|
|
|
H( ) |
|
|
|
|
|
|
|
||
L |
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0.707 |
|
|
|
|
|
|
|
||
|
|
0.333 |
|
|
|
|
|
|
|
|
|
0.167 |
|
|
|
|
|
|
|
|
|
|
0 |
|
0.125 |
0.25 |
|
0.375 |
0.5 |
|
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
Импульсная характеристика ФНЧ
|
L 1 |
n 0 1 N 1 |
h(n) |
|
(m n) |
m 0
1
hf(n)0.5
0
0 |
5 |
10 |
15 |
20 |
n
Окно Хэмминга:
Весовая функция задается на интервале: −  ÷
÷
Функция окна:
w(g) 0.53836 0.46164cos |
|
2 |
g |
|
|
|
|
||
|
||||
L 1
График весовой функции:
1
w(g)
0.5
0 |
5 |
0 |
5 |
10 |
10 |
g
Весовую функцию необходимо сдвинуть с таким расчетом, чтобы ее значение в нуле соответствовало середине окна.
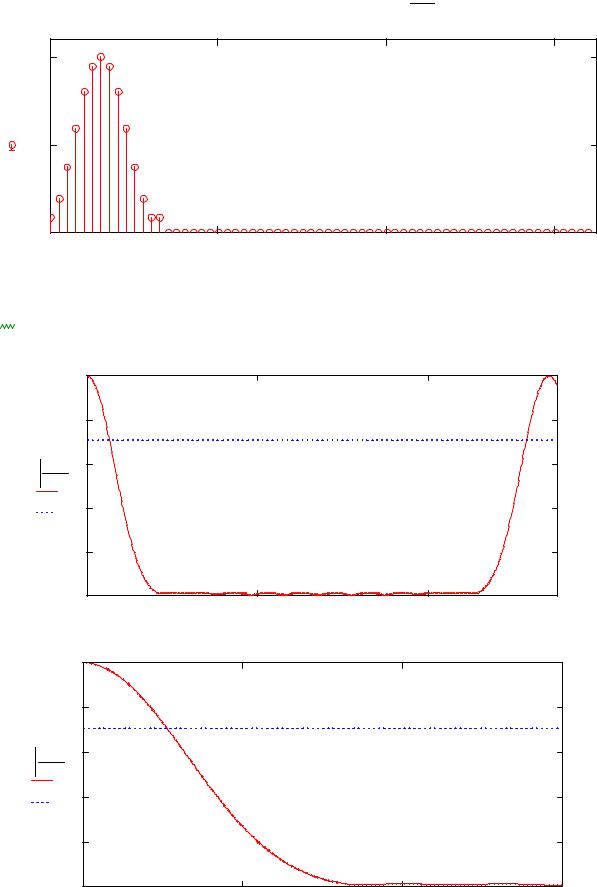
Импульсная характеристика фильтра с окном: |
|
||
h1(n) h(n) W(n u) |
|
//u= |
|
|
|
|
|
1 |
|
|
|
h(n) |
|
|
|
0.5 |
|
|
|
0 |
20 |
40 |
60 |
0 |
|||
|
|
n |
|
L 1 |
АЧХ фильтра с весовой функцией: |
|
|
i Td n |
|
|
|
|
|
|
|
H( ) h1(n) e |
|
|
|
n 0 |
|
|
|
0.8 |
|
|
|
H( ) 0.6 |
|
|
|
H(0) |
|
|
|
0.707 |
|
|
|
0.4 |
|
|
|
0.2 |
|
|
|
0 |
|
2 |
4 |
0 |
|
||
|
|
|
|
0.8 |
|
|
|
H( ) 0.6 |
|
|
|
H(0) |
|
|
|
0.707 |
|
|
|
0.4 |
|
|
|
0.2 |
|
|
|
0 |
0.5 |
1 |
1.5 |
0 |
|||
|
|
|
|
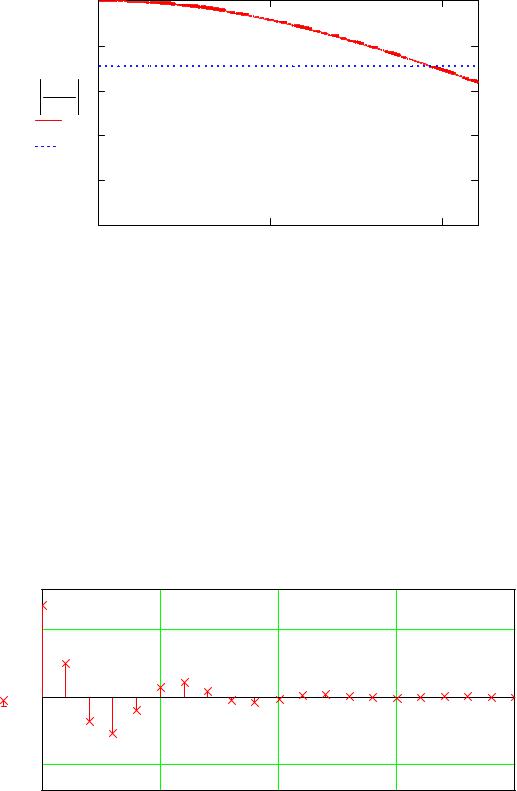
После взвешивания полоса пропускания увеличилась. Поэтому, чтобы добиться полосы пропускания, удовлетворяющей условию ТЗ, увеличим размер весовой функции.
При L=18, полоса пропускания удовлетворяет ТЗ:
0.8
H( ) 0.6
H(0)
0.707 0.4
0.2
0
0 |
0.1 |
0.2 |
Отклик фильтра на заданный сигнал:
|
L 1 |
yn |
h1(l) sn |
|
l 0 |
5
yn 0
5
0 |
5 |
10 |
15 |
20 |
n
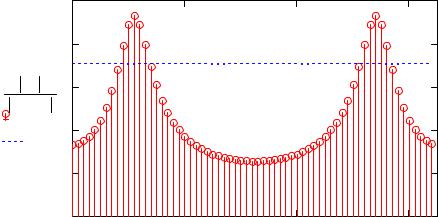
Спектр сигнала на выходе:
0.8
Yn 0.6
max(Y)
0.707 0.4
0.2
0
0 |
20 |
40 |
60 |
n
Выводы
Вданной работе с помощью БПФ был реализован фильтр с конечной импульсной характеристикой (КИХ). Они обладают рядом положительных свойств: они всегда устойчивы, они позволяют обеспечить совершенно линейную фазочастотную характеристику (постоянное время запаздывания).
Синтез фильтра производился методом окна. По заданию было задано окно Хэмминга.
Входе работы мы с помощью системы автоматизированного проектирования MathCad рассчитали: спектр входного сигнала, спектральную (амплитудно-частотную) характеристику окна, амплитудночастотную и импульсную характеристики фильтра, отклик фильтра на заданный сигнал, спектр выходного сигнала.
Частота дискретизации сигнала выбиралась исходя из условия обеспечения уровня неопределенности (наложения спектров) не хуже -13 дБ; Порядок фильтра (размер окна) определялся по следующему
алгоритму:
Из сопоставления заданной полосы фильтра и полосы сигнала определили порядок однородного фильтра L и приняли его в качестве первого приближения для размера «окна».
Построили АЧХ фильтра с заданной весовой функцией (промодифицировали последовательность h0(n) при помощи окна w(n), в результате получили требуемую импульсную характеристику h(n) конечной), оценили расширение полосы пропускания.
Скорректировали порядок фильтра в сторону увеличения для получения требуемой полосы пропускания.
Проанализировав полученный спектр сигнала на выводе и на входе видно, что сигнал прошел без искажений.
