1. Геометрические характеристики без ответов
.docx
|
Choice 35 |
0 |
#РАЗДЕЛ 1:# |
|
|
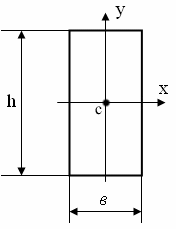
Оси х и у
проходят через центр тяжести сечения.
По какой формуле вычисляется момент
инерции относительно оси х J
|
|||
|
B·H3 12 |
|
||
|
B·H3 6 |
|
||
|
B·H2 12 |
|
||
|
B3· H 12 |
|
||
|
Choice 36 |
0 |
#РАЗДЕЛ 1:# |
|
|
Оси х и у
проходят через центр тяжести сечения.
По какой формуле вычисляется момент
сопротивления W
|
|||
|
B·H3 12 |
|
||
|
B·H2 6 |
|
||
|
B2·H 6 |
|
||
|
B2·H 12 |
|
||
|
Choice 37 |
0 |
#РАЗДЕЛ 1:# |
|
|
. Момент
инерции прямоугольника относительно
оси х равен Ј
|
|||
|
увеличится на величину
|
|
||
|
уменьшится на величину |
|
||
|
Останется прежней |
|
||
|
Будет равна нулю |
|
||
|
Choice 38 |
0 |
#РАЗДЕЛ 1:# |
|
|
Чему равен
момент инерции J
|
|||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Choice 39 |
0 |
#РАЗДЕЛ 1:# |
|
|
Точка с –
центр тяжести сечения. Чему равен
момент сопротивления W
|
|||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Choice 40 |
0 |
#РАЗДЕЛ 1:# |
|
|
Точка с –
центр тяжести сечения. Момент инерции
сечения J
|
|||
|
увеличится на величину
|
|
||
|
уменьшится на величину |
|
||
|
Будет равна нулю |
|
||
|
Останется прежней |
|
||
|
Choice 41 |
0 |
#РАЗДЕЛ 1:# |
|
|
Точка с –
центр тяжести сечения. Чему равен
центробежный момент инерции относительно
осей х
|
|||
|
J |
|
||
|
J |
|
||
|
J |
|
||
|
J |
|
||
|
Choice 42 |
0 |
#РАЗДЕЛ 1:# |
|
|
Точка с –
центр тяжести сечения. Чему равен
центробежный момент инерции относительно
осей х
|
|||
|
J |
|
||
|
J |
|
||
|
J |
|
||
|
J |
|
||
|
Choice 43 |
0 |
#РАЗДЕЛ 1:# |
|
|
На какой угол
нужно повернуть горизонтальную оси
х,у, чтобы новые оси х
|
|||
|
0 |
|
||
|
30 |
|
||
|
40 |
|
||
|
45 |
|
||
|
Choice 44 |
0 |
#РАЗДЕЛ 1:# |
|
|
Сумма моментов
инерции двутавра №22 (ГОСТ 8239-89)
относительно центральных осей х и у
равна 2550 + 157 = 2707 см
|
|||
|
Уменьшится |
|
||
|
Увеличится |
|
||
|
Останется прежней |
|
||
|
Будет равна нулю |
|
||
|
Choice 45 |
0 |
#РАЗДЕЛ 1:# |
|
|
Точка с – центр тяжести равнобокого уголка. На какой угол надо повернуть оси, чтобы они стали главными осями инерции?
|
|||
|
0 |
|
||
|
30 |
|
||
|
60 |
|
||
|
45 |
|
||
|
Choice 46 |
0 |
#РАЗДЕЛ 1:# |
|
|
Оси х, у, х
|
|||
|
Равна 0 |
|
||
|
Не меняется |
|
||
|
Возрастает |
|
||
|
уменьшается |
|
||
|
Choice 47 |
0 |
#РАЗДЕЛ 1:# |
|
|
По какой формуле определяется полярный момент инерции круглого сечения, диаметром d?
|
|||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Choice 48 |
0 |
#РАЗДЕЛ 1:# |
|
|
Какая формула справедлива для определения момента сопротивления круглого сечения, диаметром d?
|
|||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
Choice 49 |
0 |
#РАЗДЕЛ 1:# |
|
|
Оси х и у –
центральные оси инерции, А – площадь
сечения. Какая формула справедлива
для определения момента инерции
относительно оси х
|
|||
|
J |
|
||
|
J |
|
||
|
J |
|
||
|
J |
|
||
|
Choice 50 |
0 |
#РАЗДЕЛ 1:# |
|
|
Оси х и у –
центральные оси инерции, А – площадь
сечения. Какая формула справедлива
для определения момента инерции
относительно оси у
|
|||
|
J |
|
||
|
J |
|
||
|
J |
|
||
|
J у |
|
||
|
Choice 51 |
0 |
#РАЗДЕЛ 1:# |
|
|
Оси х и у
проходят через точку с – центр тяжести
сечения, А – площадь этого сечения.
Какая формула справедлива для
определения центробежного момента
инерции осей х
|
|||
|
J |
|
||
|
J |
|
||
|
J |
|
||
|
J |
|
||
|
Choice 52 |
0 |
#РАЗДЕЛ 1:# |
|
|
Момент
инерции прямоугольного сечения
относительно оси х определяется по
формуле: J
|
|||
|
Увеличится в 2 раза |
|
||
|
Увеличится в 6 раз |
|
||
|
Увеличится в 8 раз |
|
||
|
Увеличится в 4 раза |
|
||
|
Choice 53 |
0 |
#РАЗДЕЛ 1:# |
|
|
Во сколько
раз увеличится момент инерции
прямоугольника J
|
|||
|
2 |
|
||
|
4 |
|
||
|
8 |
|
||
|
16 |
|
||
|
Choice 54 |
0 |
#РАЗДЕЛ 1:# |
|
|
Как изменится
момент инерции прямоугольного сечения
относительно оси у (J
|
|||
|
уменьшится в 8 раз |
|
||
|
увеличится в 8 раз |
|
||
|
уменьшится в 2 раза |
|
||
|
увеличится в 2 раза |
|
||
|
Choice 55 |
0 |
#РАЗДЕЛ 1:# |
|
|
Во сколько
раз изменится момент инерции
прямоугольного сечения J
|
|||
|
2 |
|
||
|
8 |
|
||
|
12 |
|
||
|
4 |
|
||
|
Choice 56 |
0 |
#РАЗДЕЛ 1:# |
|
|
Относительно
какой горизонтальной оси момент
инерции сечения больше J
|
|||
|
J |
|
||
|
J |
|
||
|
J |
|
||
|
J |
|
||
|
Choice 57 |
0 |
#РАЗДЕЛ 1:# |
|
|
Чему равен
центробежный момент инерции J
|
|||
|
0 |
|
||
|
4вh |
|
||
|
|
|
||
|
|
|
||
|
Choice 58 |
0 |
#РАЗДЕЛ 1:# |
|
|
Во сколько
раз изменится момент сопротивления
W
|
|||
|
2 |
|
||
|
8 |
|
||
|
12 |
|
||
|
4 |
|
||
|
Choice 59 |
0 |
#РАЗДЕЛ 1:# |
|
|
Во сколько
раз изменится момент сопротивления
W
|
|||
|
2 |
|
||
|
4 |
|
||
|
6 |
|
||
|
8 |
|
||
|
Choice 60 |
0 |
#РАЗДЕЛ 1:# |
|
|
Во сколько раз изменится момент инерции J относительно оси х, если высота сечения изменится в 3 раза?
|
|||
|
3 |
|
||
|
9 |
|
||
|
27 |
|
||
|
4 |
|
||

 =?
=?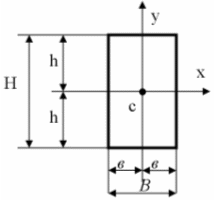
 сечения относительно оси х?
сечения относительно оси х?
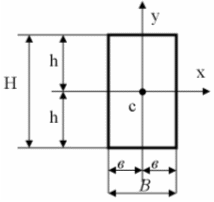
 =
=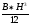 (см
(см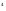 ).
Как изменится этот момент инерции,
если ось х
).
Как изменится этот момент инерции,
если ось х по нижней грани сечения?
по нижней грани сечения?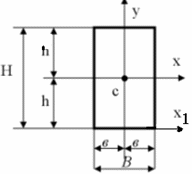
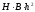

 сечения относительно оси у, если с –
центр тяжести сечения?
сечения относительно оси у, если с –
центр тяжести сечения?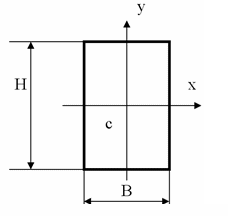
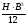
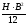
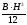
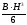
 относительно оси у?
относительно оси у?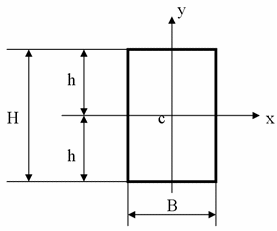
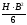
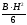
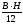
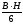
 относительно оси у равен J
относительно оси у равен J =
=
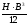 .
Как изменится эта величина, если
определять момент инерции относительно
оси у
.
Как изменится эта величина, если
определять момент инерции относительно
оси у J
J =
?
=
?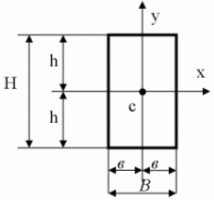
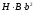
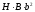
 ,у
,у ,
проведенных параллельно осям х, у
через точку К?
,
проведенных параллельно осям х, у
через точку К?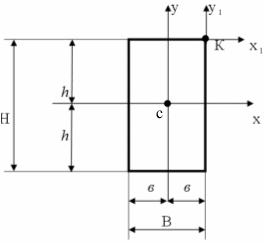
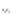 =H·B·h∙в
=H·B·h∙в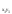 =
– H·B·h∙в
=
– H·B·h∙в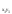 =
0
=
0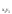 =
=
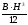
 ,у
,у ,
проведенных параллельно осям х, у
через точку К?
,
проведенных параллельно осям х, у
через точку К?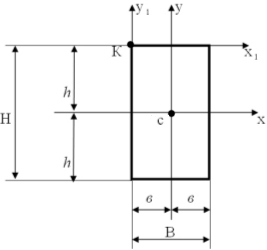
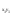 =H·B·h∙в
=H·B·h∙в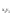 =
– H·B·h∙в
=
– H·B·h∙в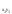 =
0
=
0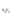 =
=
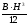
 ,у
,у стали главными?
стали главными?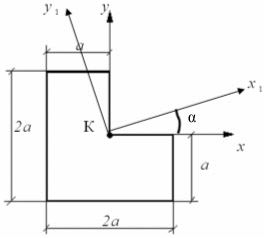




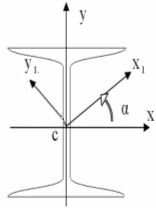
 .
Как изменится эта величина, если оси
повернуть на угол = 30
.
Как изменится эта величина, если оси
повернуть на угол = 30 ?
?
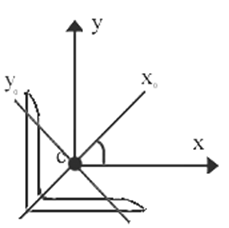




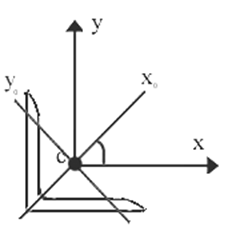
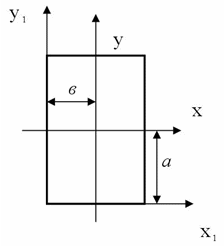
 ,
у
,
у проходят через точку с – центр тяжести
сечения. Какая зависимость между
суммой моментов инерции относительно
осей (J
проходят через точку с – центр тяжести
сечения. Какая зависимость между
суммой моментов инерции относительно
осей (J + J
+ J )
и (J
)
и (J + J
+ J )?
)?

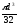
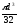
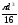
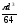
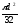
 ?
?
 =
J
=
J +
A∙a
+
A∙a =
J
=
J +
A∙a
+
A∙a =
J
=
J +
A∙a
+
A∙a
 =
J
=
J +
A∙в
+
A∙в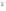
 ?
?
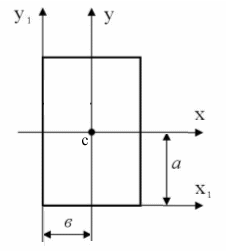
 =
J
=
J +
A∙a
+
A∙a =
J
=
J +
A∙a
+
A∙a =
J
=
J +
A∙a
+
A∙a
 = J у
+ A∙в
= J у
+ A∙в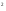
 ,у
,у ?
?
 =J
=J + A∙a∙в
+ A∙a∙в =J
=J +
A∙a
+
A∙a
 =J
=J +A∙в
+A∙в
 =J
=J +
J
+
J
 =
=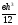 .
Как изменится момент инерции J
.
Как изменится момент инерции J ,
если ширина в увеличится в 2
раза?
,
если ширина в увеличится в 2
раза?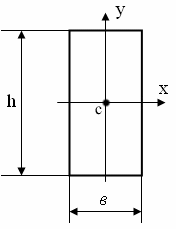
 ,
если размер h увеличить
в 2 раза?
,
если размер h увеличить
в 2 раза?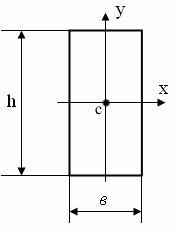
 ),
если размер в уменьшить в 2 раза?
),
если размер в уменьшить в 2 раза?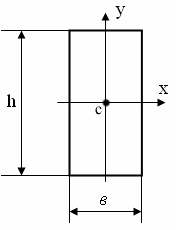
 относительно оси у, если высота h
изменится в 2 раза?
относительно оси у, если высота h
изменится в 2 раза?
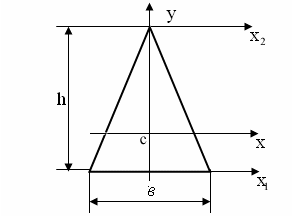
 ,J
,J ,J
,J ?
?




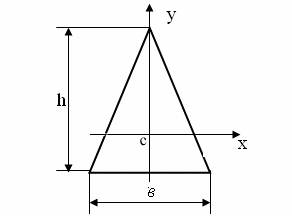
 равнобедренного треугольника?
равнобедренного треугольника?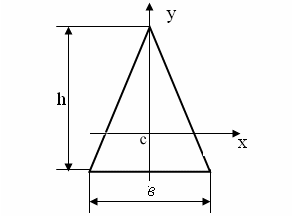

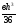
 относительно
оси х, если размер в изменить в 2
раза?
относительно
оси х, если размер в изменить в 2
раза?
 относительно
оси у, если размер в изменить в 2
раза?
относительно
оси у, если размер в изменить в 2
раза?