церебральноенасилие1
.docxТеоремы Коши и Лагранжа.
Существуют две теоремы: теорема Лагранжа и теорема Коши, устанавливающие связь между приращениями функций на некотором отрезке и значениями их производных в некоторой точке, лежащей внутри этого отрезка. Теорема Лагранжа была доказана раньше теоремы Коши и является частным случаем последней.
Теорема
Коши. Если
две функции f(x) и (x) непрерывны
на отрезке [a, b] и
дифференцируемы в промежутке (a, b),
причем производная /(x) второй
из них не обращается в нуль в этом
промежутке, то отношение конечных
приращений этих функций на
отрезке [a, b] равно
отношению их производных в некоторой
точке с промежутка (a, b) (быть
может не единственной): ![]()
Замечание. (b)-(a)0, так как иначе по теореме Ролля производная /(x) обращалась бы в нуль хотя бы в одной точке промежутка (a, b), а по теореме Коши /(x)0.
Теорема Лагранжа (о среднем): Конечное приращение на отрезке [a, b] функции, непрерывной на этом отрезке и дифференцируемой внутри него, равно произведению конечного приращения аргумента на этом отрезке на значение производной в некоторой внутренней точке с отрезка [a, b].
Рассмотрим, в чем состоит геометрический смысл теоремы Лагранжа:
![]() , но
, но ![]() -
это угловой коэффициент уравнения
хорды MN,
-
это угловой коэффициент уравнения
хорды MN,
соединяющей точки M и N графика функции y=f(x).
![]()
 С
другой стороны: правая часть формулы
равна угловому коэффициенту касательной
к этому графику в точке Р с
абсциссой x=c, где a<c<b.
С
другой стороны: правая часть формулы
равна угловому коэффициенту касательной
к этому графику в точке Р с
абсциссой x=c, где a<c<b.
|
|
|
|
Итак, формула устанавливает равенство угловых коэффициентов хорды и касательной, то есть параллельность хорды и касательной.
Таким образом, геометрический смысл теоремы Лагранжа заключается в следующем: на произвольной дуге графика дифференцируемой функции всегда найдется такая точка, в которой касательная к графику будет параллельна хорде, стягивающей концы дуги.
Физический смысл теоремы Лагранжа.
Пусть ![]() –
время, а
–
время, а ![]() –
координаты точки, движущейся по прямой,
в момент времени
–
координаты точки, движущейся по прямой,
в момент времени ![]() .
В выражении
.
В выражении
![]()
Величина
в левой части равенства является средней
скоростью движения точки по прямой за
промежуток времени от ![]() до
до ![]() .
Формула Лагранжа показывает, что
существует такой момент времени
.
Формула Лагранжа показывает, что
существует такой момент времени ![]() ,
в котором мгновенная скорость равна
средней скорости на временном отрезке
,
в котором мгновенная скорость равна
средней скорости на временном отрезке ![]() .
.
Если
в формуле Лагранжа положить ![]() ,
получим теорему Ролля, т. е. теорема
Ролля является частным случаем теоремы
Лагранжа.
,
получим теорему Ролля, т. е. теорема
Ролля является частным случаем теоремы
Лагранжа.
Положим
в формуле Лагранжа ![]() ,
, ![]() .
Тогда она примет вид
.
Тогда она примет вид
![]() ,
,
Где ![]() .
Данная формула связывает приращения
аргумента и функции, поэтому ее
называют Формулой
конечных приращений.
Данная формула дает точное выражение
приращения функции через вызвавшее его
приращение аргумента в отличие от
дифференциала функции, который определяет
приближенное значение приращения
функции:
.
Данная формула связывает приращения
аргумента и функции, поэтому ее
называют Формулой
конечных приращений.
Данная формула дает точное выражение
приращения функции через вызвавшее его
приращение аргумента в отличие от
дифференциала функции, который определяет
приближенное значение приращения
функции: ![]() .
В приближенных вычислениях приращение
функции заменяют чаще дифференциалом,
т. е. полагают
.
В приближенных вычислениях приращение
функции заменяют чаще дифференциалом,
т. е. полагают ![]() .
Формула Лагранжа применяется реже, так
как для ее использования необходимо
указать точку
.
Формула Лагранжа применяется реже, так
как для ее использования необходимо
указать точку ![]() ,
что, вообще говоря, не всегда удается.
,
что, вообще говоря, не всегда удается.
Обобщением теоремы Лагранжа является теорема Коши.
Пример Коши

Пример Лагранжа

Теорема
Ролля о нулях производной. Если функция
f(x) непрерывна на отрезке [a,b], дифференцируема
на интервале (a, b) и принимает в концах
этого отрезка равные значения, т.е.
f(a)=f(b) (1), то существует точка ![]() такая что
такая что ![]() (2).
(2).
Геометрический
смысл т. Ролля: при условиях теоремы
существует значение ![]() такое,
что касательная к графику функции y=f(x)
в точке
такое,
что касательная к графику функции y=f(x)
в точке ![]() параллельна
оси Ox.
параллельна
оси Ox.
Замечание. Все условия т. Ролля существенны.

Теорема Ферма
Если
функция ![]() имеет
производную и в точке
имеет
производную и в точке ![]() имеет
экстремум, то значение производной в
этой точке равно 0.
имеет
экстремум, то значение производной в
этой точке равно 0.
|
|
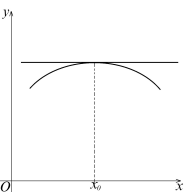
Геометрический смысл теоремы Ферма Существует
такая точка Замечания
|
-
Равность нулю производной - необходимое условие существования экстремума, но не достаточное. То есть производная может быть равной 0 и вне точки экстремума. Пример:
 ,
но точка 0 - не экстремум.
,
но точка 0 - не экстремум.
Пример