matan_test_otvety

---------------------------------------------------------

Найти наименьшее значение функции на отрезке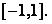

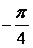-- True

---------------------------------------------------------

---------------------------------------------------------

Вычислить неопределенный интеграл

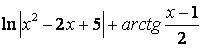-- True

---------------------------------------------------------

0 -- True

---------------------------------------------------------

Вычислить неопределенный интеграл

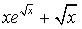-- False

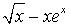-- False

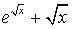-- False

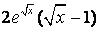-- True

-- False

---------------------------------------------------------

Применяя логарифмическое дифференцирование, найти производную следующей функции:

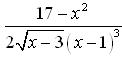-- True

---------------------------------------------------------

Найти производную 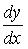от следующей параметрически заданной функции:

-- False

-- False

-- True

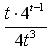-- False

-- False

---------------------------------------------------------

5 -- True

---------------------------------------------------------

Найти наименьшее значение функции на отрезке [-5,12].

5 -- True

---------------------------------------------------------

Найти дифференциал 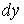от следующей функции:

-- True

---------------------------------------------------------

Найти производные второго порядка от следующих функций:

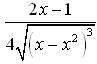-- True

---------------------------------------------------------

-- True

---------------------------------------------------------

Вычислить неопределенный интеграл

-- True

7.3.1. Если предел не существует, то это означает, что:

Варианты ответа:

#1) не имеет производной в точке x0;

2)неограничена в точке x0;

3)имеет разрыв в точке x0;

4)не имеет обратной функции в точке x0;

5)имеет обратную функцию в точке x0.

7.3.2. выражает Варианты ответа:

1)среднюю скорость изменения функции f на отрезке [x0; x0 + Dx];

2)ординату пересечения кривой y = f(x) с осью 0y;

#3) мгновенную (или предельную) скорость изменения функции f(x) в точке x0;

4)угловой коэффициент касательной к кривой y = f(x) в точке с абсциссой x0;

5)абсциссу пересечения y = f(x) с осью 0х.

7.3.3. Если f(x) всюду дифференцируемая нечетная функция, тогда

Варианты ответа:

1) функция f ?(x) является нечетной; #2) функция f ?(x) является четной;

3)f ?(?x) = ? f ?(x);

4)функция f ?(x) является периодической;

5)имеет обратную функцию в точке x0 .

7.3.4. Если f(x) всюду дифференцируемая периодическая функция, тогда

Варианты ответа:

1)функция f ?(x) является нечетной;

2)f ?(?x) = ? f ?(x);

3)функция f ?(x) является четной;

#4) функция f ?(x) является периодической; 5) имеет обратную функцию в точке x0 .

7.3.5. Если функция f(x) дифференцируема в точке x0 , то угловой коэффициент касательной к графику функции y = f(x) в точке с абсциссой x0 равен

Варианты ответа:

1)f(x0);

2)f ?(x0)?x;

3);

4);

#5) .

7.3.6.Уравнение касательной к графику функции y = f(x) в точке с абсциссой x0 имеет

вид:

Варианты ответа:

1) y = f ?(0)(x ? x0) + f(0); #2) y = f ?(x0)(x ? x0) + f(x0); 3) y ? f(x0) = f ?(x0)(x ? y0); 4) y + f(x0) = f ?(x0);

5) y = x f ?(x0) + f(x0) .

7.3.7.Если функции u(x) и v(x) дифференцируемы в точке x0, то

Варианты ответа:

#1) частное этих функций также дифференцируемо в точке x0 (при условии v(x0) ? 0), причем в этой точке справедливо равенство ;

2)частное этих функций также дифференцируемо в точке x0 (при условии v(x0) ? 0), причем в этой точке справедливо равенство ;

3)частное этих функций также дифференцируемо в точке x0 (при условии

v(x0) ? 0), причем в этой точке справедливо равенство ;

4)частное этих функций также дифференцируемо в точке x0 (при условии v(x0) ? 0), причем в этой точке справедливо равенство ;

5)частное этих функций может быть не дифференцируемым в точке x0.

7.3.8.Если функция x = ?(t) дифференцируема в точке t0, а функция f(x) дифференцируема в точке x0 = ?(t0), то

Варианты ответа:

1) сложная функция y(t) = f(?(t)) дифференцируема в точке t0, при этом ; 2) сложная функция y(t) = f(?(t)) дифференцируема в точке t0, при этом ;

3) сложная функция y(t) = f(?(t)) может быть не дифференцируемой в точке t0. #4) сложная функция y(t) = f(?(t)) дифференцируема в точке t0, при этом ;

5) сложная функция y(t) = f(?(t)) дифференцируема в точке t0, при этом .

7.3.9.Пусть функция y = f(x) возрастает (убывает) на промежутке X и имеет отличную от нуля производную в точке x0 из этого промежутка. Тогда обратная ей функция x = f ?1(y)

Варианты ответа:

1)имеет производную в точке y0 = f(x0), причем эта производная равна ;

2)может не иметь производной в точке y0 = f(x0).

3)имеет производную в точке y0 = f(x0), причем эта производная равна ;

4)имеет производную в точке y0 = f(x0), причем эта производная равна ; #5) имеет производную в точке y0 = f(x0), причем эта производная равна .

7.3.10. Если функции u(x), r(x) и v(x) дифференцируемы в точке x0, то и функция дифференцируема в точке x0 (при условии r(x0) ? 0), причем в этой точке справедливо равенство

Варианты ответа: 1) ; #2) ;

3);

4);

5).

7.3.11. Если функции u(x), r(x) и v(x) дифференцируемы в точке x0, то и функция дифференцируема в точке x0, причем в этой точке справедливо равенство

Варианты ответа: #1) ;

2);

3);

4);

5).

7.3.12. Если функции u(x), r(x) и v(x) дифференцируемы в точке x0, то и функция дифференцируема в точке x0 (при условии r(x0) ? 0), причем в этой точке справедливо равенство

Варианты ответа:

1);

2);

#3) ;

4);

5).

7.3.13. Дифференциал отношения двух функций равен Варианты ответа:

1) ; #2) ;

3);

4);

5).

7.3.14. Пусть функция f(x) непрерывна на отрезке ?a; b? и дифференцируема на интервале (a; b), причем f(a) = f(b). Этих условий достаточно, чтобы утверждать, что на интервале (a; b)

Варианты ответа:

1)существует ровно две стационарные точки функции f(x);

2)существует ровно одна стационарная точка функции f(x);

3)не существует стационарной точки функции f(x);

#4) существует хотя бы одна стационарная точка функции f(x); 5) существует не более одной стационарной точки функции f(x).

7.3.15. Пусть функции f(x) и g(x) непрерывны на отрезке ?a; b? и дифференцируемы на интервале (a; b), причем g?(x) ? 0 в каждой точке x этого интервала. Тогда существует точка c ? (a; b) такая, что

Варианты ответа:

1);

2);

#3) ;

7.3.16.Известно, что функция f(x) непрерывна на отрезке ?a; b? и дифференцируема на интервале (a; b). Этих условий достаточно, чтобы утверждать

Варианты ответа:

1) в этом интервале не существует стационарная точка функции f(x); #2) в этом интервале существует такая точка c, что ;

3) внутри отрезка ?a; b? найдется точка, в которой касательная, проведенная к графику функции y = f(x), будет перпендикулярна прямой, проходящей через точки (a, f(a)) и (b, f(b));

4) внутри этого отрезка всегда найдется точка, в которой касательная, проведенная к графику функции y = f(x), будет параллельна оси Ox;

5) внутри этого отрезка всегда найдется точка, в которой касательная, проведенная к графику функции y = f(x), будет параллельна оси Oy.

7.3.17.Функция f(x) возрастающая функция на промежутке X, если f(x) непрерывна на промежутке X и

Варианты ответа:

1)имеет нулевую производную во всех внутренних точках этого промежутка;

2)имеет неположительную производную во всех внутренних точках этого промежутка, причем внутри промежутка X нет такого интервала, в каждой точке которого производная равнялась бы нулю; #3) имеет неотрицательную производную во всех внутренних точках этого промежутка,

причем внутри промежутка X нет такого интервала, в каждой точке которого производная равнялась бы нулю;

4)имеет отрицательную производную во всех внутренних точках этого промежутка;

5) не существует производной функции во всех внутренних точках этого промежутка.

7.3.18. Функция f(x) убывающая функция на промежутке X, если f(x) непрерывна на промежутке X и

Варианты ответа:

#1) имеет неположительную производную во всех внутренних точках этого промежутка, причем внутри промежутка X нет такого интервала, в каждой точке которого производная равнялась бы нулю;

2)имеет нулевую производную во всех внутренних точках этого промежутка;

3)имеет неотрицательную производную во всех внутренних точках этого промежутка, причем внутри промежутка X нет такого интервала, в каждой точке которого производная равнялась бы нулю;

4)имеет положительную производную во всех внутренних точках этого промежутка;

5) не существует производной функции во всех внутренних точках этого промежутка.

7.3.19. Многочлен Тейлора Tn(x) n-го порядка для функции f(x) в точке x0 имеет вид

Варианты ответа:

1);

2);

#4) ;

5).

7.3.20. Формула Тейлора n-го порядка для функции f(x) в точке x0 с остатком n-го порядка в форме Пеано имеет вид

4), где с ? (x0; x).

5), где с ? (x0; x).

7.3.21. Формула Тейлора n-го порядка для функции f(x) в точке x0 с остатком n-го порядка в форме Лагранжа имеет вид Варианты ответа:

1)F1(x) = С ? F2(x), где С - некоторая константа;

2)F1(x) + F2(x) = С, где С - некоторая константа; #3) F1(x) – F2(x) = С, где С - некоторая константа;

4)F1(x) = , где С - некоторая константа;

5)F1(x) = , где С - некоторая константа.

7.4.4. Пусть F(x) произвольная первообразная для функции f(x) на промежутке (–?; +?). Тогда:

Варианты ответа:

1)если f(x) - четная функция, то F(x) - нечетная функция;

2)если f(x) - нечетная функция, то F(x) - нечетная функция;

3)если f(x) - периодическая функция, то и F(x)- периодическая функция;

4)если f(x) - четная функция, то F(x) - четная функция;

#5) если f(x) - нечетная функция, то F(x) - четная функция.

7.4.5. Множество функций {arcsin x + C} задается неопределенным интегралом вида:

Варианты ответа:

1);

2);

#3) ;

4);

5).

7.4.6. Из приведенных интегралов выберите ?неберущиеся? интегралы:

Варианты ответа: #1) ;

2);

3).

4);

5).

7.4.7.Укажите верные равенства: Варианты ответа:

1) ;

2) ; #3) ; 4) ; 5) .

7.4.8.Укажите верные равенства: Варианты ответа:

1)

#2)

3)

4)

5)