Основные свойства несобственных интегралов.

На несобственные интеграла распространяются многие свойства определенных интегралов. Пусть F(x) – первообразная от f(x). Тогда

П р и м е р .

.

Следовательно, интеграл сходится при p > 1 и расходится при p≤ 1.

y

p < 1

1 p = 1

0 1 x

p > 1

Признаки сходимости несобственных интегралов.

1. Если 0 ≤ f(x) ≤ φ(x) и

2. Если 0 ≤ φ (x) ≤ f(x) и

Для сравнения, как правило, используются интегралы

П р и м е р ы .

1. 

2. 

В предыдущих примерах рассматривались интегралы от неотрицательных функций. Если f(x) произвольного знака, то применяется следующий признак

3. Если

В этом случае интеграл (**) называется абсолютно сходящимся.

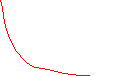
П р и м е р

Интеграл от неограниченной функции.

Пусть функция f(x) непрерывна в интервале [a, b], а при x = b обращается в бесконечность. f(b) = ∞. Обобщим понятие определенного интеграла на такую функцию.

y

a b-ε b x

Возьмем значение ε > 0 и найдем интеграл .

Найдем предел - несобственный интеграл от неограниченной функции f(x) на промежутке [a, b).

Если этот предел существует, то интеграл называется сходящимся, в противном случае интеграл называется расходящимся.

Аналогично определяются и другие несобственные интегралы от неограниченной функции.

Пусть f(x) - непрерывна в промежутке (a, b], а в точке x = a обращается в бесконечность.

y

x

a a+ε b

Пусть функция f(x) непрерывна в интервалах [a, c) и (c, b], а f(c) = ∞. Тогда

y

a c-ε₁ c c+ε₂ b x

П р и м е р 1

.Все свойства, рассмотренные для интеграла , переносятся и на интеграл от неограниченных функций. Для сравнения следует брать функции

Интегралы, зависящие от параметра.

Рассмотрим интеграл вида

Здесь λ – параметр, т.е. величина, которая в процессе интегрирования остается постоянной. но может принимать различные значения. Интеграл является функцией параметра λ.

П р и м е р ы .

1. 

2. 

Дифференцирование интегралов, зависящих от параметра.

1. Предположим, что f(x, λ) и f′_λ (x, λ) − непрерывные функции при

c ≤ λ ≤ d, a ≤ x ≤ b.

Найдем производную от интеграла по параметру λ.

.

Последняя формула называется формулой Лейбница.

2. Предположим, что в интеграле (1) пределы интегрирования тоже зависят от параметра λ.

(2)

Можно показать, что производная от интеграла (2) по параметру α имеет вид

С помощью формулы Лейбница можно вычислить некоторые определенные интегралы.

П р и м е р 1. Вычислить интеграл

Интеграл не берется.

Остается определить С. Для этого заметим, что

Подставив в равенстве (*) λ = 0, получим 0 = arctg 0 + C. Отсюда С = 0.

Следовательно, для любого значения λ имеет место равенство I(λ) = arctg λ, т.е.

П р и м е р 2 . Гамма-функция. Это неэлементарная функция, введенная Эйлером в 1729 г.

(1)

Покажем, что этот несобственный интеграл сходится при p > 0. Представим интеграл в виде суммы

Первый интеграл в правой части – это интеграл от неограниченной функции, если p - 1 < 0. Он сходится, т.к. 0 < e^-x ≤ 1 и

Второй интеграл тоже сходится. Действительно, пусть n – целое число, такое, что n > p – 1. Тогда, очевидно,

Рассмотрим интеграл . Вычисляя этот интеграл n раз по частям с учетом того, что

(2)

можно доказать, что он сходится. Следовательно, интеграл (1) сходится при p > 0.

Эта функция часто используется в приложениях. Найдем значения Γ(p) при целых p. При p = 1 имеем

Пусть p > 1. интегрируем по частям

u = x ^{p – 1}, d v = e ^–xdx,

du = (p – 1)x ^{p – 2}dx

Γ(p)

Γ(2) = 1, Γ(3) = 2∙1 = 2!, Γ(4) = 3∙Γ(3) = 3∙2∙1 = 3!, .... Γ(n) = (n – 1)!