
- •Задача о площади криволинейной трапеции.
- •Формула Ньютона-Лейбница.
- •Интегрирование по частям.
- •Замена переменной под знаком определенного интеграла.
- •Объем тела с известным поперечным сечением.
- •Объем тела вращения.
- •Интеграл с переменным верхним пределом.
- •Несобственные интегралы.
- •Основные свойства несобственных интегралов.
- •Признаки сходимости несобственных интегралов.
- •Интеграл от неограниченной функции.
- •Интегралы, зависящие от параметра.
Определенный интеграл.
Задача о площади криволинейной трапеции.
Рассмотрим фигуру, ограниченную кривой
y = f(x), прямыми x = a, x = b и отрезком оси оx a ≤ x ≤ b. Эта фигура называется криволинейной трапецией. Разобьем промежуток [a, b] на n произвольных частей, в каждом частичном промежутке возьмем точку ξi (xi ≤ ξi ≤ xi+1) и найдем ∆Si = f(ξi)(xi+1 – xi) = f(ξi) ∆xi
Площадь ступенчатой фигуры запишется
![]()
![]()
Эта сумма тем точнее характеризует площадь криволинейной трапеции, чем меньше ∆xi.
Поэтому за истинное значение площади принимают предел
![]()
Этот предел, если он существует, если он не зависит от способа разбиения интервала [a, b] на частичные и от выбора точек ξi, называется определенным интегралом от функции f(x) по промежутку [a, b].
Функцию f(x) называют в этом случае интегрируемой на [a, b].
Sn – интегральная сумма.
Очевидно,
![]()
Теорема существования.
Если функция f(x) непрерывна на промежутке [a, b], то она и интегрируема на этом промежутке.
Формула Ньютона-Лейбница.
Пусть f(x) – непрерывна на [a, b], F(x) – первообразная, т.е. F′(x) = f(x).
Разобьем промежуток [a, b] на n произвольных частей.
F(b) – F(a) = F(x1) – F(x0) + F(x2) – F(x1) + F(x3) – F(x2) + … + F(xn) – F(xn-1) =

П р и м е р . Вычислить площадь, ограниченную одной аркой синусоиды и осью абсцисс.
 y
y ![]()
 y
= sin x
y
= sin x

-
π

Свойства определенного интеграла.

4. Для любых трех чисел a, b, c справедливо равенство
![]()
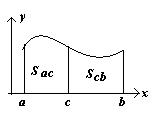
Геометрическая иллюстрация.
-
a < c < b . Sab = Sac + Scb 2. a < b < c. Sab = Sac - Sbc
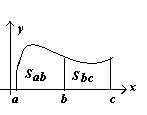
5. Если f(x)
> 0 и a < b,
то
![]()
Если f(x)
< 0 и a < b,
то
![]()
Пусть f(x) > 0, a < b, F(x) – первообразная f(x), F′(x) = f(x) > 0, следовательно, F(x) возрастает, т.е. F(b) > F(a).
![]()
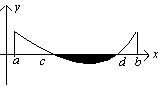
Эту теорему следует учитывать при вычислении площадей криволинейных трапеций.
-
f(x) ≥ 0.
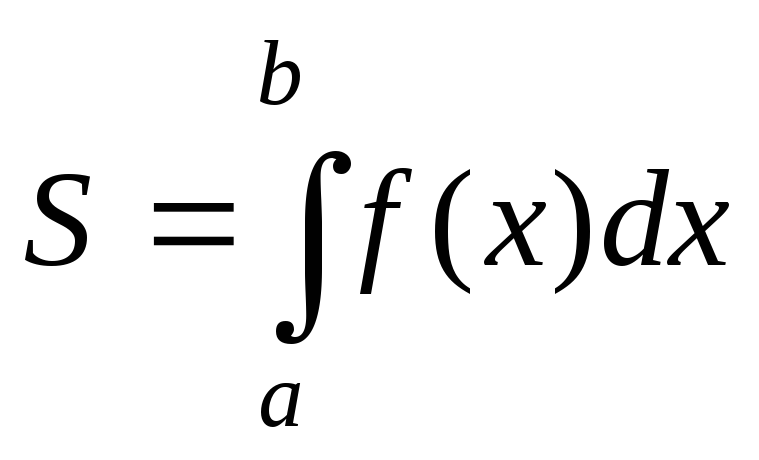
f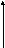

 (x)
(x)

 a b
x
a b
x
-
f
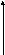 (x)
≤ 0.
(x)
≤ 0.
![]()


 a
b x
a
b x


З а д а ч и .
Вычислить площадь, ограниченную кривыми.

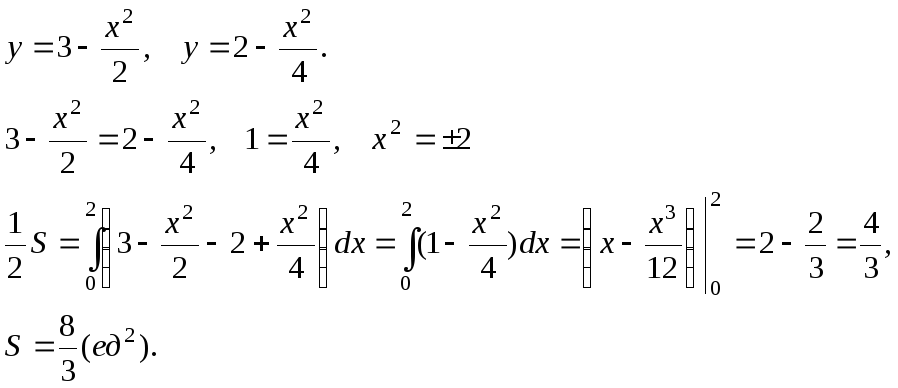
-
y = x2 – 1, x + y – 1 = 0.

 y
y

 x2
– 1 = 1 – x, x2 –
x – 2 = 0
x2
– 1 = 1 – x, x2 –
x – 2 = 0
 y = 1 - x
y = 1 - x
x1 = 1, x2 = -2 .

 -2
1 x
-2
1 x
y = x2 - 1
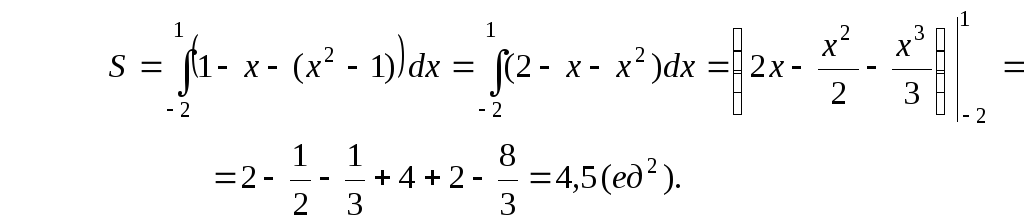
Интегрирование по частям.



 d(uv) = du∙v + u∙dv, u
dv = d(uv) – v du
d(uv) = du∙v + u∙dv, u
dv = d(uv) – v du
![]()
![]() .
.
П р и м е р .

Замена переменной под знаком определенного интеграла.
Пусть требуется вычислить
![]() Введем новую переменную t
по формуле
x =
φ(t).
Введем новую переменную t
по формуле
x =
φ(t).
Если
-
φ(α) = a, φ(β) = b,
-
φ(t) – непрерывная монотонная функция на интервале [α, β], то

 x
x



 b
b



 a φ(β)=b
4
a φ(β)=b
4


φ(α)=a



 α
β t 0 2
t
α
β t 0 2
t
П р и м е р 1 .
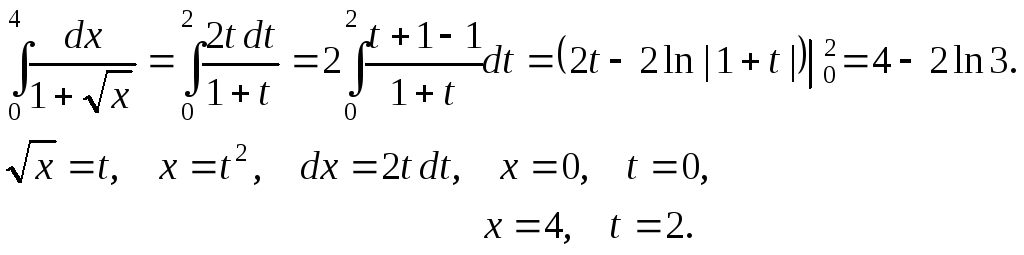
П р и м е р 2 . Вычислить площадь, ограниченную эллипсом x = a cos t, y = b sin t.
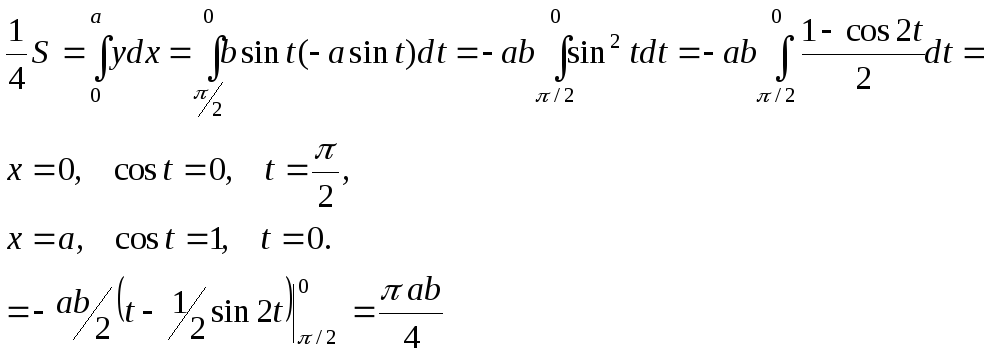
 y
y


 a
a x
a
a x
