
- •7.3.12. Если функции u(X), r(X) и V(X) дифференцируемы в точке x0, то и функция дифференцируема в точке x0 (при условии r(x0) ? 0), причем в этой точке справедливо равенство
- •4.1.2. Lim (X-sinx) / (X-tgx) .
- •4.1.17. Lim(e -1-X)/(sinx) .
- •4.1.18. Lim(sinx-xcosx)/X .
- •4.1.21.Lim((1/X)-(1/sinx)) .
- •4.1.31. Lim(ctgx -1)/(sin4x).
- •7.3.2. Выражает
- •7.3.3. Если f(X) всюду дифференцируемая нечетная функция, тогда
- •7.3.4. Если f(X) всюду дифференцируемая периодическая функция, тогда
- •7.3.7. Если функции u(X) и V(X) дифференцируемы в точке x0, то
4.1.2. Lim (X-sinx) / (X-tgx) .
Варианты ответа:
#5) -1/2.
4.1.3. lim x e. стремиться к - бесконечности
Варианты ответа:
#1) 0;
4.1.4. lim x стремиться к 0.
Варианты ответа:
#2) 1;
4.1.5. lim(lnx) .
Варианты ответа:
#2) 1;
4.1.6. lim(e -e -2x)/(x-sinx).
Варианты ответа:
#3) 2;
4.1.7. lim (x +3x -9x+5)/(x-x-x+1) Варианты ответа:
#4) 3;
4.1.8.limxln x
Варианты ответа:
#1) 0;
4.1.9.lim(ctgx-1/x) .
Варианты ответа:
#1) 0;
4.1.10.lim(cosx) .
Варианты ответа:
1) 1;
x 1/x
4.1.11. lim(e +x).
Варианты ответа:
#2) e;
4.1.12.lim(x-arctgx)/x .
Варианты ответа:
#3) 1/3 ;
4.1.13. (6e -x-3x-6x-6)/(2cos+x-2).
Варианты ответа:
#4) 3;
4.1.14. lim(x e ).
Варианты ответа: #1) 0;
4.1.15. lim x .
Варианты ответа:
#2) 1;
4.1.16. lim (1/x).
Варианты ответа:
#2) 1;
4.1.17. Lim(e -1-X)/(sinx) .
Варианты ответа:
#4) 1/2;
4.1.18. Lim(sinx-xcosx)/X .
Варианты ответа:
#4) 1/3;
4.1.19.lim(lnx)/(ctg2x) .
Варианты ответа: #1) 0;
4.1.20.lim(1/lnx)-(1/x-1) .
Варианты ответа:
#3) 1/2;
4.1.21.Lim((1/X)-(1/sinx)) .
Варианты ответа:
#1) 0;
4.1.22.limx(e -1).
Варианты ответа:
#2) 1;
4.1.23.lim(1/x) .
Варианты ответа:
#3) 1;
4.1.24.(sin2x).корень(x+1)-1 .
Варианты ответа:
#4) 4;
4.1.25.((sinx)/(x)) .
Варианты ответа:
#3) 1;
4.1.26. lim(e -1)/(arctg3x).
Варианты ответа:
#5) 5/3.
4.1.27.lim(ln x)/(e ).
Варианты ответа:
#5) 0.
4.1.28. lim(sinx-tgx) .
Варианты ответа:
#4) -1/2 ;
4.1.29. lim(Пи-2arctgx)/(e -1).
Варианты ответа:
#2) 1;
4.1.30. lim (x-4x+5x)/(x-5x+7x-3) .
Варианты ответа:
#1) 1/2 ;
4.1.31. Lim(ctgx -1)/(sin4x).
Варианты ответа:
#4) 1/2 ;
4.1.32.lim(tg Пи/2x)/(ln(1-x)) .
Варианты ответа:
#5) минус бесконечность.
4.1.33. lim(lnx)/(x ).
Варианты ответа:
#3) 0;
4.1.34.lim(Пи-x)tg x/2 .
Варианты ответа:
#3) 2;
4.1.35.lim(lnx)/(5+3lnsinx) .
Варианты ответа:
#4) 1/3 ;
4.1.36. lim(1/lnx)-(x/lnx) .
Варианты ответа:
#4) -1;
4.1.37. lim(1/x)-(1/arctgx) .
Варианты ответа: #1) 0;
4.1.38.lim(sinx) .
Варианты ответа:
#2) 1;
4.1.39.lim(arcsinx) .
Варианты ответа:
#3) 1;
4.1.40.lim(arcsinx ) .
Варианты ответа:
#2) 1;
4.1.41. lim(ctgx) .
Варианты ответа:
#5) 1/e .
4.1.42. lim(tgx) .
Варианты ответа:
#3) e ;
4.1.43. lim(x+5 ).
Варианты ответа:
#5) 5 .
4.1.44.lim(x +x-10)/(x -3x-2).
Варианты ответа:
#1) 13/9 ;
4.1.45.limx sin1/x .
Варианты ответа:
#2) 1;
4.1.46.lim(sinx)/(sin2) .
Варианты ответа:
#4) e ;
4.1.47.lim(e -e +x)/(sin3x).
Варианты ответа: #1)1/3 ;
4.1.48.lim(sinx-cosx)/(ln(tgx) Варианты ответа:
#2)корень2/2 ;
4.1.49.lim (x+5x +8x+4)/(x +3x-4).
Варианты ответа:
#1) 1/3 ;
4.1.50. lim (x -3x+2)/(x -2x+1).
Варианты ответа
#3) 2/5;
Тейлор
4.2.1. Написать многочлен Тейлора 2-го порядка для функции y=ln x при x0=3
* ln3+1/3(x-3)-1/18(x-3)2+о((x-3)3)
4.2.2. Найти коэффициент a1 многочлена Тейлора для функции y=корень3x-2 при x0=1
* 3/2
4.2.3. Написать многочлен Тейлора 2- й степени для функции y=cos2x при x0=0
* 1-2x2+о(x3)
4.2.4.Написать многочлен Тейлора 2- й степени для функции y=ex2 при x0=0
* 1+x2+о(x3)
4.2.5. Многочлен 2x3-3x2+5x+1 разложить по степеням двучлена x+1 .
* -9+17(x+1)-9(x+1)2+2(x+1)3
4.2.6. Разложить многочлен x3+3x2+2x-5 по степеням двучлена x+2 .
* (x+2)3-3(x+2)2+2(x+2)-5
4.2.7. Разложить функцию f(x)=x3-x-1 по степеням x-1 , пользуясь формулой Тейлора.
* -1+2(x-1)+3(x-1)2+(x-1)3
4.2.8. Найти коэффициент многочлена Тейлора a1 для функции y=arcsinx при x0=0
* 1
4.2.9. Написать многочлен Тейлора 1- го порядка для функции y=корень4-x при x0=0
* 2-x/4+о(x2)
4.2.10. Написать многочлен Тейлора 2-го порядка для функции y=e в степени x2-4 при x0=4
* 1+4(x-2)+9(x-2)2+о((x-2)3)
4.2.11. Вычислить приближенно ln1,05
*0,05 x+2
4.2.12. Разложить многочлен x2-5x+7 по степеням двучлена x+2 .
* 21-9(x+2)+(x+2)2
4.2.13. Разложить функцию f(x)=x2+2x-5 по степеням x-1 , пользуясь формулой Тейлора.
* -2+(x-1)+(x-1)2
4.2.14. Получить многочлен Тейлора 2-го порядка для функции y=arctgx при x0=0
* П/4+1/2(x-1)-1/4(x-1)2+о((x-1)3)
4.2.15.Написать многочлен Тейлора 2- го порядка для функции y=x2lnx при x0=1
* x2lnx=(x-1)+3/2(x-1)2+о(x-1)3
4.2.16. Написать многочлен Тейлора 2-го порядка для функции y=cos степень 2 потом x при x0=0
* cos степень 2 потом x =1-x2+o(x3)
4.2.17. Вычислить приближенно 1/корень 3 степени от e
* 0,722
![]()
 --
True
--
True
---------------------------------------------------------
![]()
![]() --
True
--
True
---------------------------------------------------------
 С
помощью
таблицы
и
правил
дифференцирования
арифметических
операций
найти
производную
следующей
функции:
С
помощью
таблицы
и
правил
дифференцирования
арифметических
операций
найти
производную
следующей
функции:
-- True
---------------------------------------------------------

![]()
---------------------------------------------------------
Найти
производные
второго
порядка
![]() от
следующих
функций:
от
следующих
функций:
![]()

---------------------------------------------------------
Найти
производное
![]() от
следующей
неявной
функции:
от
следующей
неявной
функции:
 --
True
--
True
---------------------------------------------------------
Вычислить неопределенный интеграл
![]()
 --
True
--
True
---------------------------------------------------------
![]()

![]()
---------------------------------------------------------
Найти
точку
минимума
функции
![]()
![]()
---------------------------------------------------------

 --
True
--
True
---------------------------------------------------------
![]()
![]() приращение
функции дифференциалом,
найти
приближённое
значение
выражения:
приращение
функции дифференциалом,
найти
приближённое
значение
выражения:

![]()
---------------------------------------------------------

1 -- True
---------------------------------------------------------
![]()
2 -- True
---------------------------------------------------------
![]()
![]() --
True
--
True
---------------------------------------------------------

0 -- True
---------------------------------------------------------
Заменив
в
точке
![]() приращение
функции
приращение
функции
![]() дифференциалом,
найти
приближённое
значение
выражения:
дифференциалом,
найти
приближённое
значение
выражения:
![]()
–0,03 -- True


---------------------------------------------------------
Найти
асимптоты
функции

![]()
---------------------------------------------------------
Найти
производную
![]() от
следующей
параметрически
заданной
функции:
от
следующей
параметрически
заданной
функции:

![]()
---------------------------------------------------------
 С
помощью
таблицы
и
правил
дифференцирования
арифметических
операций
найти
производную
следующей
функции:
С
помощью
таблицы
и
правил
дифференцирования
арифметических
операций
найти
производную
следующей
функции:
-- True
---------------------------------------------------------

3 -- True
---------------------------------------------------------
Найти
производное
![]() от
следующей
неявной
функции:
от
следующей
неявной
функции:
 --
True
--
True
---------------------------------------------------------
 С
помощью
правила
дифференцирования
сложной
функции
найти
производную
следующей
функции:
С
помощью
правила
дифференцирования
сложной
функции
найти
производную
следующей
функции:
-- True
![]()
![]()
---------------------------------------------------------
Вычислить неопределенный интеграл

![]() --
True
--
True
---------------------------------------------------------
Найти
производное
![]() от
следующей
неявной
функции:
от
следующей
неявной
функции:
 --
True
--
True

 --
True
--
True
--------------------------------------------------------- Вычислить неопределенный интеграл

![]()
---------------------------------------------------------
Найти
производное
![]() от
следующей
неявной
функции:
от
следующей
неявной
функции:
 --
True
--
True
---------------------------------------------------------

1 -- True
 ---------------------------------------------------------
Вычислить
определенный
интеграл
---------------------------------------------------------
Вычислить
определенный
интеграл
-- True
![]()

---------------------------------------------------------
Вычислить неопределенный интеграл


---------------------------------------------------------
Вычислить неопределенный интеграл
![]()
![]()
---------------------------------------------------------

– ∞ -- True
 ---------------------------------------------------------
Вычислить
определенный
интеграл
---------------------------------------------------------
Вычислить
определенный
интеграл
-- True
---------------------------------------------------------
Вычислить приближенно ln1,05.
0,05 -- True

![]()
---------------------------------------------------------


![]()

![]()
![]()
---------------------------------------------------------
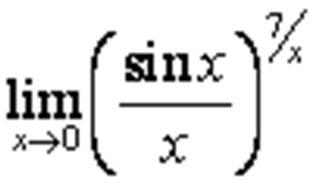
1 -- True
---------------------------------------------------------
Число 12 разложить на два положительных множителя так, чтобы их сумма была наименьшей.
![]()
---------------------------------------------------------
![]()
![]()
---------------------------------------------------------
![]()
![]()
![]()
---------------------------------------------------------
Дифференциал
![]() разности
двух
функций
разности
двух
функций
![]() и
и
![]() равен:
равен:
![]() --
True
--
True



 --
True
--
True
---------------------------------------------------------
![]()
![]() от
следующей
неявной
функции:
от
следующей
неявной
функции:
 --
True
--
True
---------------------------------------------------------
Найти
производное
![]() от
следующей
неявной
функции:
от
следующей
неявной
функции:
![]()

---------------------------------------------------------
Найти
интервалы
возрастания
функции

![]() --
True
--
True

![]()
---------------------------------------------------------

0 -- True
---------------------------------------------------------
Найти
коэффициент
многочлена
Тейлора
![]() для
функции
для
функции
![]() при
при
![]()
1 - True
---------------------------------------------------------

х = 2 -- True
--------------------------------------------------------
Написать
многочлен
Тейлора
2-го
порядка
для
функции
![]() при
при
![]()
![]()
---------------------------------------------------------
Заменив
в
точке
![]() приращение
функции
приращение
функции
![]() дифференциалом,
найти
приближённое
значение
выражения:
дифференциалом,
найти
приближённое
значение
выражения:
![]()
![]()
---------------------------------------------------------
Найти
производную
![]() от
следующей
параметрически
заданной
функции:
от
следующей
параметрически
заданной
функции:

![]()
---------------------------------------------------------
![]()
e -- True
![]()
![]()
---------------------------------------------------------
![]()
![]() при
при
![]()
---------------------------------------------------------
![]()
![]() на
приращении
аргумента
на
приращении
аргумента
![]()

0,4 -- True


---------------------------------------------------------
С помощью таблицы и правил дифференцирования арифметических операций найти производную следующей функции:
![]()
![]()
---------------------------------------------------------
![]()
![]()

![]()

 --
True
--
True
---------------------------------------------------------

1 -- True
---------------------------------------------------------
Вычислить неопределенный интеграл
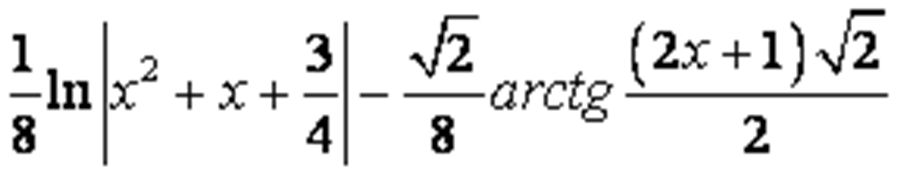

---------------------------------------------------------
-- True
![]()
![]()

![]()
---------------------------------------------------------
Найти
производное
![]() от
следующей
неявной
функции:
от
следующей
неявной
функции:
![]()

---------------------------------------------------------
Вычислить неопределенный интеграл
![]()
 --
True
--
True
---------------------------------------------------------
 --
True
--
True

![]()


---------------------------------------------------------
Найти
точку
максимума
функции

1 -- True
---------------------------------------------------------
![]()

![]()

---------------------------------------------------------
Написать
многочлен
Тейлора
1-
го
порядка
для
функции
![]() при
при
![]()
 --
True
--
True
---------------------------------------------------------
Найти
производные
второго
порядка
![]() от
следующих
функций:
от
следующих
функций:
![]()

---------------------------------------------------------
![]()
![]()
![]()
![]() --
True
--
True

![]() --
True
--
True
![]()
![]()
---------------------------------------------------------
![]()
![]() --
True
--
True
---------------------------------------------------------
 С
помощью
правила
дифференцирования
сложной
функции
найти
производную
следующей
функции:
С
помощью
правила
дифференцирования
сложной
функции
найти
производную
следующей
функции:
-- True.
---------------------------------------------------------
Вычислить определенный интеграл
 --
True
--
True
 ---------------------------------------------------------
Вычислить
определенный
интеграл
---------------------------------------------------------
Вычислить
определенный
интеграл
-- True
 ---------------------------------------------------------
Вычислить
неопределенный
интеграл
---------------------------------------------------------
Вычислить
неопределенный
интеграл
-- True
 ---------------------------------------------------------
Вычислить
определенный
интеграл
---------------------------------------------------------
Вычислить
определенный
интеграл
-- True
---------------------------------------------------------
Заменив
в
точке
![]() приращение
функции
приращение
функции
![]() дифференциалом,
найти
приближённое
значение
выражения:
дифференциалом,
найти
приближённое
значение
выражения:
![]()
1,98 -- True
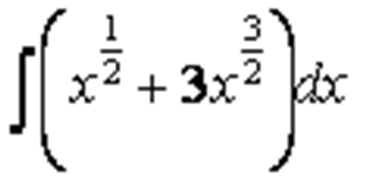

 ---------------------------------------------------------
Вычислить
определенный
интеграл
---------------------------------------------------------
Вычислить
определенный
интеграл
-- True.

![]() --
True
--
True
---------------------------------------------------------
 Применяя
логарифмическое
дифференцирование,
найти
производную
следующей
функции:
Применяя
логарифмическое
дифференцирование,
найти
производную
следующей
функции:
-- True

![]() --
True
--
True
---------------------------------------------------------
Найти
производные
второго
порядка
![]() от
следующих
функций:
от
следующих
функций:

-- True
---------------------------------------------------------
Написать
многочлен
Тейлора
2-
й
степени
для
функции
![]() при
при
![]()
![]()
---------------------------------------------------------
Найти
производные
второго
порядка
![]() от
следующих
функций:
от
следующих
функций:
![]()
![]()

![]() --
True
--
True
---------------------------------------------------------
Найти
интервалы
возрастания
функции
![]()
(2, ∞) -- True
![]()

---------------------------------------------------------
 С
помощью
таблицы
и
правил
дифференцирования
арифметических
операций
найти
производную
следующей
функции:
С
помощью
таблицы
и
правил
дифференцирования
арифметических
операций
найти
производную
следующей
функции:
-- True
---------------------------------------------------------
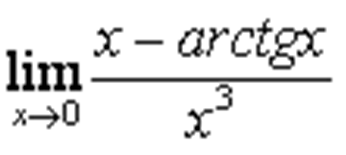
![]() --
True
--
True
---------------------------------------------------------
Найти
производную
![]() от
следующей
параметрически
заданной
функции:
от
следующей
параметрически
заданной
функции:

![]()
---------------------------------------------------------

![]()
---------------------------------------------------------
Найти
дифференциал
![]() от
следующей
функции:
от
следующей
функции:
![]()


![]() --
True
--
True

![]() --
True
--
True
---------------------------------------------------------
Найти
производное
![]() от
следующей
неявной
функции:
от
следующей
неявной
функции:
![]()
 --
True
--
True
![]()


![]() --
True
--
True
---------------------------------------------------------
Найти
дифференциал
![]() от
следующей
функции:
от
следующей
функции:
 --
True
--
True
![]()
![]()


---------------------------------------------------------
Вычислить определенный интеграл


 ---------------------------------------------------------
Вычислить
неопределенный
интеграл
---------------------------------------------------------
Вычислить
неопределенный
интеграл
-- True
---------------------------------------------------------
![]()

![]()
---------------------------------------------------------
-- True
![]()

![]() --
True
--
True

 --
True
--
True
---------------------------------------------------------
Вычислить неопределенный интеграл
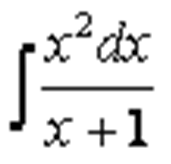

---------------------------------------------------------
![]()
![]() по
степеням ,
пользуясь
формулой
Тейлора.
по
степеням ,
пользуясь
формулой
Тейлора.
![]()
---------------------------------------------------------
Найти
промежутки
вогнутости
функции

![]()

![]() --
True
--
True
---------------------------------------------------------

![]()
---------------------------------------------------------

![]()

![]()


---------------------------------------------------------
![]()
![]() при
при
![]()
---------------------------------------------------------
![]()
![]()

---------------------------------------------------------
Найти
промежутки
выпуклости
функции

![]()

![]()
---------------------------------------------------------
![]()
 --
True
--
True

![]()
---------------------------------------------------------
![]()
![]() --
True
--
True

![]()
---------------------------------------------------------
![]()

---------------------------------------------------------

1 -- True
![]()
![]()
---------------------------------------------------------
![]()
![]()

![]() --
True
--
True

1 -- True

 --
True
--
True

![]()
---------------------------------------------------------


---------------------------------------------------------
Вычислить
приближенно
![]()
0,722 -- True
---------------------------------------------------------
Найти
производную
![]() от
следующей
параметрически
заданной
функции:
от
следующей
параметрически
заданной
функции:

![]()
---------------------------------------------------------
![]()
![]()
![]()

![]() --
True
--
True
---------------------------------------------------------

0 -- True

![]() --
True
--
True
![]()
![]()
![]()
![]() --
True
--
True
---------------------------------------------------------
Найти
наибольшее
значение
функции
![]() на
отрезке
[0,1].
на
отрезке
[0,1].
2 -- True
---------------------------------------------------------
Применяя логарифмическое дифференцирование, найти производную следующей
функции:
![]()
![]() --
True
--
True
---------------------------------------------------------

2 -- True
---------------------------------------------------------

![]()
---------------------------------------------------------
![]()
4 -- True

–1 -- True
---------------------------------------------------------
![]()
![]()
![]()
2,1 -- True
---------------------------------------------------------
![]()
![]() --
True
--
True
![]()
![]()
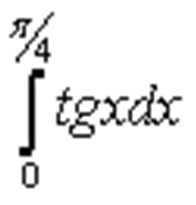
![]()
---------------------------------------------------------
![]()
0 -- True
---------------------------------------------------------
Вычислить определенный интеграл

![]() --
True
--
True
---------------------------------------------------------
Заменив
в
точке
![]() приращение
функции
приращение
функции
![]() дифференциалом,
найти
приближённое
значение
выражения:
дифференциалом,
найти
приближённое
значение
выражения:
![]()
1,01 -- True
---------------------------------------------------------

![]() --
True
--
True
---------------------------------------------------------
![]()
1 -- True
![]()
![]() --
True
--
True
---------------------------------------------------------
![]()
![]()
---------------------------------------------------------
![]()
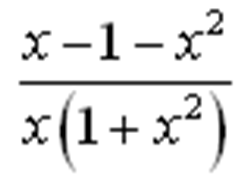 --
True
--
True

![]()
---------------------------------------------------------
![]()
![]()
![]()
---------------------------------------------------------
Найти
производную
![]() от
следующей
параметрически
заданной
функции:
от
следующей
параметрически
заданной
функции:

![]()
---------------------------------------------------------
![]()
![]() --
True
--
True

![]() --
True
--
True
![]()
 --
True
--
True


---------------------------------------------------------
![]()
![]()
---------------------------------------------------------
![]()
![]() при
при
![]()

![]()
---------------------------------------------------------
![]()
1 -- True
---------------------------------------------------------
-- True
![]()
![]()



![]()
![]()
![]()
---------------------------------------------------------

![]()
![]()

---------------------------------------------------------
Найти наибольшую площадь прямоугольника, вписанного в круг радиуса 3 см.
18 -- True
---------------------------------------------------------

0 -- True
---------------------------------------------------------
Найти
производное
![]() от
следующей
неявной
функции:
от
следующей
неявной
функции:
![]()
![]()
![]()
![]()
---------------------------------------------------------
Вычислить определенный интеграл

![]() --
True
--
True
![]()
 --
True
--
True

![]() --
True
--
True
---------------------------------------------------------
![]()
![]() в
точке
в
точке
![]() на
приращении
аргумента
на
приращении
аргумента
![]()
0,2 -- True
---------------------------------------------------------
![]()
0 -- True


---------------------------------------------------------
![]()
![]() разложить
по
степеням
двучлена .
разложить
по
степеням
двучлена .
![]()

![]() --
True
--
True
---------------------------------------------------------
![]()
1 -- True
---------------------------------------------------------
Найти
асимптоты
функции

![]()
---------------------------------------------------------
![]()
![]() --
True
--
True
---------------------------------------------------------
![]()
![]() от
следующих
функций:
от
следующих
функций:
![]() --
True
--
True
---------------------------------------------------------
![]()
![]() --
True
--
True
---------------------------------------------------------

4 -- True
---------------------------------------------------------
![]()
![]()



![]() --
True
--
True

![]() --
True
--
True
---------------------------------------------------------

![]()
---------------------------------------------------------

![]()
---------------------------------------------------------

–1 -- True
---------------------------------------------------------
Найти
точку
минимума
функции
![]()
![]() --
True
--
True

![]() --
True
--
True
---------------------------------------------------------
Заменив
в
точке
![]() приращение
функции
приращение
функции
![]() дифференциалом,
найти
приближённое
значение
выражения:
дифференциалом,
найти
приближённое
значение
выражения:
![]()
1,99 – True
---------------------------------------------------------
Найти
асимптоты
функции

 --
True
--
True
![]()
 --
True
--
True

 --
True
--
True
![]()

---------------------------------------------------------
Вычислить определенный интеграл

![]() --
True
--
True
![]()
![]() --
True
--
True

 --
True
--
True

1 -- True
---------------------------------------------------------
![]()
e -- True
---------------------------------------------------------
Найти
интервалы
возрастания
функции
![]()
![]()

![]()

![]()
---------------------------------------------------------
![]()
![]()

![]()
---------------------------------------------------------


![]()
 --
True
--
True
---------------------------------------------------------
![]()
1 -- True
---------------------------------------------------------
![]()
 --
True
--
True
---------------------------------------------------------


---------------------------------------------------------

1 -- True
---------------------------------------------------------
Найти
производное
![]() от
следующей
неявной
функции:
от
следующей
неявной
функции:
![]()


![]() --
True
--
True
---------------------------------------------------------
![]()
![]()
![]()

![]()
---------------------------------------------------------
Найти
точку
минимума
функции
![]()
0 -- True

![]() --
True
--
True
---------------------------------------------------------

3 -- True
---------------------------------------------------------
![]()

 --
True
--
True

 --
True
--
True

![]()
---------------------------------------------------------

![]() --
True
--
True
---------------------------------------------------------

1 -- True
---------------------------------------------------------
Заменив
в
точке
![]() приращение
функции
приращение
функции
![]() дифференциалом,
найти
приближённое
значение
выражения:
дифференциалом,
найти
приближённое
значение
выражения:
![]()
1,2 -- True
---------------------------------------------------------
![]()

---------------------------------------------------------

![]() --
True
--
True
---------------------------------------------------------
![]()
![]()
![]() --
True
--
True
---------------------------------------------------------

![]() --
True
--
True
---------------------------------------------------------

0 -- True
---------------------------------------------------------

![]()
---------------------------------------------------------

0 -- True
---------------------------------------------------------
Если
при
![]()
 то
функция имеет
в
точке
то
функция имеет
в
точке
![]() :
:
минимум -- True
---------------------------------------------------------

![]() при
при
![]()


---------------------------------------------------------
-- True
![]()
![]()
![]()
![]()
0,3 – True
---------------------------------------------------------
![]()
![]() на
отрезке
на
отрезке
![]() --
True
--
True
---------------------------------------------------------
![]()
1 -- True

![]()
---------------------------------------------------------
![]()
0 -- True
![]()
![]()
---------------------------------------------------------


---------------------------------------------------------
Найти
производную
![]() от
следующей
параметрически
заданной
функции:
от
следующей
параметрически
заданной
функции:

![]()
---------------------------------------------------------
![]()
5 -- True
---------------------------------------------------------
Найти
наименьшее
значение
функции
![]() на
отрезке
[-5,12].
на
отрезке
[-5,12].
5 -- True
---------------------------------------------------------
![]()
 --
True
--
True
---------------------------------------------------------
Найти
производные
второго
порядка
![]() от
следующих
функций:
от
следующих
функций:
![]()
 --
True
--
True
---------------------------------------------------------
 --
True
--
True
 ---------------------------------------------------------
Вычислить
неопределенный
интеграл
---------------------------------------------------------
Вычислить
неопределенный
интеграл
-- True
7.3.1. Если предел не существует, то это означает, что:
Варианты ответа:
#1) не имеет производной в точке x0;
