
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
Вариант 9
1. Вычислить пределы с помощью правила Лопиталя:
а)

![]()
![]() ;
б)
;
б)![]()
![]()
![]()
2. Провести
исследование и построить график функции:
![]() .
.
3. Построить график
функции в полярной системе координат
![]() .
.
4. Найти сторону
основания
![]() и боковое ребро
и боковое ребро![]() правильной шестиугольной
правильной шестиугольной
пирамиды, вписанной в сферу единичного радиуса и имеющей среди всех
таких пирамид
наибольшую боковую поверхность. Ответ:
 ,
,![]()
5. Вычислить
![]() функции
функции![]() .
Ответ:
.
Ответ:![]()
6. Вычислить с
помощью формулы Тейлора
![]() с
точностью до
с
точностью до
![]() .
Ответ:
.
Ответ:
![]()
7. Составить
уравнения касательной и нормали к кривой
 в точке
в точке
![]() и вычислить
и вычислить
![]() .
.
Ответ: Кас.
![]() ;
Норм:
;
Норм:![]() ,
,![]() .
.
8.
![]() .
Ответ:
.
Ответ:
 ,
,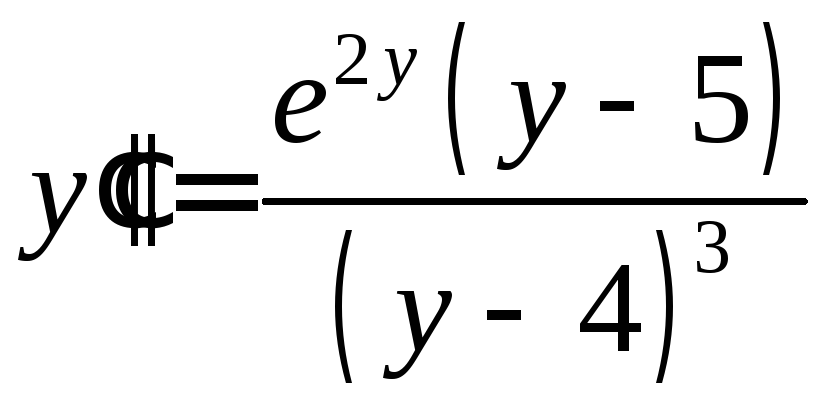 .
.
9. Вычислить предел
с помощью формулы Тейлора:

![]()
![]() .
.
10. Написать формулу
Лагранжа для функции
![]() и найти
и найти![]() на
на![]() .
.

11. По графику функции построить график ее первой производной
Вариант 10
1. Вычислить пределы с помощью правила Лопиталя:
а)

![]()
![]() ;
б)
;
б)![]()
![]()
![]()
2. Провести
исследование и построить график функции:
![]() .
.
3. Построить график
функции в полярной системе координат
![]()
![]() .
.
4. Найти сторону
основания
![]() и боковое ребро
и боковое ребро![]() правильной шестиугольной
правильной шестиугольной
пирамиды, вписанной в сферу единичного радиуса и имеющей среди всех
таких пирамид
наибольший объем. Ответ:
 ,
, .
.
5. Вычислить
![]() функции
функции .
Ответ:
.
Ответ:
6. Вычислить с
помощью формулы Тейлора
![]() с точностью до
с точностью до
![]() .
Ответ:
.
Ответ:
![]()
7. Составить
уравнения касательной и нормали к кривой
 в точке
в точке
![]() и вычислить
и вычислить
![]() .
.
Ответ: Кас.
![]() ;
Норм:
;
Норм:![]() ,
, .
.
8.
![]() .
Ответ:
.
Ответ:
 ,
, .
.
9. Вычислить предел
с помощью формулы Тейлора:

![]()
![]() .
.
10. Написать формулу
Коши для функций
![]() и
и![]() ,
и найти
,
и найти![]()
на
![]() .
.![]()
11. По графику функции построить график ее первой производной
Вариант 11
1. Вычислить пределы с помощью правила Лопиталя:
а)
![]()
![]()
![]() ;
б)
;
б)![]()
![]()
![]()
2. Провести
исследование и построить график функции:
![]() .
.
3. Построить график
функции в полярной системе координат
![]() .
.
4. На прямой
![]()
![]() ,
найти такую точку
,
найти такую точку![]() ,
чтобы сумма квадратов
,
чтобы сумма квадратов
расстояний от
неё до двух точек
![]() и
и![]() была наименьшей.
была наименьшей.
Ответ:
![]()
5. Вычислить
![]() функции
функции![]() .
Ответ:
.
Ответ:![]()
6. Вычислить с
помощью формулы Тейлора
![]() с точностью до
с точностью до
![]() .
.
Ответ:
![]()
7. Составить
уравнения касательной и нормали к кривой
 в
в
точке
![]() и вычислить
и вычислить![]() .
.
Ответ: Кас.
![]() ;
Норм:
;
Норм:![]() ,
,![]() .
.
8.
 .
Ответ:
.
Ответ:
 ,
, .
.
9. Вычислить предел
с помощью формулы Тейлора:

![]()
![]() .
.
10. Применима ли
теорема Ролля к функции
 на
на![]() ?
?
В каких точках
![]() ?
?
Теорема Ролля
применима.
![]()
![]()
![]() имеющее бесконечно много решений на
имеющее бесконечно много решений на![]() .
.
11. По графику функции построить график ее первой производной
Вариант 12
1. Вычислить пределы с помощью правила Лопиталя:
а)

![]()
![]() ;
б)
;
б)![]()
![]()
![]()
2. Провести
исследование и построить график функции:
 .
.
3. Построить график
функции в полярной системе координат
![]()
![]() .
.
4. Найти сторону
основания
![]() и боковое ребро
и боковое ребро![]() правильной треугольной
правильной треугольной
призмы, вписанной в сферу единичного радиуса и имеющей среди всех таких
призм наибольшую полную поверхность.
Ответ:
 ,
, .
.
5. Вычислить
![]() функции
функции![]() .
Ответ:
.
Ответ:![]()
6. Вычислить с
помощью формулы Тейлора
![]() с точностью до
с точностью до
![]() .
.
Ответ:
![]()
7. Составить
уравнения касательной и нормали к кривой
 в точке
в точке
![]() и вычислить
и вычислить
![]() .
.
Ответ: Кас.
![]() ;
Норм:
;
Норм:![]() ,
,![]() .
.
8.
![]() .Ответ:
.Ответ:
![]() ,
,![]() .
.
9. Вычислить предел
с помощью формулы Тейлора:

![]()
![]() .
.
10. Доказать, что
если
![]() является корнем многочлена
является корнем многочлена![]() кратности
кратности![]() ,
то для
,
то для
![]() он будет корнем
кратности
он будет корнем
кратности
![]() .
.
11. По графику функции построить график ее первой производной
