
- •Задачи контрольной работы по теоретической механике для студентов специальности тлдп(б) заочной формы обучения
- •1. Выбор задач и варианта
- •2. Правила оформления
- •3. Проверка и рецензирование контрольных работ
- •4. Задачи для контрольных работ
- •Задача с1
- •Задача с2
- •Кинематика Задача к1
- •Образец выполнения
- •Задача к2
- •Образец выполнения
- •Задача к3
- •Образец выполнения
- •Y1, y2
- •Задача д2
- •Задача д3
Образец выполнения
Условия задачи. Даны уравнения движения точки:
x=2cos(t⁄4) + 3,y= 2sin(t⁄8)1 (х,y– вcм ,t– в с ). (1)
Определить уравнение траектории точки; а также скорость, полное, касательное, нормальное ускорения точки и радиус кривизны ее траектории для момента времени t1= 1c.
Решение.Для получения уравнения траектории
точки исключим из уравнений движения
(1) времяt. Сначала
преобразуем уравнения (1) к виду![]() ,
,![]() .
.
Поскольку
tвходит в аргументы
тригонометрических функций причем один
аргумент вдвое больше другого, то,
воспользовавшись формулой![]() ,
получим :
,
получим :![]() .
.
Откуда после несложных преобразований находим уравнение траектории в виде
![]() (2)
(2)
Очевидно,
что это уравнение параболы с вершиной
В(1, –1). Как следует из уравнений
движения (1) точки, ее координаты изменяются
в пределах:![]() ;
;![]() .
Поэтому траекторией является лишь
участокАВСпараболы (рис. 4).
.
Поэтому траекторией является лишь
участокАВСпараболы (рис. 4).
Найдем
положение точки в момент времени
![]() с
. Для этого вычисляем значения координат:
с
. Для этого вычисляем значения координат:
![]() 1,59
см ,
1,59
см ,
![]() –
0,24 см
–
0,24 см
На рис.4 этому положению соответствует точка М.
Находим выражения для проекций вектора vскорости точки на координатные оси, используя известные формулы кинематики [1,c.102]:
![]() ,
,
![]()
(здесь и далее точки над переменными означают дифференцирование по времени) .
Находим модуль вектора скорости:
![]() .
.
Вычисляем
значения при
![]() с
:
с
:
![]() 1,11
см/c,
1,11
см/c,
![]() 0,73
см/c,
0,73
см/c,
![]() 1,33
см/с .
1,33
см/с .
Аналогично находим проекции вектора аускорения точки на координатные оси и модуль ускорения [1c.103]:
![]() ,
,
![]() ,
,
![]() .
.
Значения,
соответствующие
![]() с
будут:
с
будут:
![]() 0,87
см/c2,
0,87
см/c2,
![]() –
0,12 см/c2,
–
0,12 см/c2,
![]() 0,88
см/c2.
0,88
см/c2.
Величину
касательного ускорения точки найдем
как проекцию вектора ее ускорения
![]() на
направление вектора ее скоростиv
на
направление вектора ее скоростиv![]() ,
т.к. известно, что векторvнаправлен по касательной к траектории
:
,
т.к. известно, что векторvнаправлен по касательной к траектории
:
![]()
Здесь
![]() -
скалярное произведение вектороваиv.
-
скалярное произведение вектороваиv.
Для
момента времени
![]() с,
используя ранее найденные значения,
получим :
с,
используя ранее найденные значения,
получим :
![]() см/c2.
см/c2.
Поскольку
векторы касательного aи нормальногоanускорений взаимно перпендикулярны а
их сумма равна полному ускорению точки![]() ,
то можно найти величину нормального
ускорения, используя теорему Пифагора
(см. рис.7):
,
то можно найти величину нормального
ускорения, используя теорему Пифагора
(см. рис.7):![]() .
.
Для
момента времени
![]() получим
значение:
получим
значение:
![]() см/c2.
см/c2.
Радиус
кривизны траектории определяем, используя
известную формулу [1, c.109]
для нормального ускорения![]() (- радиус кривизны траектории точки).
(- радиус кривизны траектории точки).
Отсюда
получаем
![]() и вычисляем значение радиуса кривизны
в том месте траектории, где находится
точка в момент времени
и вычисляем значение радиуса кривизны
в том месте траектории, где находится
точка в момент времени![]() с
:
с
:![]() см
.
см
.
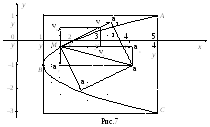
Ответ:![]() -уравнение
траектории;М(1,59; -0,24) - положение
точки;v(1,11; 0,73),v= 1,33 см/с - скорость;a(0,87;
-0,12),a= 0,88 см/с² -
ускорение;
= 3,85 см – радиус кривизны.
-уравнение
траектории;М(1,59; -0,24) - положение
точки;v(1,11; 0,73),v= 1,33 см/с - скорость;a(0,87;
-0,12),a= 0,88 см/с² -
ускорение;
= 3,85 см – радиус кривизны.
Задача к2
Плоский механизм состоит из жестких стержней 1–4и ползунаB, соединенных шарнирно; стержни1и4шарнирно связаны с неподвижными опорамиO1,O2(рис. К2.0 – К2.9). Положение механизма определяется углами,,,,, значения которых приведены в табл.5. Дуговые стрелки на рисунках указывают направление отсчета углов при построении чертежа. ТочкиDиKявляются серединами соответствующих звеньев. Длины стержней:l1= 0,4 м ,l2= 1,2 м ,l3= 1,4 м ,l4= 0,8 м.
В столбце "Скорости" табл.5 задана величина угловой скорости стержня 1или4, либо линейной скорости ползунаB. Вектор скоростиvBнаправлен от точкиBкb, а угловые скорости 1 , 4– против хода часовой стрелки.
Определить скорости двух точек механизма и угловую скорость стержня, указанные в столбце "Найти" таблицы 2
Таблица 2
|
Вариант |
Углы, град |
Скорости |
Найти | ||||||
|
|
|
|
|
|
1, с-1 |
4, с-1 |
vB, м/с | ||
|
0 |
30 |
150 |
120 |
0 |
60 |
2 |
– |
– |
vB, vE, 2 |
|
1 |
60 |
60 |
60 |
90 |
120 |
– |
3 |
– |
vA, vD, 3 |
|
2 |
0 |
120 |
120 |
0 |
60 |
– |
– |
10 |
vA, vE, 2 |
|
3 |
90 |
120 |
90 |
90 |
60 |
3 |
– |
– |
vB, vE, 2 |
|
4 |
0 |
150 |
30 |
0 |
60 |
– |
4 |
– |
vB, vA, 2 |
|
5 |
60 |
150 |
120 |
90 |
30 |
– |
– |
8 |
vA, vE, 3 |
|
6 |
30 |
120 |
30 |
0 |
60 |
5 |
– |
– |
vB, vE, 3 |
|
7 |
90 |
150 |
120 |
90 |
30 |
– |
5 |
– |
vA, vD, 3 |
|
8 |
0 |
60 |
30 |
0 |
120 |
– |
– |
6 |
vA, vE, 2 |
|
9 |
30 |
120 |
120 |
0 |
60 |
4 |
– |
– |
vB, vE, 3 |
|
Р |
Р | |
|
Р |
Р | |
|
Р |
Р | |
|
Р |
Р | |
|
Рис.
К2.8 |
Р | |
Указания.К2 – задача на использование методов кинематического анализа плоских механизмов. Расчет кинематических характеристик начинается с того звена механизма, движение которого задано в условии задачи. Затем расчет ведётся «по цепочке» с переходом от одного звена механизма к другому, связанному с ним. Для нахождения скоростей точек механизма и угловых скоростей его звеньев следует использовать теорему о проекциях скоростей двух точек твердого тела, а также свойства мгновенного центра скоростей.
Построение чертежа удобнее начать с того cтержня, положение которого определяется углом. Направляющие ползунаBдля большей наглядности рекомендуется изображать так, как показано на рис.8б.

 ис.
К2.0
ис.
К2.0 ис.
К2.1
ис.
К2.1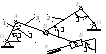 ис.
К2.2
ис.
К2.2 ис.
К2.3
ис.
К2.3 ис.
К2.4
ис.
К2.4 ис.
К2.5
ис.
К2.5 ис.
К2.6
ис.
К2.6 ис.
К2.7
ис.
К2.7
 ис.
К2.9
ис.
К2.9