Тут должен быть рисунок

Для этого заменим идеализированные пассивные элементы их операторными схемами замещения, ЭДС идеализированного источника напряжение Е- операторной ЭДС , мгновенные значения токов i(t) и напряжений U(t) ветвей- операторными токами I(p) и напряжениями U(p) соответственно.

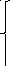Составим уравнение электрического равновесия цепи в операторной форме, используя метод контурных токов:

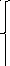
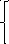
Решаем методом Крамера

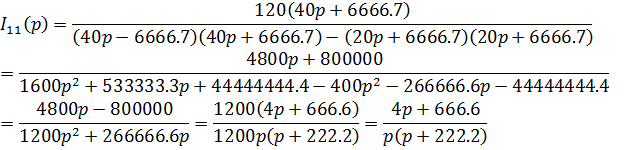
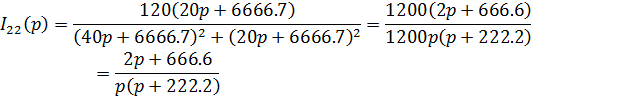
Тогда операторные изображения токов ветвей цепи:

Операторные изображения напряжений на резисторах к емкости можно записать на основании закона Ома в операторной форме:

Преобразуем полученные выражения к такому виду, при котором можно непосредственно воспользоваться таблицей обратного преобразования Лапласа:

Учитывая, что и , находим выражения для искомых тока и напряжений на элементах электрической цепи после замыкания ключа:

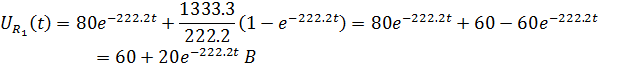
2.1 Анализ переходного процесса в цепи с двумя энергоемкими элементами операторным методом

Проведем анализ цепи до коммутации и определим независимые начальные условия: ток индуктивности и напряжение на емкости

Изобразим опреаторную схему замещения цепи после коммутации, для этого заменим идеализированные пассивные элементы их операторными схемами замещения, ЭДС идеализированного источника напряжения Е- операторной ЭДС , мгновенные значения токов i(t) и напряжений U(t) ветвей- их операторными токами I(p) и напряжениями U(p) соответственно.

Тут должен быть рисунок

Составим уравнение электрического равновесия цепи в операторной форме методом двух узлов:

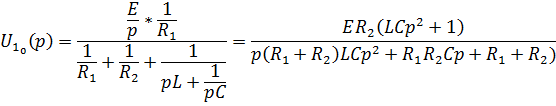
Определим операторный ток второй ветви:

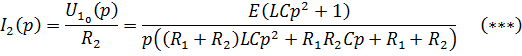
Изображение тока второй ветви можно записать в виде отклонения двух полиномов от р, не имеющих общих корней:

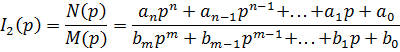
причем степень полинома M(p) выше, чем степень полинома N(p) и уравнение M(p)=0 не имеет кратных корней, то для перехода от изображения к оригиналу можно воспользоваться теоремой разложения:

где - корни уравнения

Поскольку знаменатель уравнение (***) имеет один корень равный нулю, т.е. , то для нахождения оригинала воспользуемся формулой теоремы разложения:

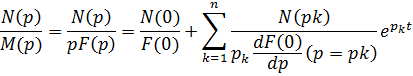
Подставим численные значения в уравнения:

Запишем:

N(p)=0.5*

F(p)=2*

и значение функции N(p) и F(p) при p=0:

N(0)=10 ; F(0)=40

Найдем корни уравнения

F(p)=2*

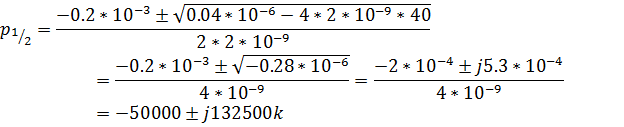
Вычислим производную и ее значения при u

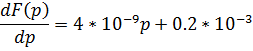
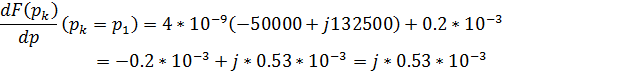
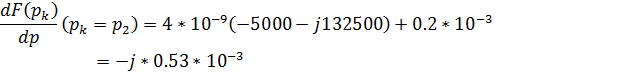
Определим N(p) при и :

N()

N()

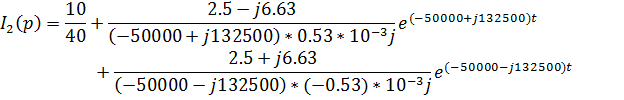
3.Расчет переходных процессов с помощью интеграла Дюамеля

Тут должен быть рисунок

R=1000 Oм

С=5000 мк Ф

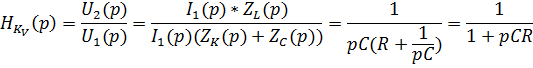
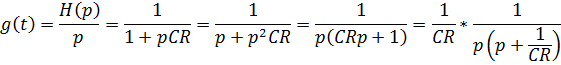
Тут должен быть рисунок

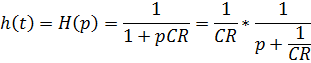
Искомая Лапласа

3.2. Определим реакцию цепи на воздействие прямоугольного импульса по ее переходной характеристики с помощью интеграла Дюамеля

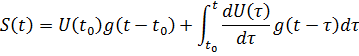
C помощью интеграла Дюамеля можно определить реакцию цепи на заданное воздействие, когда оно описывается кусочно-непрерывной функцией, т.е. функцией, которая имеет конечное число разрывов. В этом случае интервал интегрирования необходимо разбить на несколько промежутков в соответствии с интервалами непрерывности функции и учесть реакцию цепи на конечные скачки функции в точках разрыва.

Внешнее воздействие можно записать:

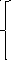0, приt0

U, при 0≤t≤

0, при t≥

При t0 реакция цепи непрерывна, поэтому реакция цепи определяется с помощью интеграла Дюамеля при

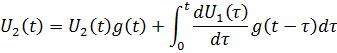
Выражение переходной характеристики цепи получим , заменим t на

Тогда реакция цепи на рассмотренном участке принимает вид:

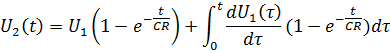
Поскольку U=const , , то реакция цепи

При t≥ интервал интегрирования содержит точку разрыва функции . Для определения реакции цепи интервал интегрирования разобьем на два промежутка [0;] и [] и учтем реакцию цепи на скачки функции в точке . Принимаем во внимание что при t≥. ,

Находим: