Классический метод анализа
Тут должна быть схема
C=150 мкФ
Искомый ток : 
Анализ цепи до
коммутации показывает, что 
Называемое
начальное условие определяется на
основании второго закона коммутации:
,
т.е. напряжение на емкости в первый
момент после коммутации равно напряжению
на емкости до коммутации, а затем может
плавно изменяться.
Д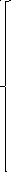
ля
нахождения тока
составим дифференциальное уравнение
цепи после коммутации.
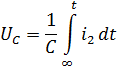
Последовательно
исключаем все неизвестные величины
кроме тока 
запишем выражение:
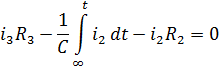
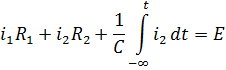
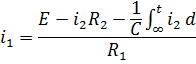
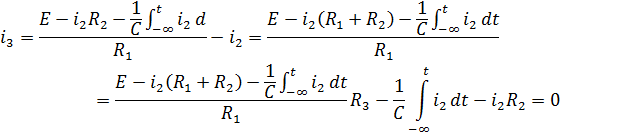
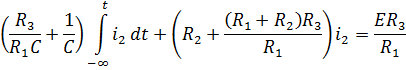
Чтобы избавиться от интегралов осуществим дифференцирование его по времени:
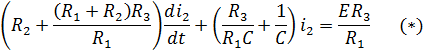
Решение уравнения
(*) будем искать в виде суммы свободной
и вынужденной 
составляющих тока второй ветви:
Анализ
установившегося процесса в цепи после
коммутации позволяет найти вынужденную
составляющую тока 
.
В установившемся режиме при постоянном токе сопротивление емкости равно бесконечности и схема принимает следующий вид:
тут должна быть схема
Вынужденный ток
Свободную
составляющую тока 
находим, решая однородное дифференциальное
уравнение , полученное из дифференциального
уравнения (*)(правая часть равно нулю)
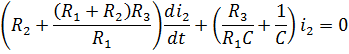
Далее составляем характеристическое уравнение цепи:
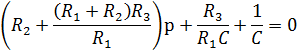
Находим его корень:
и составляем вид свободной составляющей тока второй ветви:
Общей вид реакции цепи составляющей сумме вынужденной и свободной составляющих тока второй ветви:
О
пределим
постоянную интегрирования А по зависимым
начальным условиям, т.е. по значения
тока
в начальный момент времени после
коммутации и уравнениям электрического
равновесия цепи при t=0:
т
.к.
то
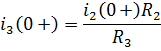
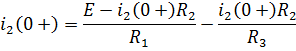
Тогда постоянная интегрирования равна:
2=
А=2
т.е. ток 
после замыкания ключа будет записан в
виде:
Определим напряжение на элементах цепи:
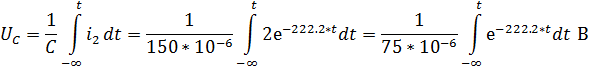
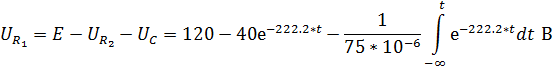
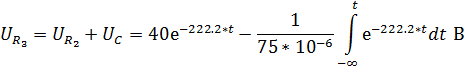
Cоставим характеристическое уравнение для цепи:
тут должна быть схема
Комплексное
входное сопротивление рассмотрим
относительно контактов ключа 
первой
ветви:
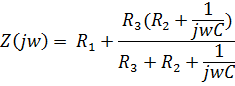
Заменим jw на p
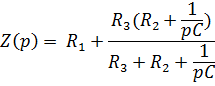
Получим операторное входное сопротивлние
Приравняем его к нулю:
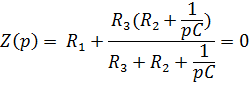
Найдем корень характеристического уравнения:
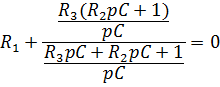
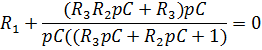
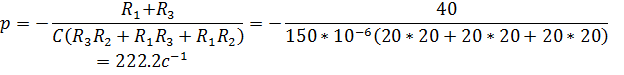
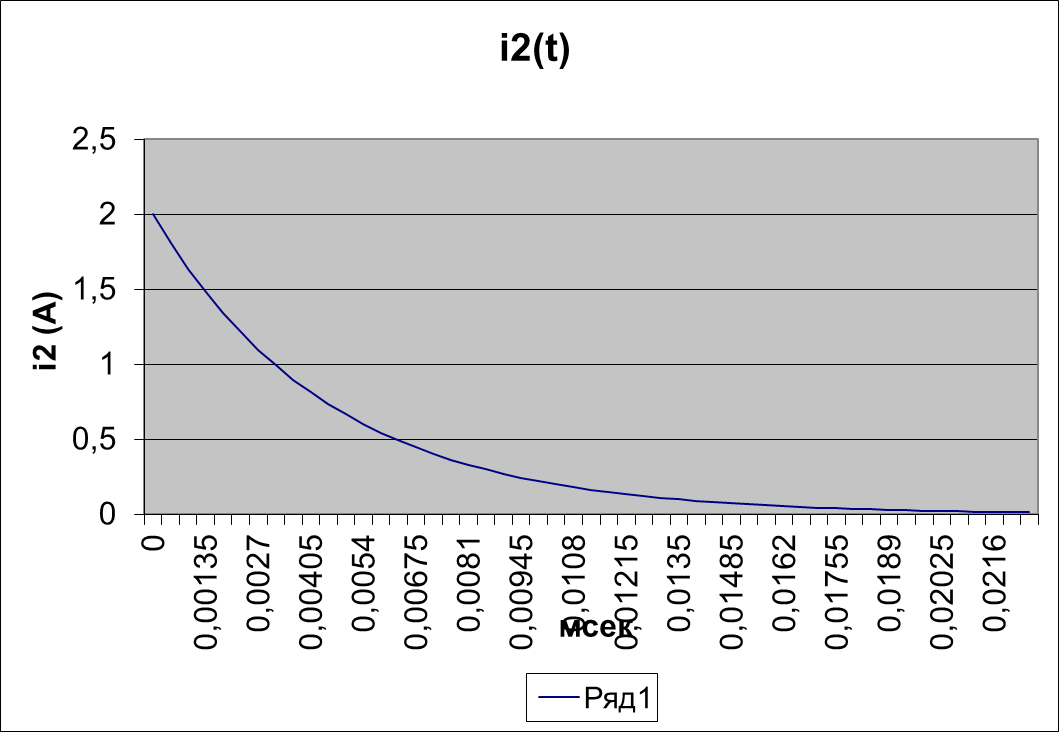
1.1.2.
Построить график
тока второй ветви 
цепи, рассмотренной в задании 1.1.1.
диапазон
изменения времени : от 0 до (13,5
22,5)
мс
|
|
Время |
i2(t) |
|
0 |
0 |
2 |
|
0,1 |
0,00045 |
1,809675 |
|
0,2 |
0,0009 |
1,637462 |
|
0,3 |
0,00135 |
1,481636 |
|
0,4 |
0,0018 |
1,34064 |
|
0,5 |
0,00225 |
1,213061 |
|
0,6 |
0,0027 |
1,097623 |
|
0,7 |
0,00315 |
0,993171 |
|
0,8 |
0,0036 |
0,898658 |
|
0,9 |
0,00405 |
0,813139 |
|
1 |
0,0045 |
0,735759 |
|
1,1 |
0,00495 |
0,665742 |
|
1,2 |
0,0054 |
0,602388 |
|
1,3 |
0,00585 |
0,545064 |
|
1,4 |
0,0063 |
0,493194 |
|
1,5 |
0,00675 |
0,44626 |
|
1,6 |
0,0072 |
0,403793 |
|
1,7 |
0,00765 |
0,365367 |
|
1,8 |
0,0081 |
0,330598 |
|
1,9 |
0,00855 |
0,299137 |
|
2 |
0,009 |
0,270671 |
|
2,1 |
0,00945 |
0,244913 |
|
2,2 |
0,0099 |
0,221606 |
|
2,3 |
0,01035 |
0,200518 |
|
2,4 |
0,0108 |
0,181436 |
|
2,5 |
0,01125 |
0,16417 |
|
2,6 |
0,0117 |
0,148547 |
|
2,7 |
0,01215 |
0,134411 |
|
2,8 |
0,0126 |
0,12162 |
|
2,9 |
0,01305 |
0,110046 |
|
3 |
0,0135 |
0,099574 |
|
3,1 |
0,01395 |
0,090098 |
|
3,2 |
0,0144 |
0,081524 |
|
3,3 |
0,01485 |
0,073766 |
|
3,4 |
0,0153 |
0,066747 |
|
3,5 |
0,01575 |
0,060395 |
|
3,6 |
0,0162 |
0,054647 |
|
3,7 |
0,01665 |
0,049447 |
|
3,8 |
0,0171 |
0,044742 |
|
3,9 |
0,01755 |
0,040484 |
|
4 |
0,018 |
0,036631 |
|
4,1 |
0,01845 |
0,033145 |
|
4,2 |
0,0189 |
0,029991 |
|
4,3 |
0,01935 |
0,027137 |
|
4,4 |
0,0198 |
0,024555 |
|
4,5 |
0,02025 |
0,022218 |
|
4,6 |
0,0207 |
0,020104 |
|
4,7 |
0,02115 |
0,018191 |
|
4,8 |
0,0216 |
0,016459 |
|
4,9 |
0,02205 |
0,014893 |
|
5 |
0,0225 |
0,013476 |
1.2.
Методика анализа п.п. классическим методом в цепи с двумя энергоемкими элементами