2.2. Задания к выполнению работы
1. На числовом примере доказать выражения
1.
;
2.
;
3.
.
2.
Проверить справедливость нижеследующих
равенств для множеств
;
;
и выяснить верны ли равенства для
произвольных
.
1.
;
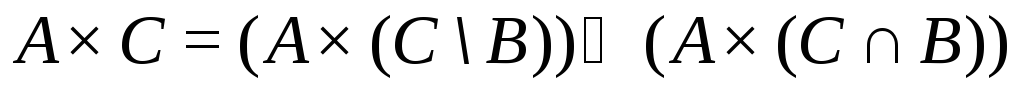2.
;
3.
;
4.
;
5.
;
6.
;
7.
;
8.
;
9.
.
10.
.
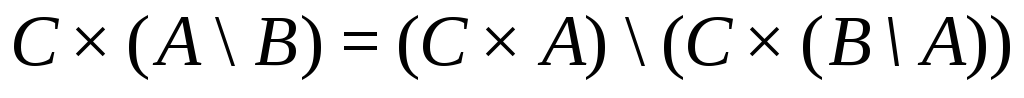Пример решения задания 2
Вариант 1
;
;
;
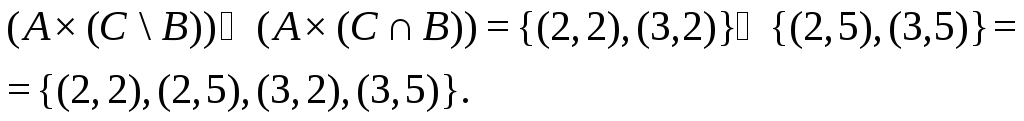
Как видим, равенство для заданных множеств выполняется.
Теперь проверим
это равенство для общего случая
(произвольных множеств
.
Пусть
,
,
,
где
,
,
,
–
списки элементов.
Тогда
,
где
–
множества пар элементов, первая компонента
которых входит в список
и
,
а вторая – в список
.
,
,
.
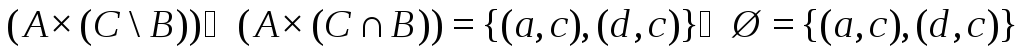Как видим множества
и
состоят
из пар одинакового вида
,
следовательно, равенство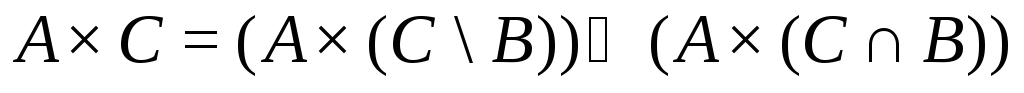
выполняется для произвольных множеств
.
3. Сравнить кортежи:
1. а)
и
;
б)
и
;
в)
и
;
2.
и
;
3.
и
;
4.
и
;
5.
и
Пример решения задания 3
Вариант 1
а) Кортежи
и
равны, так как
;
;
;
б) кортежи
и
различны, хотя имеют одинаковую длину
и одно и то же множествокоординат,
но эти координаты располагаются в разном
порядке; в) кортежи
и
различны, так как имеют разную длину.
4.
Дано соответствие
(табл.
2.1).
1. Изобразить
соответствие
в виде векторной диаграммы.
2. Выяснить, какими из 4 основных свойств (всюду определенность, сюръективность, функциональность, инъективность) обладает соответствие.
3. Найти образ
множества
и прообраз множества
при данном соответствии.
4. Построить
соответствие между бесконечными
множествами, обладающее тем же набором
свойств, что и
.
5. Построить соответствие между конечными множествами, обладающее набором свойств, противоположным данному.
Для данного и построенных соответствий отметить случаи отображений, указать их тип, отметить случаи биекций.
Пример решения задания 4
Вариант 30
1.
Изображаем соответствие
в
виде векторной диаграммы (рис. 2.6).
2. Определяем какими из 4 основных свойств обладает данное соответствие.
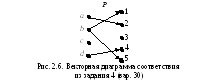
Таблица 2.1
Варианты задания 4
-
Вариант
1
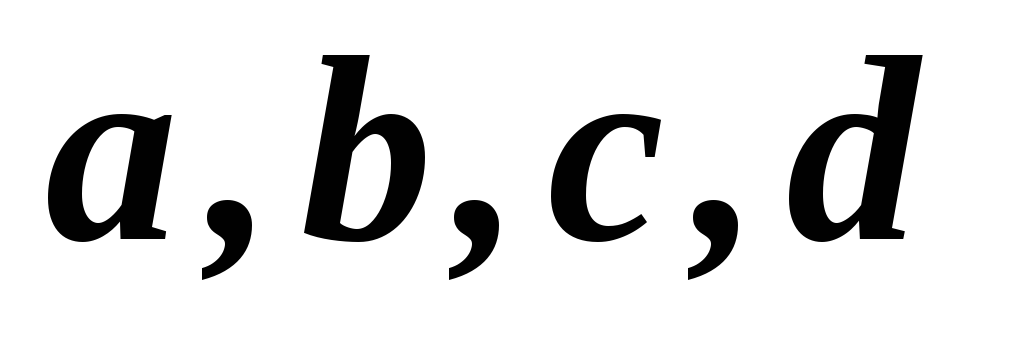
1,2,3,4,5
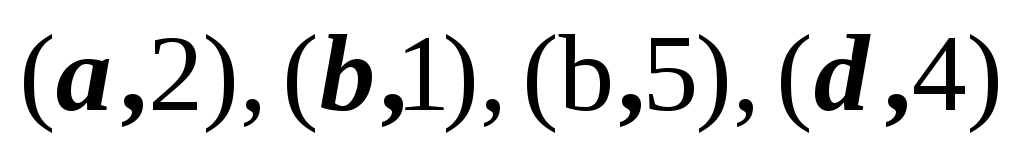
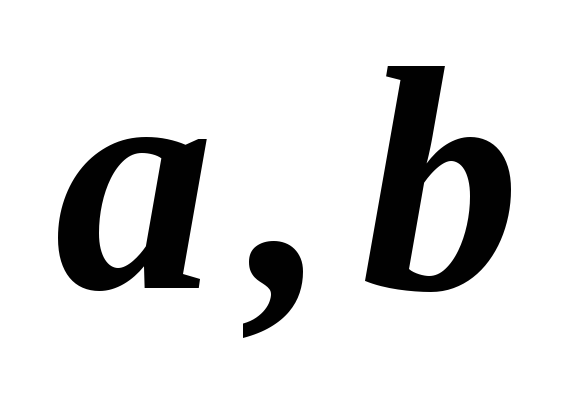
3,4
2
1,2,3
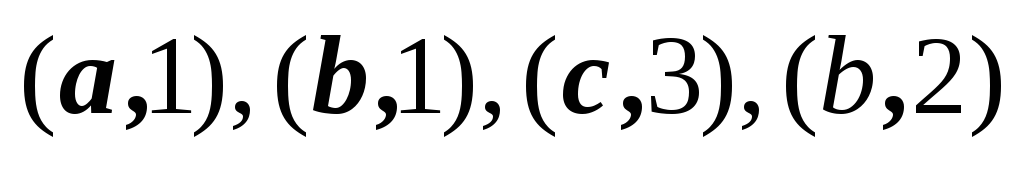
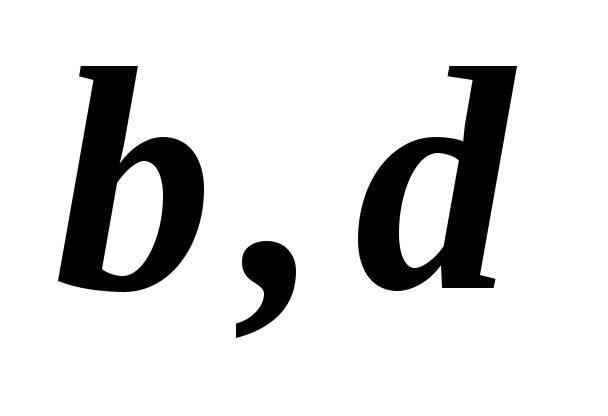
1,3
3
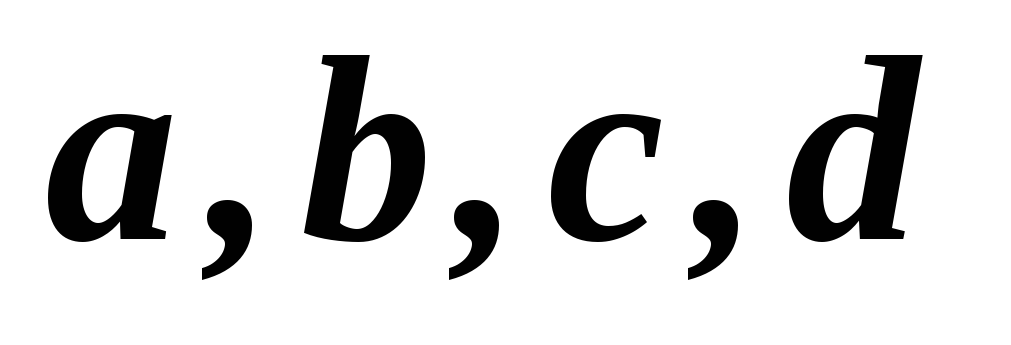
1,2,3,4
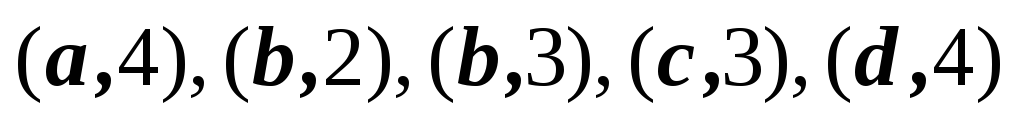
3,4
4
1,2,3,4,5
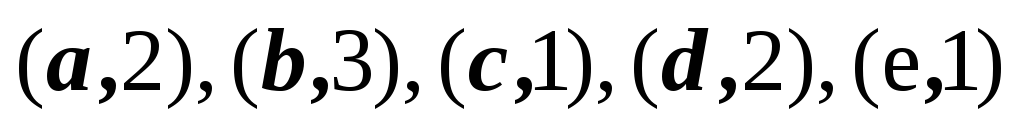
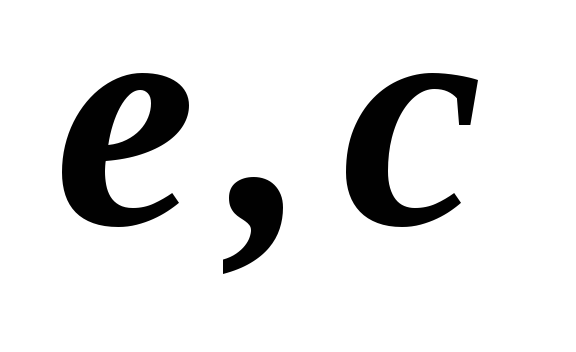
2,3
5
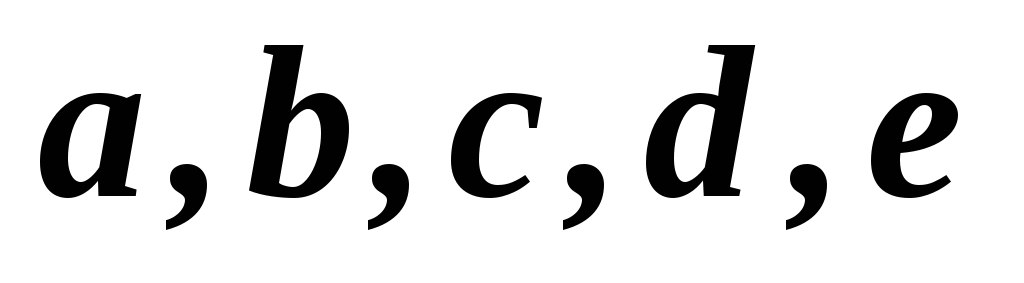
1,2,3,4,5
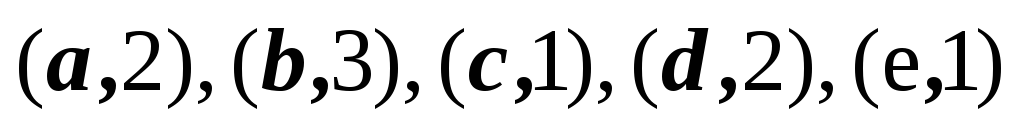
2,3
6
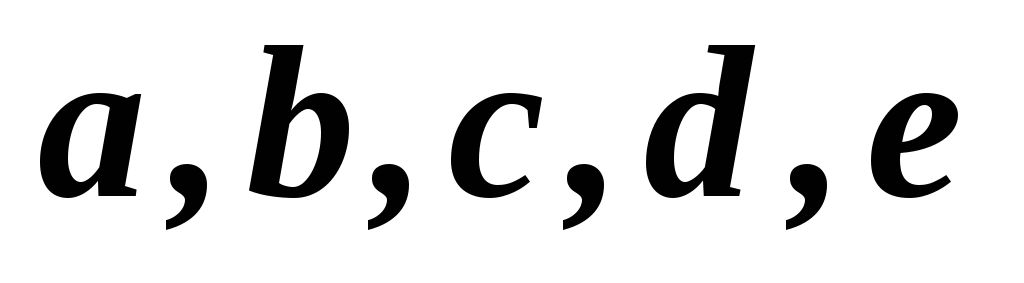
1,2,3,4,5
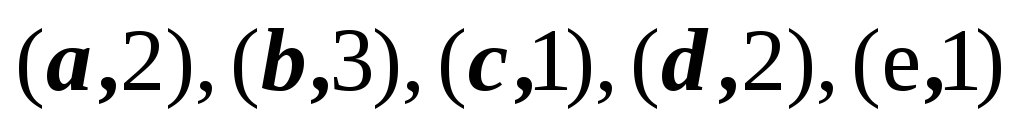
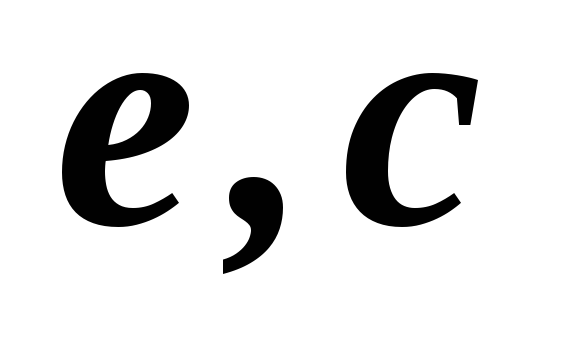
2,3
7
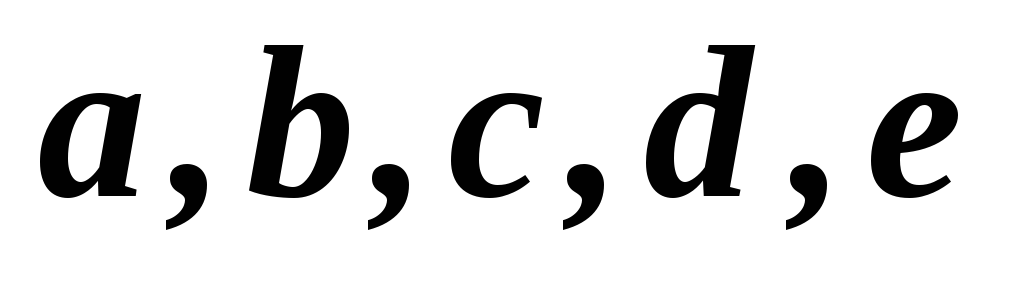
1,2,3,4,5
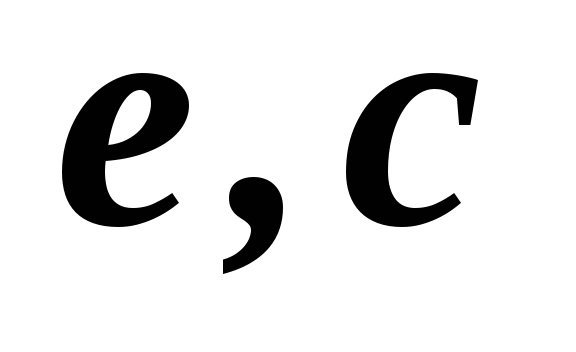
2,3
8
1,2,3,4,5
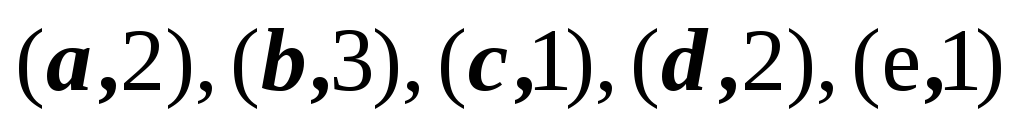
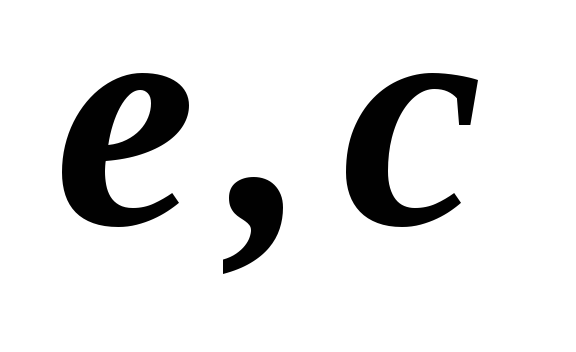
2,3
9
1,2,3,4,5
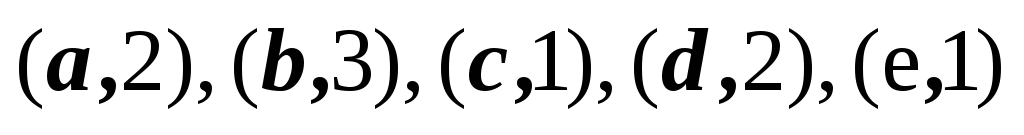
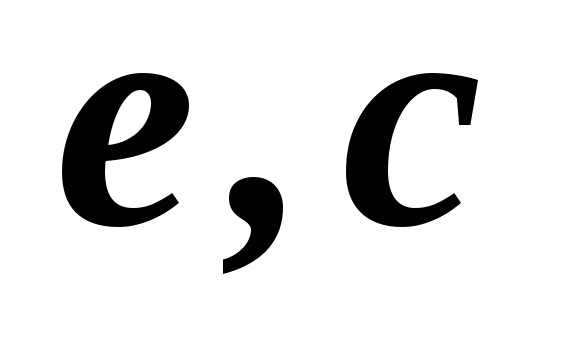
2,3
10
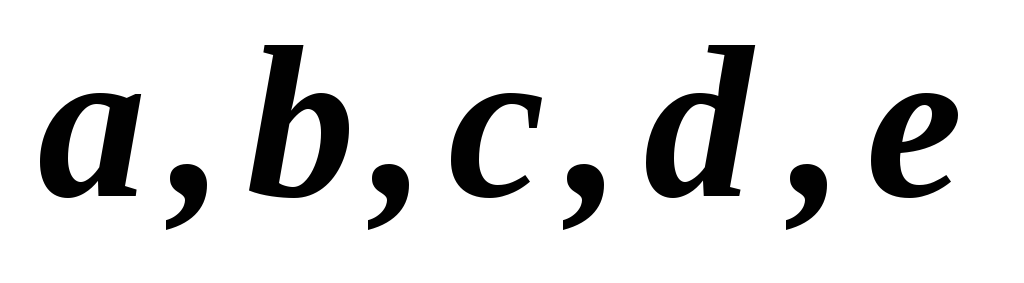
1,2,3,4,5
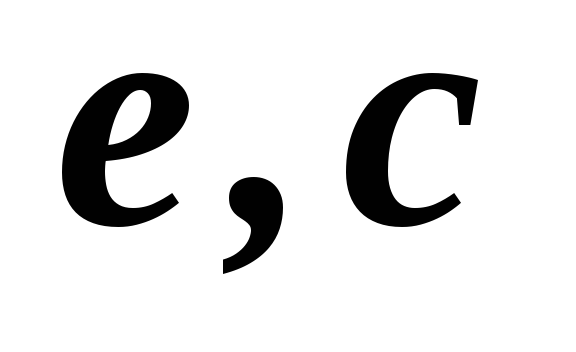
2,3
11
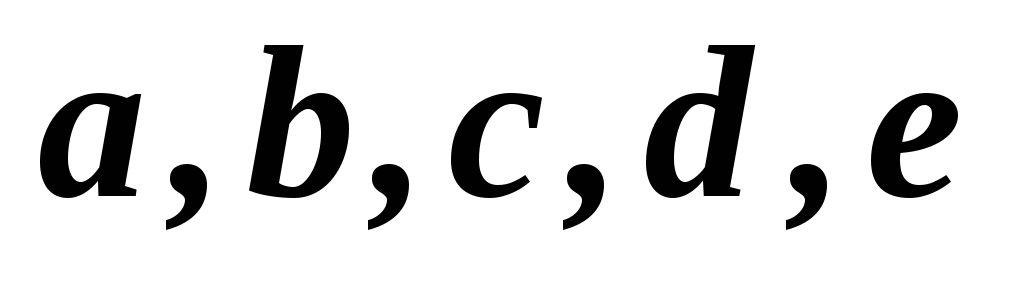
1,2,3,4,5
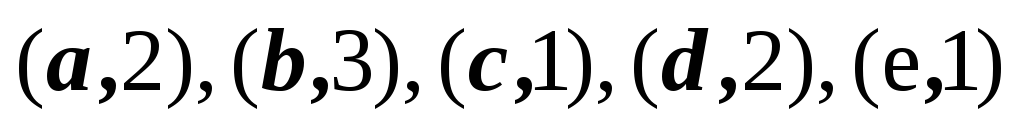
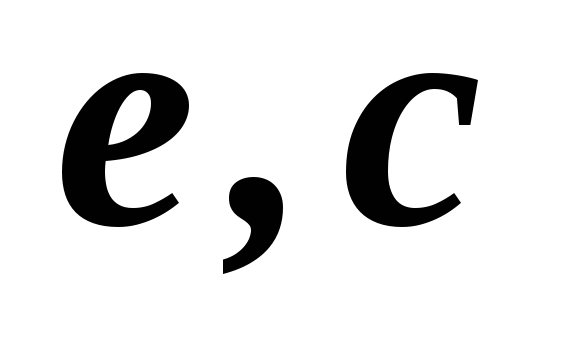
2,3
12
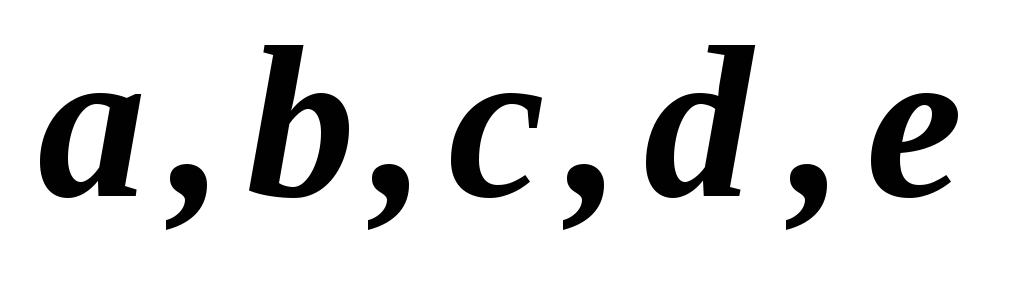
1,2,3,4,5
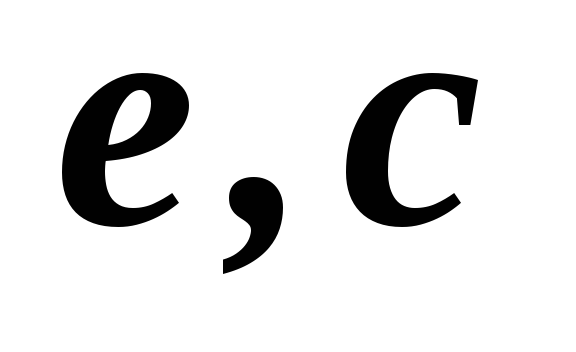
2,3
13
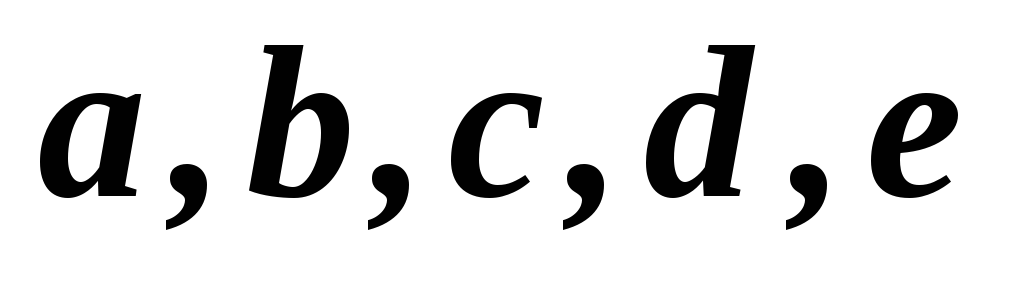
1,2,3,4,5
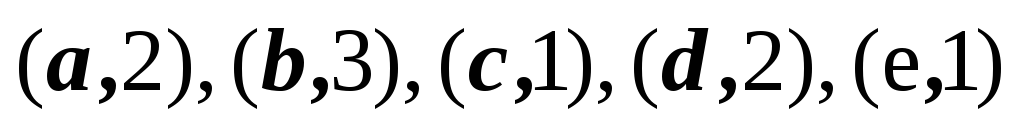
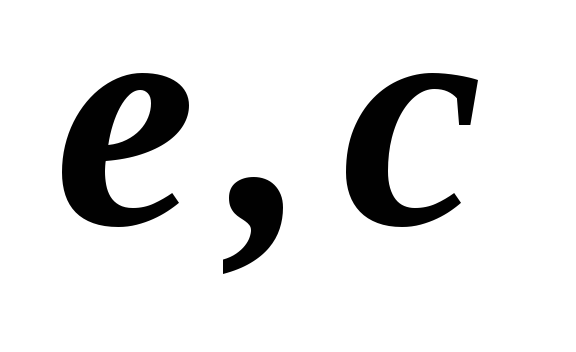
2,3
14
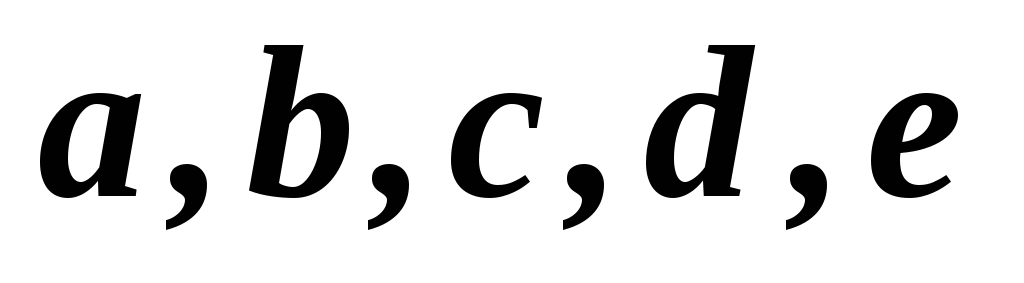
1,2,3,4,5
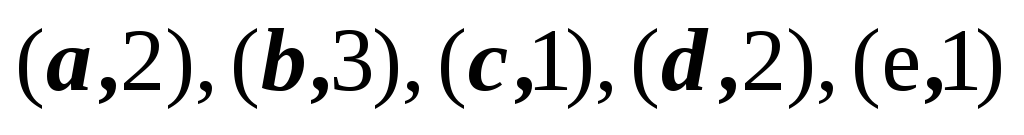
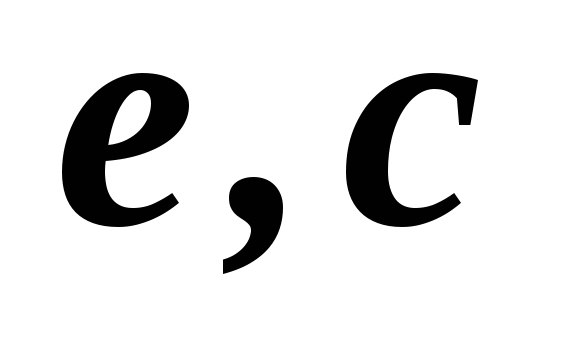
2,3
15
1,2,3,4,5
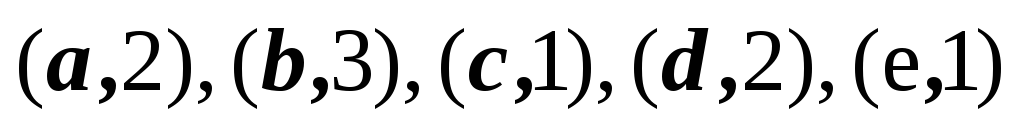
2,3
16
1,2,3,4,5
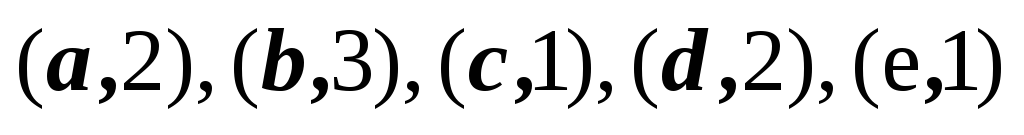
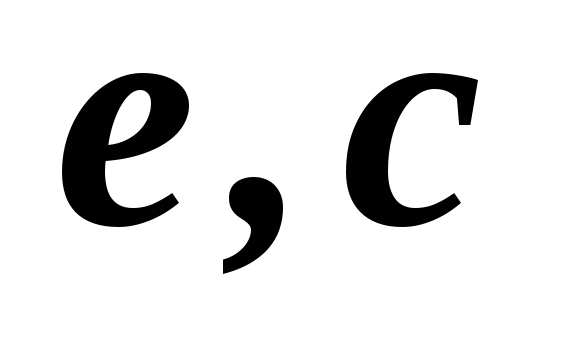
2,3
17
1,2,3,4,5
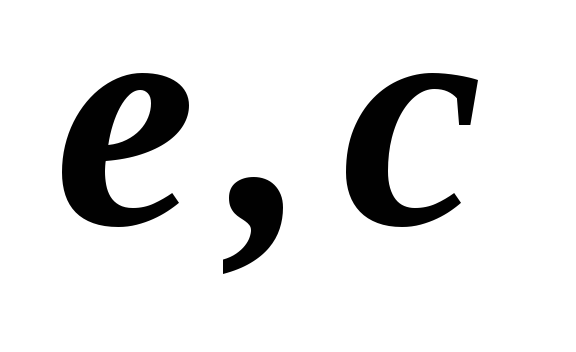
2,3
18
1,2,3,4,5
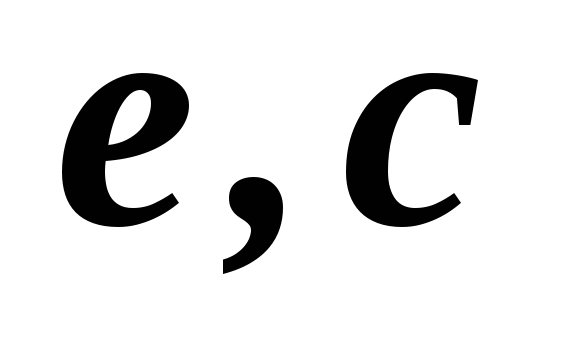
2,3
19
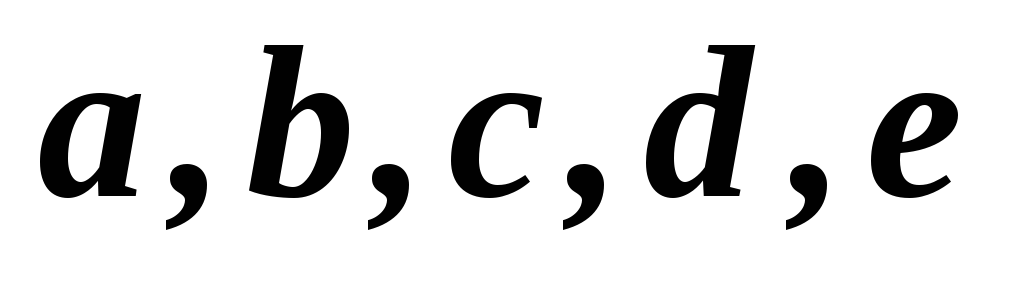
1,2,3,4,5
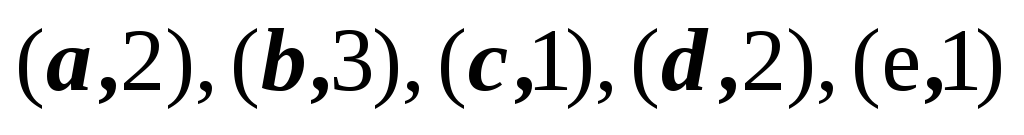
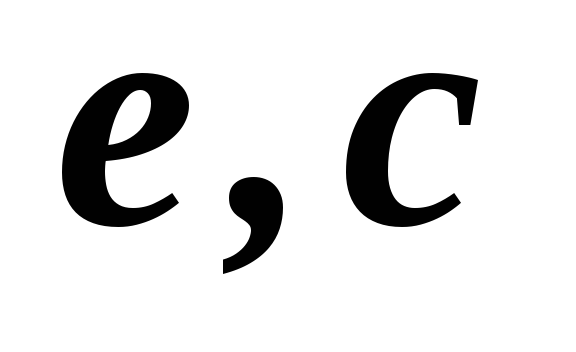
2,3
20
1,2,3,4,5
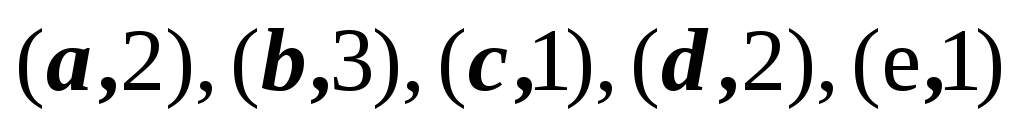
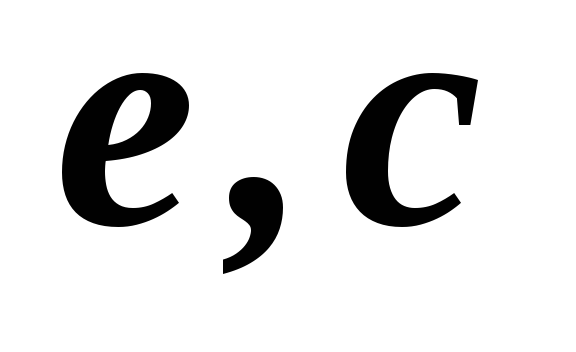
2,3
21
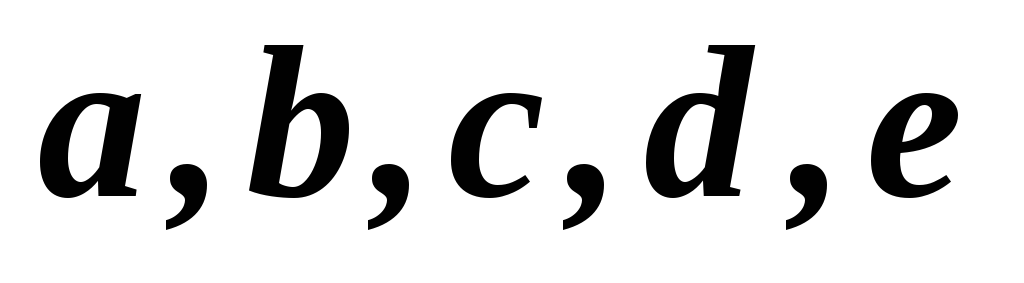
1,2,3,4,5
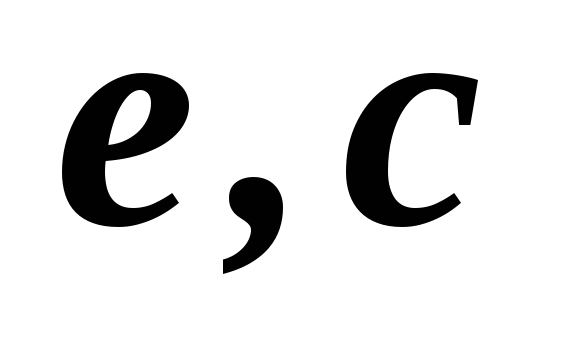
2,3
22
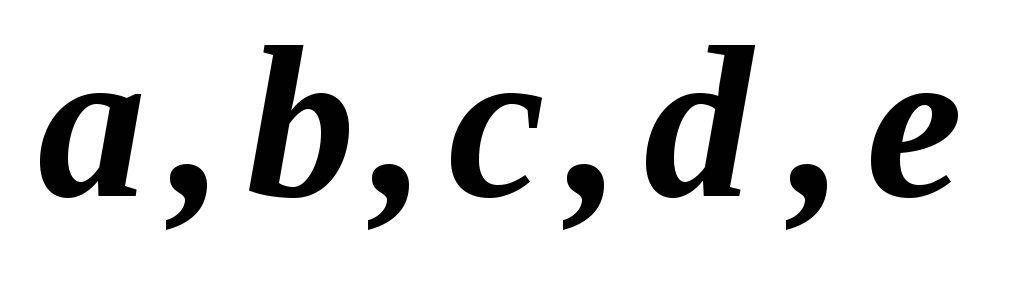
1,2,3,4,5
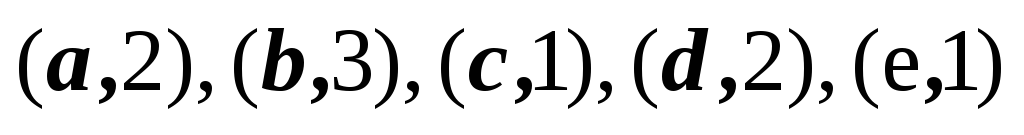
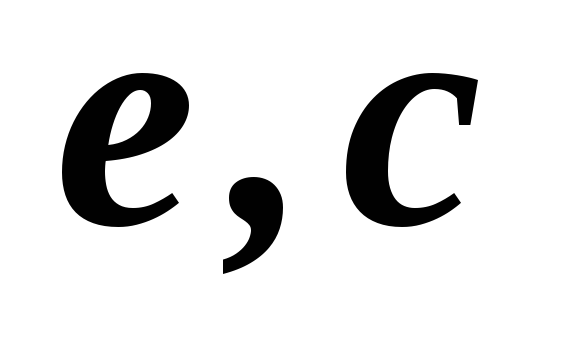
2,3
23
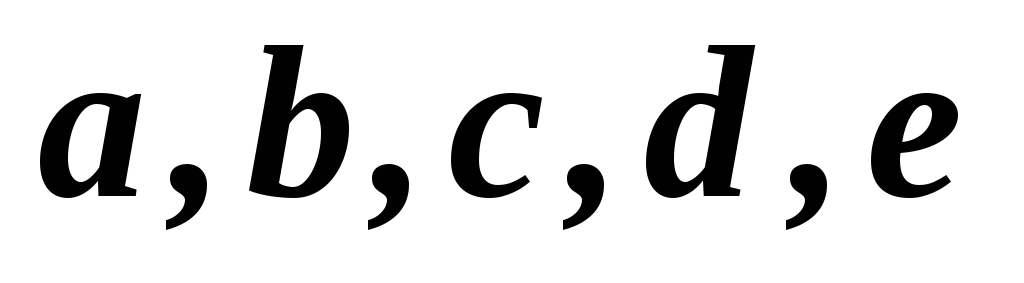
1,2,3,4,5
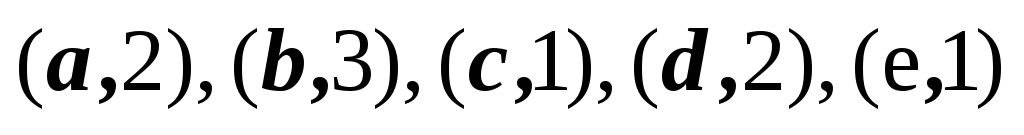
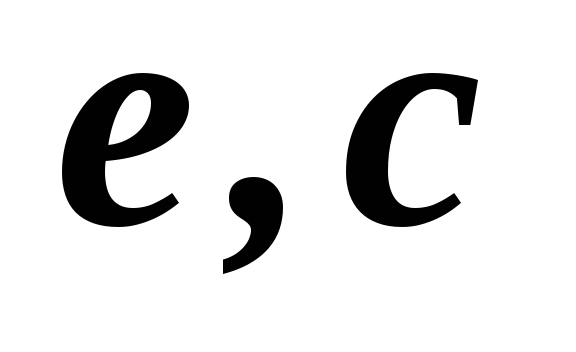
2,3
24
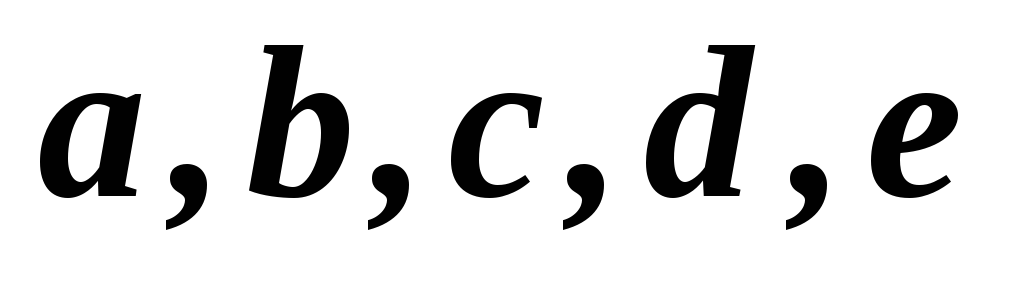
1,2,3,4,5
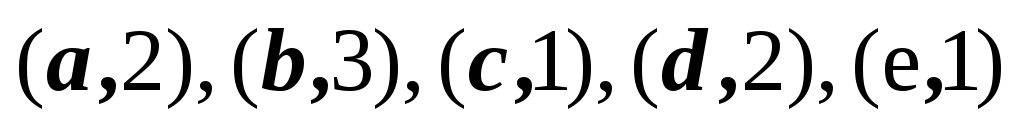
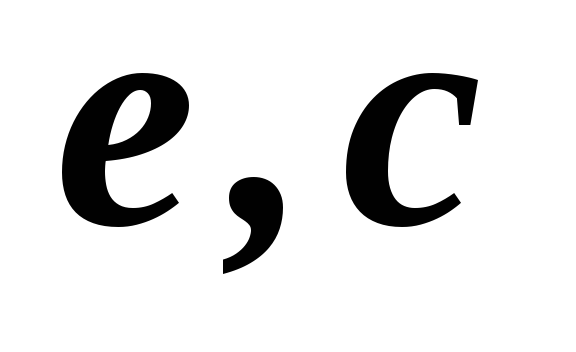
2,3
25
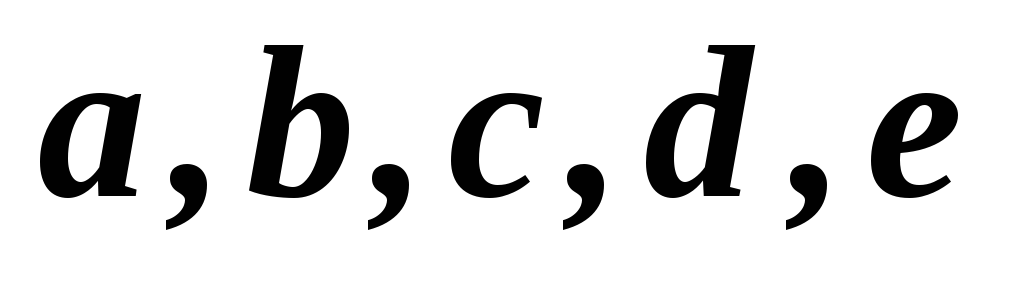
1,2,3,4,5
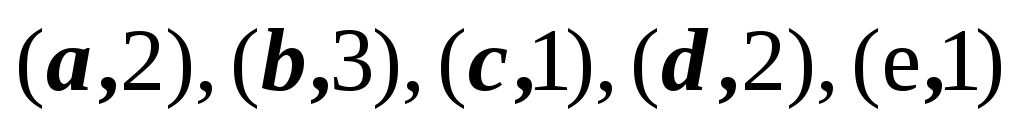
2,3
26
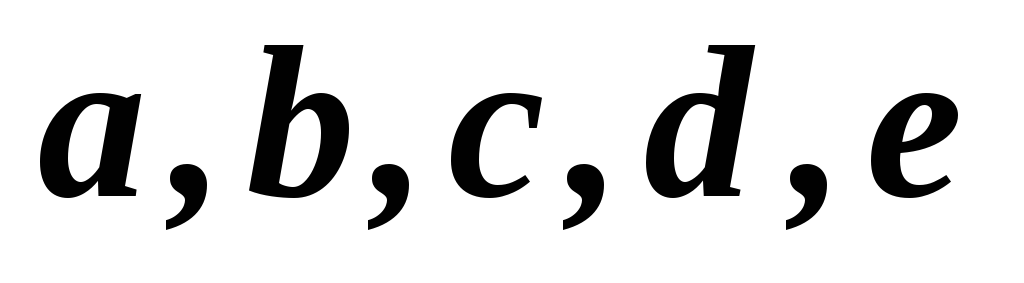
1,2,3,4,5
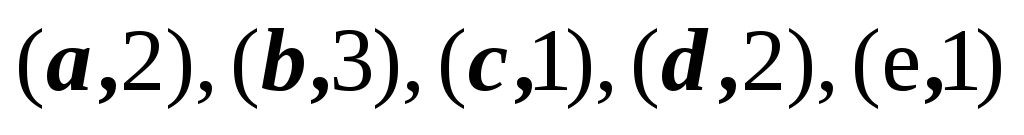
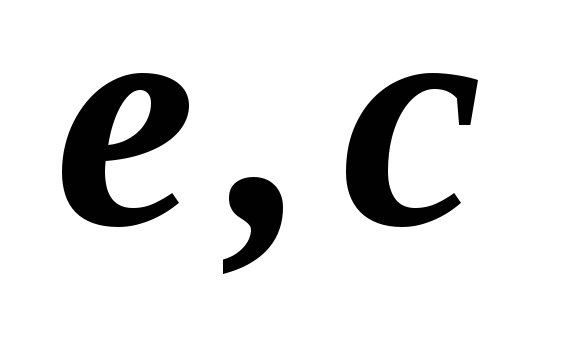
2,3
27
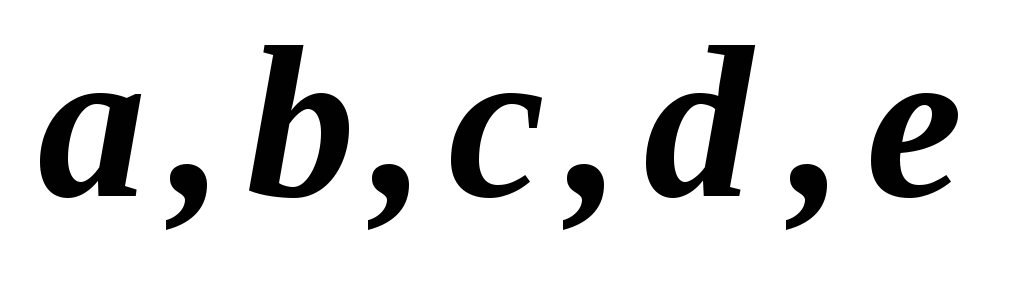
1,2,3,4,5
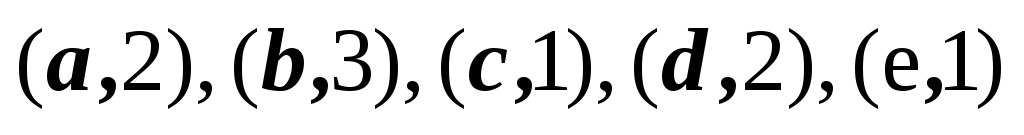
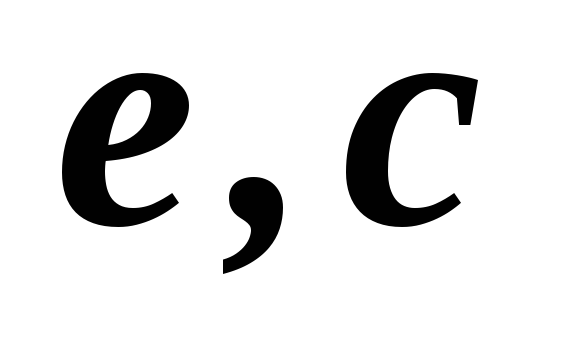
2,3
28
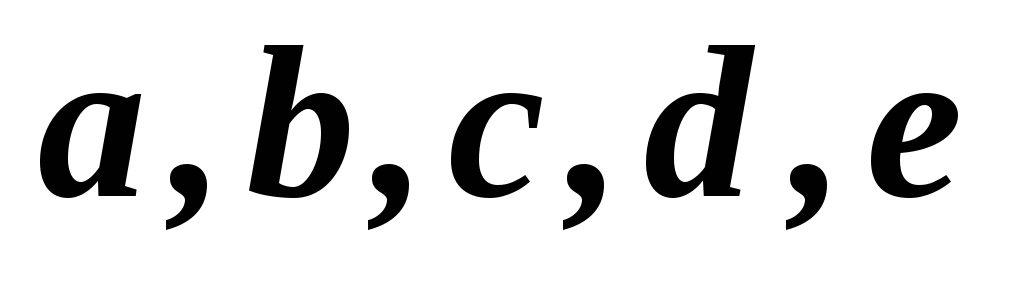
1,2,3,4,5
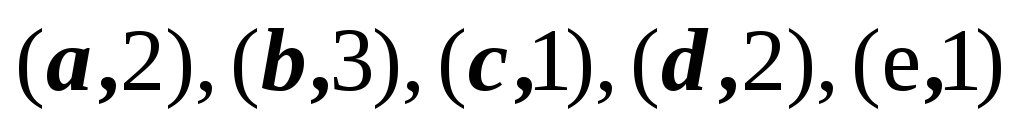
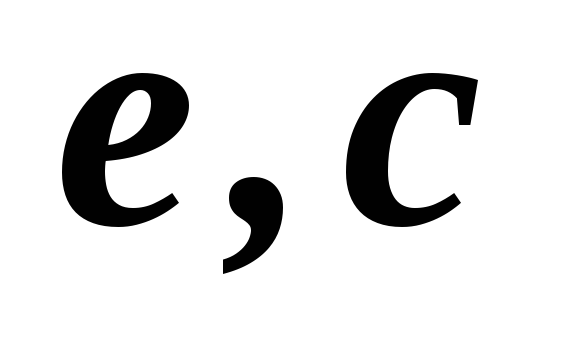
2,3
29
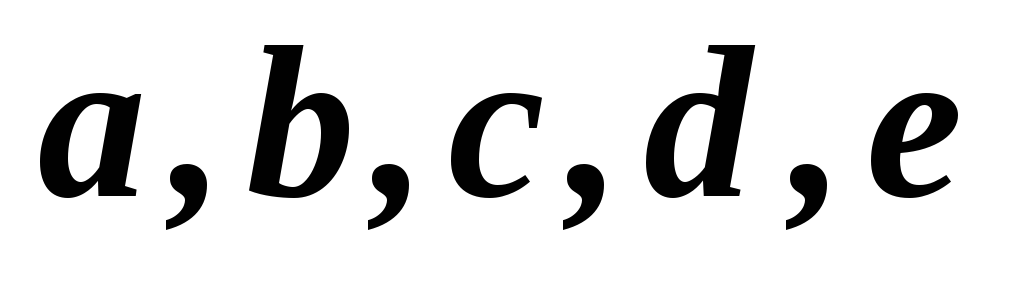
1,2,3,4,5
2,3
30
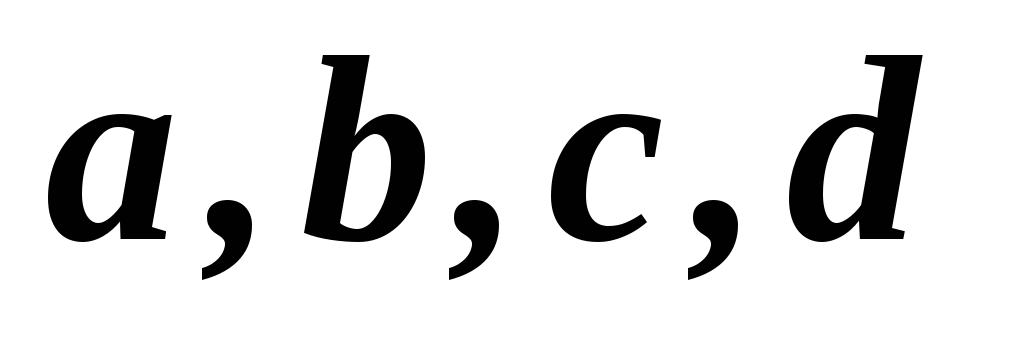
1,2,3,4,5
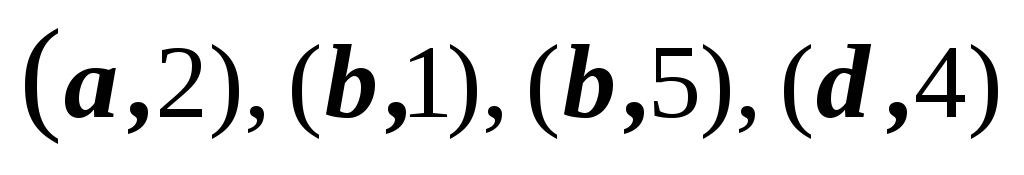
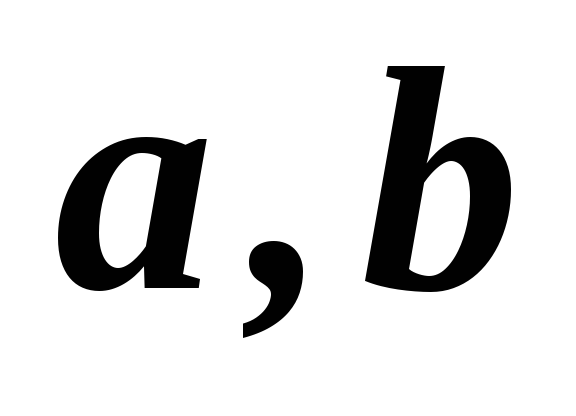
3,4
а)
всюду
определенность:
для этого необходимо выполнение равенства
.
В примере соответствие
,
откуда следует, что проекция соответствия
на первую ось равна
(первые
компоненты соответствия
).
При
этом исходное множество
в соответствии
равно
,следовательно
.
Таким
образом, соответствие не
всюду определено.
б) сюръективность:
для этого необходимо выполнение равенства
.
В примере
.
Соответствие не
сюръективно.
в) функциональность:
для этого необходимо чтобы образом
любого элемента из
множества
являлся единственный элемент из
множества
.
Сравнивая множества
и
,
видим, что одинаковым первым элементам
(координатам)
из множества
соответствует не единственный элемент
из множества
:
элементы 1 и 5
(соответствие
содержит две пары
и
с одинаковыми
первыми и различными вторыми координатами).
Следовательно, соответствие
не
функционально.
г) инъективность:
для этого необходимо чтобы прообразом
любого элемента из
множества
являлся единственный элемент из
множества
(соответствие не должно содержать пар
с одинаковыми вторыми и различными
первыми координатами). Пар с одинаковыми
вторыми и различными первыми координатами
в данном соответствии не имеется,
следовательно, оно инъективно.
3.
Найдем образ
и прообраз
при соответствии
.
Так как
,
а элементы
и
образуют в исходном соответствии
подмножество
,то образ
.
Так как
,
а один элемент 4 образует в исходном
соответствии подмножество
,
топрообраз
.
4. Построим
соответствие между бесконечными
множествами, обладающее тем же набором
свойств, что и
.
Пусть
,
,
.
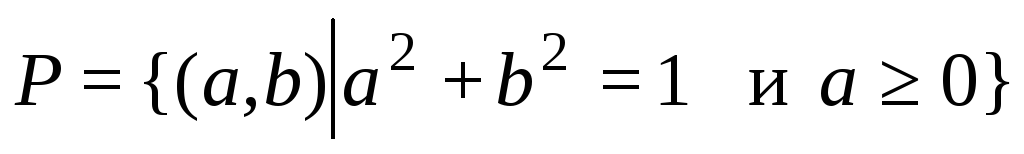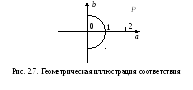
Графиком данного
соответствия будет полукруг (рис. 2.7),
из которого видно, что
,
,
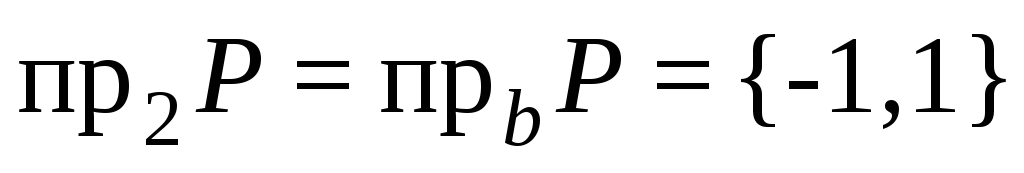а само соответствие в виде множества
.
а) Построенное
соответствие не
всюду определено,
так как
.
б)
Построенное
соответствие не
сюръективно,
так как
.
а) Построенное
соответствие не
всюду определено,
так как
.
б)
Построенное
соответствие не
сюръективно,
так как
.
в)
Построенное
соответствие не
функционально,
так как содержит пары с одинаковыми
первыми и различными вторыми координатами,
например,
и
.
г) Соответствие инъективно, так как не содержит пар с различными первыми и одинаковыми вторыми координатами.
5. Построим соответствие между конечными множествами, обладающее набором свойств, противоположным исходному, то есть такое, чтобы оно было всюду определено, сюръективно, функционально, не инъективно.
Пусть
,
,
.
Векторная диаграмма данного соответствия
представлена на рис. 2.8.
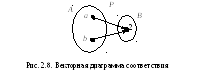
а)
Данное
соответствие всюду
определено,
так как
.
б)
Соответствие сюръективно,
так как
.
в) Соответствие функционально, так как оно не содержит пар с одинаковыми первыми и различными вторыми координатами.
г)
Соответствие не
инъективно,
так как содержит две пары
и
с одинаковыми вторыми и различными
первыми координатами.
Так как построенное
соответствие всюду определено, сюръективно
и функционально, то оно является
отображением
на
.
5.
Дано отношение
,
заданное на множестве
(табл. 2.2).
1. Выяснить, какими
из свойств: рефлексивность,
антирефлексивность, симметричность,
антисимметричность, транзитивность,
связность обладает отношение
,
заданное на множестве
.
2. Построить на конечном множестве отношение, обладающее таким же набором свойств, что и данное.
3. Построить на бесконечном множестве отношение, обладающее набором свойств, противоположным данному. В случае невозможности построения доказать противоречивость набора требований.
Пример решения задания 5
Вариант 9