2.1.2. Соответствие. Функция

Соответствие между множествами А и В – это множество, представляющее собой некоторое подмножество их декартова произведения

.

Полное соответствие между множествами А и В – это множество, равное их декартовому произведению

.

Если то говорят, что соответствуетв соответствии , (или они находятся в соответствии Р). Обозначается:или,,.

Соответствие предполагает, что некоторым элементам множества A (возможно, всем) поставлены в соответствие некоторые элементы множества B.

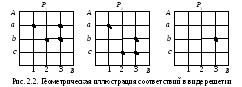
Соответствие, как и декартово произведение, можно изобразить графически в виде решетки или в виде векторной диаграммы. В узлах решетки оказываются соответствующие пары элементов декартова произведения.

Пусть имеются множества и. Декартово произведение будет представлять собой следующую последовательность

.

Из нее можно взять любые компоненты, которые и будут представлять собой соответствие из А в В, например

,,.

График соответствия для данных множеств представлен на рис. 2.2.

В виде векторной диаграммы соответствия представлены на рис. 2.3.

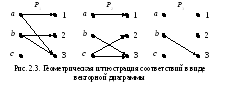
Образ элемента в множествепри соответствии– множество всех , соответствующих элементу.Обозначается .

Прообраз элемента в множествепри соответствии– множество всех , соответствующих элементу.Обозначается . Таким образом, если , то образ , а–прообраз .

Область определения соответствия Р (обозначается или) – множество таких ,для которых существует образ.

Область значений соответствия Р (обозначается или) – множество таких ,для которых существует прообраз.

Всюду определенное соответствие – соответствие, при котором выполняется равенство . В противном случае соответствие называется частичным.

Сюръективное соответствие (сюръекция) – соответствие, при котором выполняется равенство .

Инъективное соответствие (инъекция) – соответствие, при котором прообразом любого элемента из множества является единственный элемент из множества (соответствие не содержит пар с одинаковыми вторыми и различными первыми координатами).

Функциональное соответствие (функция) – соответствие , при котором образом любого элемента из множества является единственный элемент из множества (соответствие не содержит пар с одинаковыми первыми и различными вторыми координатами).

Взаимнооднозначное соответствие – соответствие, которое функционально и инъективно, то есть или .

Биекция (1-1 соответствие) – соответствие, которое всюду определено, сюръективно, функционально и инъективно.

Отображение в – соответствие, которое всюду определено и функционально.

Отображение на – соответствие, которое всюду определено, функционально и сюръективно.

Равномощные множества – множества, между которыми можно установить биекцию.

Счетное множество – множество, равномощное множеству натуральных чисел.

Континуальное множество – множество, равномощное множеству действительных чисел отрезка .

Пример 2.6.

Дано соответствие между (осью абсцисс) и (осью ординат) в виде круга радиуса1 с центром в точке (3, 2) (рис. 2.4), то есть в виде множества пар действительных чисел , удовлетворяющих соотношению.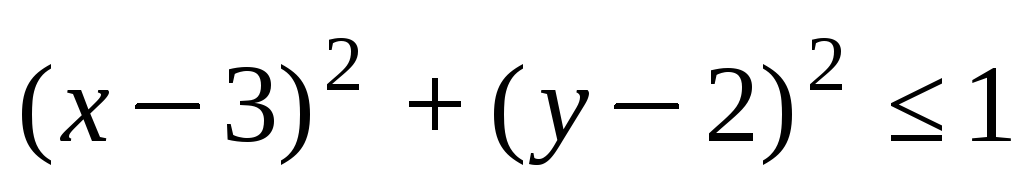

Образом в данном соответствии для числа 4 (ось абсцисс) является единственное число 2 (ось ординат), образом числа 3 является уже отрезок [1, 3] оси ординат.

Прообразом отрезка [1, 3] (ось ординат) является отрезок [2, 4] (ось абсцисс).

Данное соответствие не является функциональным, поскольку для такого соответствия необходимо, чтобы образом любого элемента из множества являлся единственный элемент из множества . Здесь множество это множество всех действительных чисел (ось абсцисс), каждому из которых может соответствовать не единственный образ из множества – множества всех действительных чисел (ось ординат).

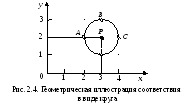
Примером функционального соответствия на том же рис. 2.4 могут служить дуги окружности, координаты которых каждой единственной точке на оси абсцисс ставят в соответствие единственную точку на оси ординат. В частности это могут быть дуги ,или.

Отметим, что в общем случае для задания соответствия необходимо указать не только множество , но и множества , то есть указать,подмножеством какого прямого произведения является . В данном примере тот же круг задает и другое соответствие:между отрезком [2, 4] и отрезком [1, 3]. При этом по некоторым свойствам соответствия и×отличаются: так второе соответствие в отличие от первого всюду определено и сюръективно, то есть и . Учитывая это, соответствие необходимо было бы определять как тройку множеств , и тогда не было бы необходимости оговариваться, что один круг может задавать два соответствия, поскольку это и так было бы ясно из-за различия троек и. Однако такие оговорки обычно делаются редко, так как либо множества ясны из контекста, либо различия в из выборе не влияют на исследуемые свойства соответствия. Поэтому определение соответствия через тройку множеств здесь использоваться не будет.

Пример 2.7.

Соответствие в виде словаря. Например, русско-английский словарь устанавливает соответствие между множеством русских и английских слов. Это соответствие не функционально, так как одному русскому слову обычно ставится в соответствие несколько английских слов. Кроме того, оно практически никогда не является полностью определенным, так как всегда можно найти русское слово, не содержащееся в данном словаре.

Пример 2.8.

Соответствие в виде шахматной позиции. Конкретная позиция на шахматной доске представляет собой взаимнооднозначное соответствие между множеством оставшихся на доске фигур и множеством занятых ими полей.

Пример 2.9.

Соответствие в виде кодирования. Кодирование букв азбукой Морзе, представление чисел в различных системах исчисления, секретные шифры, входящие и исходящие номера в деловой переписке, различные классификации и др. – являются соответствиями между кодируемыми объектами и присваиваемым им кодами.

Данные соответствия обычно обладают всеми свойствами взаимнооднозначного соответствия, кроме одного – сюръективности (), которое в некоторых случаях может не выполняться.

Так единственность образа и прообраза в кодировании гарантирует однозначность шифровки и дешифровки. Отсутствие сюръективности означает, что не всякий код имеет смысл, то есть соответствует какому-либо объекту. Так, кодирование городских телефонов номерами не сюръективно, так некоторые номера не соответствуют никаким телефонам.