3. Динамические свойства преобразователей

При выборе преобразователей для измерения переменных во времени величин (давления, ускорения и т. п.) нужно помнить о погрешностях, связанных с динамическим режимом работы пре- образователей и обусловленных их инерционными свойствами.

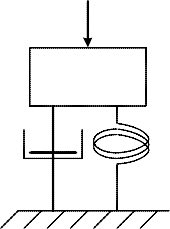
Общий вид модели измерительного преобразователя представлен на рис. 3.8.

F(t)

m

P W

A

Рис. 3.8. Физическая модель измерительного преобразователя:

F(t) – внешняя переменная сила; Р – демпфер (успокоитель); W – пружина

Внешняя переменная сила F(t) действует на массу m связан- ную с неподвижным телом А упругим элементом (например, пружиной W).

В преобразователях такого вида могут быть погрешности двух типов: амплитудная и фазовая.

Амплитудная погрешность. Если к массе m приложена пе- ременная сила F(t), то при ее действии амплитуда колебаний мас- сы m оказывается больше по сравнению с амплитудой перемеще- ния ее при единичном воздействии силы. Исследования уравне- ниядвиженияподвижнойчасти преобразователей в динамиче- ском режиме, при синусоидальном законе изменения силы F(t), дали кривые зависимости∆=f(λ)(рис. 3.9).

Амплитудная погрешность вынужденных колебаний – откло- нение наибольшей амплитуды колебаний в динамическом режи- ме (вынужденные колебания) к амплитуде перемещения подвиж- ной части при единичном воздействии силы:

^{X} max ä ^{/ X} max åä^.

Δ 5,5

5,0

4,5

4,0

3,5

3,0

2,5

2,0

1,5

1,0

0,5

β=1,0

β=0

β=0 β=0,2

β=0,4

β=0,6

β=0,7

β=0,8

0 0,5 1,0 1,5 2,0 λ

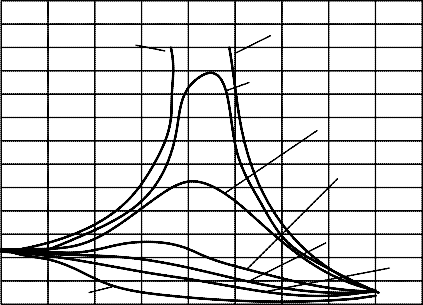
Рис. 3.9. Амплитудная погрешность преобразователей

При синусоидальном колебании подвижной части амплитуд- ная погрешность:

_2

 ,

² 1² 4² ²

где λ = ω/ω₀ (ω, ω₀ угловая частота вынужденных и собственных колебаний подвижной части соответственно); β – степень успоко- ения подвижной части.

Степень успокоения можно вычислить поформуле

P / P_êð ,

где Р_кр – коэффициент успокоения при критическом режиме дви- жения массы, т.е. при наименьшем времени успокоения.

По графикам на рис. 3.9 видно, что максимальная амплитуд- ная погрешность имеет место при λ = 1, т.е. при резонансе (ω = ω₀). Поэтому преобразователи перемещений и сил, работа- ющие в динамическом режиме, должны иметь λ = ω/ω₀ много меньше единицы, т.е. должны иметь собственную частоту ω₀ больше частоты измеряемого процесса ω.

Если собственная частота преобразователя ω₀ будет меньше частоты измеряемого процесса ω, то деталь (масса m) может вы- ходить из соприкосновения с силой F и измерения будут невер- ные. На рис. 3.9 видно, что амплитудная погрешность ∆ зависит также от степени успокоения подвижной части преобразователя и имеет наименьшее значение при β=0,6...0,7.

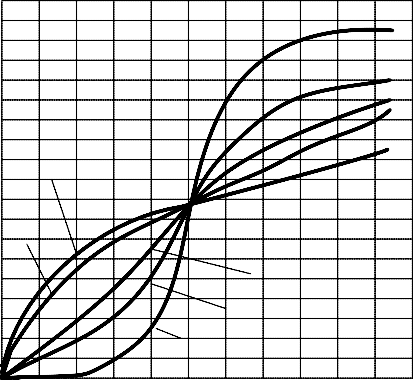
Фазовая погрешность. Фазоваяпогрешность выражается в запаздывании вынужденных колебаний подвижной части от ко- лебаний измеряемой величины (рис. 3.10).

ψ

150

120

90

60

30

β=2,0 β=1,0

β=0,7 β=0,5

β=0,1

0 0,2 0,6 1,0 1,4 1,8 λ

Рис. 3.10. Фазовая погрешность преобразователей

Очевидно, что при β =0,7 изменение фазовой погрешности име- ет почти линейную зависимость от λ, а также ψ меньше при малом λ. Фазовая погрешность может быть вычислена по формуле

arctg ^2.

² 1

Таким образом, при измерении переменных во времени ме- ханических величин во избежание больших амплитудных и фазовых погрешностей важно так подобрать параметры преоб-

разователя, чтобы обеспечить соответствующее соотношение частоты собственных колебаний преобразователя и частоты измеряемого процесса (вынужденных колебаний), а также сте- пень успокоения подвижной части преобразователя β = 0,6...0,7.

Погрешности системы преобразования. Основная погреш- ность прибора, состоящего из цепи измерительных преобразова- телей, складывается главным образом из двух составляющих:

• инструментальной погрешности, обусловленной погрешно- стями элементов, входящих в каждое звено (например, погреш- ность подгонки сопротивлений, трение в подвижных частях ме- ханизма, недостаточная тщательность исполнения деталей звена);

• погрешности из-за недостаточной чувствительности усили- теля и индикаторов.

Каждое из звеньев вносит свою долю в результирующую ос- новную погрешность прибора, причем при прямом преобразова- нии всезвенья равноправны в отношении степени влияния на общую погрешность. Поэтому всегда стремятся к уменьшению числа звеньев цепи преобразования.

Точность измерения неэлектрической величины зависит также и от ряда дополнительных факторов, которые необходимо учи- тывать. К ним относятся изменения величины напряжения, ча- стоты и формы кривой напряжения питания, изменение окружа- ющей температуры, влажности и вибрации.

Влияние дополнительных погрешностей можно оценить чув- ствительностью каждого звена к тому или иному влияющему фактору, т.е. отношением изменения выходной величины преоб- разователя данного звена к изменению дополнительного фактора (относительно его значения при градуировке).

Дополнительные факторы вызывают дополнительную состав- ляющую погрешности нуля и чувствительности прибора. Дей-

ствительно, изменение питающего напряжения вызывает появле- ние погрешности чувствительности во всех мостовых цепях (кроме равновесных мостов). В усилителях изменение питающего напряжения также вызывает некоторое изменение чувствитель- ности.

При изменении температуры изменяются жесткость упругих элементов, индукция постоянных магнитов, магнитные свойства ферромагнитныхматериалов. Кроме того, погрешность нуля и чувствительности прибора может быть вызвана изменением во времени параметров отдельных элементов схемы, шумами в эле- ментах схемы, наводкамипромышленной частоты и т.д.

Для уменьшения дополнительных погрешностей прибегают к стабилизации напряжения и частоты источников питания, к раз- ным приемам коррекции этих погрешностей и особенно заботят- ся о стабильности во времени физических свойств и параметров элементов прибора.

Кроме того, при анализе погрешностей сложных измеритель- ных устройств, состоящих из целого ряда самостоятельных зве- ньев, не всегда можно строго разграничить погрешности на си- стематические и случайные. Например, погрешность измерения от колебаний напряжения питающей сети с первого взгляда пред- ставляется систематической, так как на каждые ±10 % питающего напряжения прибор может иметь ±1 % изменения чувствительно- сти. Однако мгновенные изменения питающего напряжения сети происходят хаотически, и погрешность измерения, возникающая из-за этого, хотя и является однозначной функцией этого напря- жения, но будучи функцией случайной величины, представляет собой также случайную величину.

Это сильно затрудняет суммирование погрешностей измери- тельных устройств. Поэтому при анализе и выборе метода и сум- мирования погрешностей сложных измерительных устройств

следует подразделять погрешности не на систематические и слу- чайные, а по признаку их сильной или слабой взаимной корреля- ционной связи. Если ряд погрешностей одного или нескольких преобразователей вызывается одной общей причиной, в резуль- тате чего они оказываются сильно связаны между собой, то эти погрешности будут распределены по одному и тому же закону, а форма результирующего закона распределения будет также соот- ветствовать этому закону. Поэтому внутри каждой из этих групп погрешности должны складываться алгебраически с учетом их знака.

Результирующие погрешности, полученные после суммирова- ния в каждой из групп, уже не имеют между собой сильных кор- реляционных связей и должны рассматриваться как независимые и, следовательно, должны складываться геометрически.