plan_exp

В этом плане предмет заменен фактором. Нетрудно заметить, что план Хаутелинга обладает свойством симметричности.

Такие планы применяются лишь для отсеивающего эксперимента, так как они не дают возможности оценить линейные взаимодействия между факторами.

3. ПЛАНЫ ВТОРОГО ПОРЯДКА

Если математическая модель, полученная с помощью плана первого порядка неадекватна, то необходимо переходить к планам более высокого, например второго порядка. К таким планам относятся ортогональные [27], (в том числе Хартли [37]) и ротатабельные планы [19].

Наиболее простыми являются ортогональные планы они применяются тогда, когда достаточно точно известна область оптимума. Наиболее универсальны ротатабельные планы. Их применение с наибольшей вероятностью обеспечивает получение адекватных моделей, хотя формулы для определения коэффициентов при использовании этих планов более сложны. Планы Хартли, представляющие собой разновидность ортогональных планов, хотя и с меньшей вероятностью обеспечивают получение

адекватных моделей, используются в тех случаях, когда стремятся получить модель процесса при наименьших затратах времени и средств на проведение эксперимента.

Особенность практически всех планов второго порядка состоит в ,томчто в них полный или дробный факторный эксперимент является ядром планирования, к которому добавляют несколько точек, которые могут находиться как в центре, так и на периферии.

3.1. Ортогональные планы

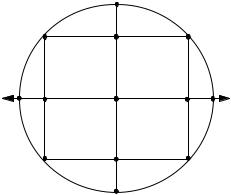
Начнем с двухфакторного эксперимента, ядром которого является план ПФЭ типа 22. Точки такого плана были показаны на рис.2. Дополним этот план точкой в центре эксперимента и четырьмя точками, расположенными на координатных осях на расстоянииa от начала координат (точки 6, 7, 8, 9), как это показано на рис. 4. Координаты точек плана представлены в таблице 10.

Таблица 10.

8

-a

Рис. 4

Левая часть плана, ограниченная жирной линией, представляет собой симметричный план. Если такой план дополнить столбцамиХ12 и Х 22 , то он теряет свойство симметричности, т.к. в нем будут

присутствовать только положительные величины. Поэтому симметричность плана создадим искусст-

Если план обладает свойством ортогональности, то сумма произведений величин в двух столбцах тоже, равна нулю. Составим столбец из произведений ( Х12 - X$ )( Х22 - X$ ). Тогда

Решая совместно (35) и (36), получим значения X$ и a, при которых план является и ортогональным, и симметричным.

Для определения коэффициентов регрессии можно воспользоваться следующими формулами

N

å yn

Выражения (35a) и (36a) позволяют определить X$ и a для любого числа факторов. Эти значения приведем в таблице 11.

Табл. 11.

Значения параметров ортогональных планов в зависимости от числа факторов.

Помимо a и X$ , в таблице приведены значения суммы в знаменателе выражений для определения квадратичных коэффициентов регрессии по формуле

N

å( Xin2 - X$ ) 2

n=1

атакже общее число опытов, составляющих план для различного числа факторов:

Формулы для определения линейных коэффициентов регрессии и коэффициентов при взаимодействиях для К факторов имеют вид:

Отсюда следует, что постоянный коэффициент модели для двух факторов:

В общем случае для любого числа факторов К:

i=1

3.2. Планы Хартли

Планы Хартли являются разновидностью ортогональных планов. Однако, в отличие от планов, рассмотренных в предыдущем параграфе, ядром плана здесь служит не полный, а дробный факторный эксперимент, в котором некоторые линейные эффекты коррелируют с линейными взаимодействиями.

Кроме того, в дополнительных точках опыты ставятся вm повторностях, каждая из которых имеет права опыта. В таблице 12 приведен план для трех факторов, составленный на базе ДФЭ типа23-1, в

котором используется генерирующее соотношение Х=Х Х . Опыты в точках с 5-ой по 11-ую прово-

3 1 2

дятся в m повторностях. Поэтому

Если m=3, то общее число опытов (строчек плана) N = 23-1 + 3(2× 3 + 1) = 25

Таблица 12

План Хартли для трех факторов