
- •Вариант 1.
- •Вариант 2.
- •1. Значение определителя равно:
- •7. Кривая второго порядка имеет центр симметрии в точке:
- •1. Значение определителя равно:
- •3. Решением системы уравнений является:
- •1. Значение определителя равно:
- •3. Решением системы уравнений является:
- •1. Значение определителя равно:
- •3. Решением системы уравнений является:
- •1. Значение определителя равно:
- •3. Решением системы уравнений является:
- •1. Значение определителя равно:
- •3. Решением системы уравнений является:
- •1. Значение определителя равно:
- •3. Решением системы уравнений является:
- •1. Значение определителя равно:
- •3. Решением системы уравнений является:
- •1. Значение определителя равно:
- •3. Решением системы уравнений является:
1. Значение определителя равно:
а) -22; б) 15; в) 16; г) 9.
2. Является ли матрица A
невырожденной
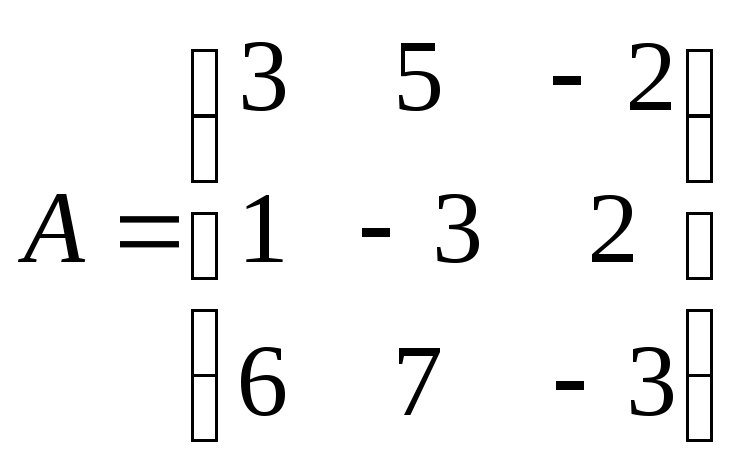 :
:
а)да; б) нет.
3. Решением системы уравнений является:
а) (1,2,3); б) (2,3,1); в) (2,1,-1); г) (2,2,3).
4. Сила F=(4,11,-6), приложенная к точке A(3,5,1), переместила ее в точку B(4,-2,-3), двигаясь прямолинейно. Найти работу.
а) 50; б) 49; в) 45; г) 40.
5. Векторное произведение векторов
![]() и
и
![]() равно:
равно:
а) 7; б) 17; в) (7,-7,7); г) (-7,7,7).
6. Уравнение медианы AD
![]() A(2,5), B(3,3),
C(-1,4), имеет вид:
A(2,5), B(3,3),
C(-1,4), имеет вид:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
7. Центр симметрии кривой второго порядка
![]() находится в точке:
находится в точке:
а) (3,1); б) (4,1); в) (1,2); г) (3,2).
8. При каком значении p
прямые
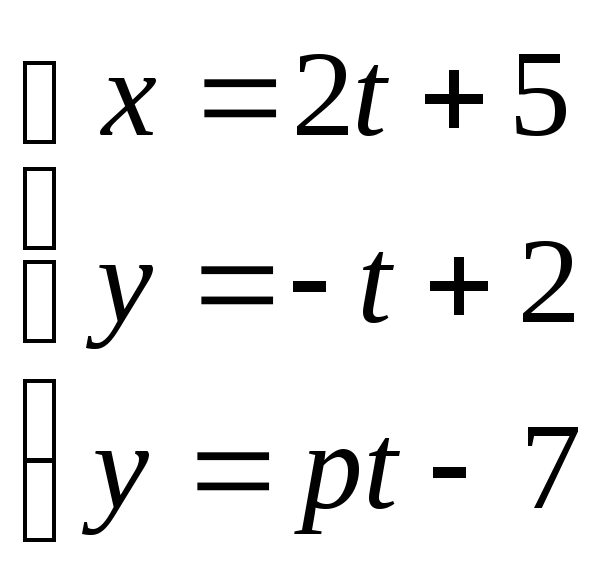 и плоскость
и плоскость
![]() параллельны:
параллельны:
а) -2; б) 3; в) -5; г) 5.
9. Прямая
![]() проходит через точку:
проходит через точку:
а) (4,-1,2); б) (-4,1,-2); в) (5,-1,-3); г) (-5,1,3).
10. Точки K и L
служат серединами сторон BC
и CD параллелограмма ABCD.
Положим
![]() ,
,
![]() то вектор
то вектор
![]() равен:
равен:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
ТЕСТ 1. Линейная алгебра и аналитическая геометрия.
ВАРИАНТ 8.
1. Значение определителя равно:
а) 15; б) 17; в) 0; г) 16.
2. Является ли матрица A
обратимой
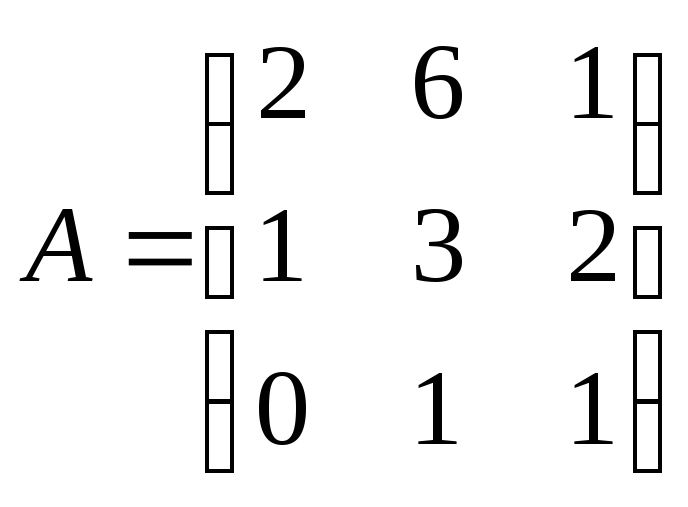 :
:
а) да: б) нет.
3. Решением системы уравнений является:
а) (1,2,2); б) (3,1,-1); в) (2,1,-1); г) (2,3,1).
4. Работа силы F=(-4,5,-7), приложенная к точке A(4,-2,3), переместила её в точку B(7,0,-3), двигаясь прямолинейно. Найти работу.
а) 40; б) 50; в) 75; г) 45.
5. Являются ли компланарными векторы
![]()
![]()
![]() :
:
а) да; б) нет.
6. Уравнение высоты AD ∆ABC, A(2,5), B(3,3), C(-1,4) имеет вид:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
7. Центр симметрии кривой второго порядка
![]() находится в точке:
находится в точке:
а) (1,1); б) (2,-1); в) (2,2); г) (1,0).
8. Прямая
![]() пересекает плоскость
пересекает плоскость
![]() в точке:
в точке:
а) (2,0,1); б) (2,3,4); в) (2.1,1); г) (3,1,2).
9. Направляющий ектор прямой
![]() имеет координаты:
имеет координаты:
а) (4,3,-1); б) (2,-1,0); в) (-4,-3,1); г) (-2,1,0).
10. Точки K и L
служат серединами сторон BC
и CD параллелограмма. Если
![]() ,
,
![]() ,
то вектор
,
то вектор
![]() равен:
равен:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
ТЕСТ 1. Линейная алгебра и аналитическая геометрия.
ВАРИАНТ 9.
1. Значение определителя равно:
а) 13; б) 24; в) –48; г) 48.
2. Какая из матриц является обратной
данной
![]() :
:
а)
![]()
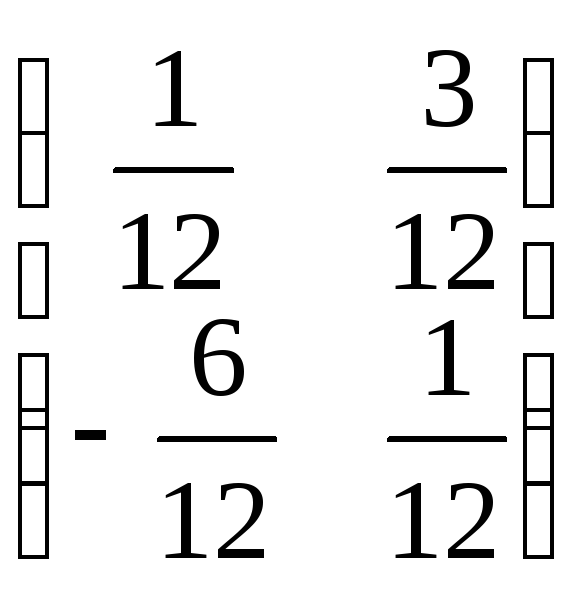 ;
б)
;
б)
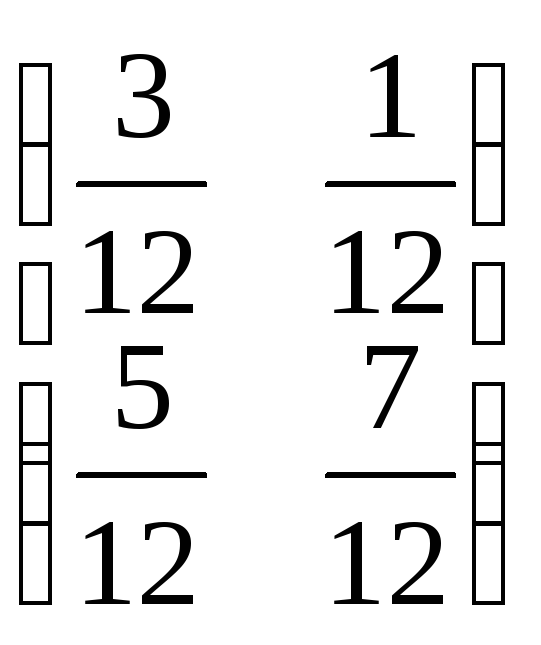 ;
в)
;
в)
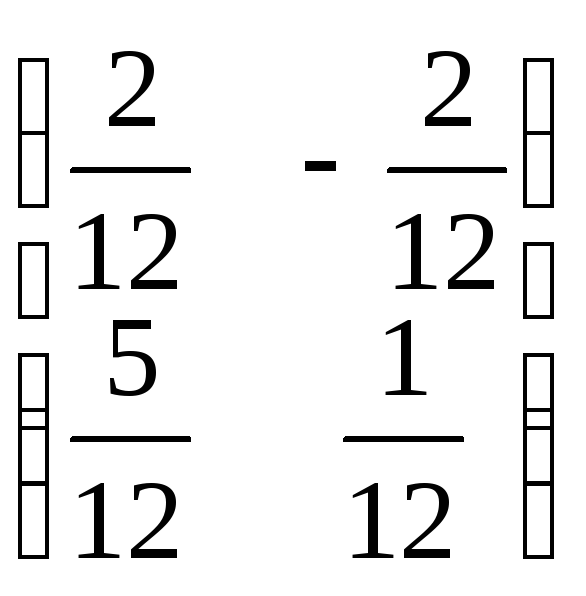 ;
г)
;
г)
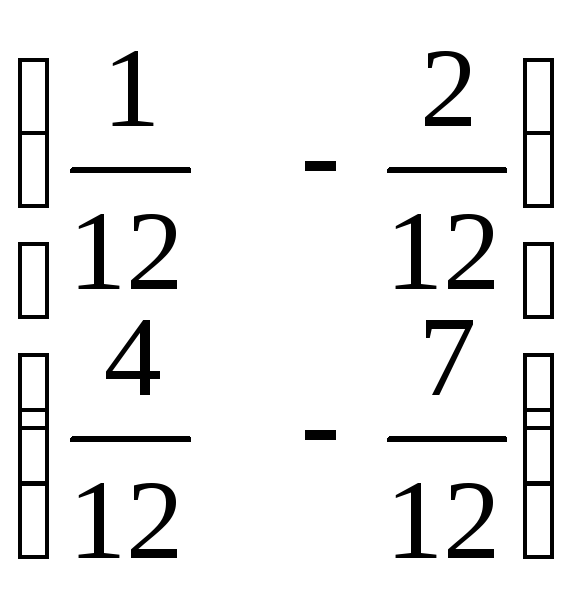 .
.
3. Решением системы уравнений является:
а) (1.2.3); б) (4,-3,1); в) (2,1,1); г) (1,-2,-3).
4. Работа силы F=(2,19,-4), приложенная к точке A(5,3,4), переместила её в точку B(6,-4,-1), двигаясь прямолинейно. Найти работу.
а) 102; б) 108; в) 111; г) 104.
5. Объём параллелепипеда, построенного
на векторах
![]()
![]()
![]() равен:
равен:
а) 18; б) 48; в) 6; г) 8.
6. Уравнение медианы AD ∆ABC, A(2,-3), B(1,0), C(-2,-4) имеет вид:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
7. Центр симметрии кривой второго порядка
![]() находится в точке:
находится в точке:
а) (0,2); б) (2,2); в) (1,1); г) (0,2).
8. При каких значениях n
и A прямая
![]() перпендикулярна плоскости:
перпендикулярна плоскости:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
9. Нормальный вектор плоскости
![]() имеет координаты:
имеет координаты:
а) (3,2,-1); б) (-2,-3,1); в) (2,3,-1); г) (2,1,5).
10. Точки K и L
служат серединами сторон BC
и CD параллелограмма ABCD.
Если
![]() ,
,
![]() ,
то вектор
,
то вектор
![]() равен:
равен:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
ТЕСТ 1. Линейная алгебра и аналитическая геометрия.
ВАРИАНТ 10.
