Умножение3

21

перемножить в любом порядке.

Методически данное правило имеет целью подготовить ребенка к знакомству со способами умножения в столбик чисел, оканчиваю­щихся нулями, поэтому с ним знакомятся только в четвертом клас­се. Реально данное свойство умножения позволяет рационализи­ровать устные вычисления как во 2, так и в 3 классе.

Например:

Вычисли: (7 • 2) • 5 = ...

В данном случае намного легче вычислить вариант

7 • (2 • 5) = 7 • 10 - 70.

Вычисли: 12 • (5 • 7) = ...

8 данном случае намного легче вычислить вариант (12-5)-7 = 60-7 = 420.

Приемы вычислений

1. Умножение и деление чисел, оканчивающихся нулем: 20 • 3; 3 • 20; 60 : 3; 80 : 20

Вычислительный прием в данном случае сводится к умноже­нию и делению однозначных чисел, выражающих число десятков в заданных числах. Например:

20 • 3 =... 3 • 20 =... 60:3 = ...

2 дес. • 3 = 20 • 3 = 60 б дес.: 3 = 2 дес.

20 - 3 = 60 3 • 20 = 60 60: 3 = 20

Для случая 80:20 может быть использовано два способа вычис­лений: тот, что использовался в предыдущих случаях, и способ под­бора частного.

Например: 80: 20 =... 80 : 20 =...

8 дес.: 2 дес. = 4 или 20 • 4 = 80

80: 20 = 4 80: 20 = 4

В первом случае использовался прием представления двузнач­ных десятков в виде разрядных единиц, что сводит рассматривае­мый случай к табличному (8:2). Во втором случае цифра частного находится подбором и проверяется умножением. Во втором случае ребенок возможно не сразу подберет верную цифру частного, это означает, что проверка будет выполнена не один раз.

2. Прием умножения двузначного числа на однозначное: 23 • 4; 4-23

При умножении двузначного числа на однозначное актуализи­руются следующие знания и умения:

В случае умножения вида 4 • 23 сначала применяется переста­новка множителей, а затем та же схема умножения, что и выше.

3. Прием деления двузначного числа на однозначное: 48:3; 48:2

При делении двузначного числа на однозначное актуализиру­ются следующие знания и умения:

В случае 48:2 = (40 + 8) : 2, а дальше аналогично предыдущему случаю. разрядные слагаемые

4. Прием деления двузначного числа на двузначное: 68 : 17

При делении двузначного числа на двузначное необходимы сле­дующие знания и умения:

68: 17 =

Сложность последнего приема состоит в том, что ребенок не может сразу подобрать нужную цифру частного и выполняет несколько прове­рок подобранных цифр, что требует достаточно сложных вычислений. Многие дети тратят много времени на выполнение вычислений этого вида, поскольку начинают не столько подбирать подходящую цифру частного, сколько перебирают все множители подряд, начиная с двух.

С целью облегчения вычислений могут быть использованы два приема:

1) ориентировка на последнюю цифру делимого;

2) прием округления.

Первый прием предполагает, что при подборе возможной циф­ры частного ребенок ориентируется на знание таблицы умноже­ния, сразу перемножая подобранную цифру (число) и последнюю цифру делителя.

Например, 3-7 = 21. Последняя цифра числа 68 — это 8, значит нет смысла умножать 17 на 3, последняя цифра делителя все равно не сов­падает. Пробуем в частном число 4 — умножаем 7 • 4 = 28. Последняя цифра совпадает, значит имеет смысл найти произведение 17 • 4.

Второй прием предполагает округление делителя и подбор циф­ры частного с ориентиром на округленный делитель.

Например, 68:17 делитель 17 округляется до 20. Примерная циф­ра частного 3 дает при проверке 20 • 3 = 60 < 68, значит имеет смысл сразу проверять в качестве цифры частного 4:17 • 4 = 68.

Эти приемы позволяют сократить затраты сил и времени при выполнении вычислений данного вида, но требуют хорошего зна­ния таблицы умножения и умения округлять числа.

Целые числа, оканчивающиеся цифрами 0,1,2,3,4, округляют до ближайшего целого десятка, отбрасы­вая эти цифры.

Например, числа 12, 13, 14 следует округлять до 10. Числа 62, 63, 64 округляют до 60.

Целые числа, оканчивающиеся цифрами 5, 6, 7,8,9, округляют до ближайшего целого десятка в большую сторону.

Например, числа 15,16,17,18,19 округляют до 20. Числа 45,47, 49 округляют до 50.

Порядок действий в выражениях, содержащих умножение и деление

Правила порядка выполнения действий задают основные при­знаки выражений, на которые следует ориентироваться при вычис­лении их значений.

Первые правила, определяющие порядок действий в арифме­тических выражениях, задавали порядок действий в выражениях, содержащих действия сложения и вычитания:

1. В выражениях без скобок, содержащих только действия сложения и вычитания, действия выполня­ются в том порядке, как они записаны: слева направо.

2. Действия в скобках выполняют первыми.

3. Если выражение содержит только действия сло­жения, то два соседних слагаемых всегда можно заме­нить их суммой (сочетательное свойство сложения).

В 3 классе изучаются новые правила порядка выполнения дей­ствий в выражениях, содержащих умножение и деление:

4. В выражениях без скобок, содержащих только умножение и деление, действия выполняются в том порядке, как они записаны: слева направо.

5. В выражениях без скобок умножение и деление выполняются раньше, чем сложение и вычитание.

При этом установка на выполнение действия в скобках первым сохраняется. Возможные случаи нарушения этой установки были оговорены ранее.

Правила порядка выполнения действий являются общими пра­вилами вычислений значений математических выражений (при­меров), которые сохраняются на протяжении всего периода изучения математики в школе. В связи с этим формирование у ре­бенка четкого понимания алгоритма порядка выполнения дейст­вий является важной преемственной задачей обучения математике в начальной школе. Проблема заключается в том, что правила по­рядка выполнения действий являются достаточно вариативными и не всегда однозначно заданными.

Например, в выражении 48-3 + 7 + 8 следует по общей уста­новке применять правило 1 для выражения без скобок, содержа­щего действия сложения и вычитания. В то же время, как вариант рациональных вычислений, можно использовать прием замены суммой части 7 + 8, поскольку после вычитания числа 3 из 48 по­лучится 45, к чему удобно прибавить 15.

Однако подобный разбор такого выражения в начальных клас­сах не предусмотрен, поскольку есть опасения, что при неадекват­ном понимании такого подхода ребенок будет применять его в случаях вида 72 - 9 - 3 + 6. В данном случае замена выражения 3 + 6 суммой невозможна, она приведет к неверному ответу.

Большая вариативность в применении всей группы правил и вариантов правил при определении порядка действий требует значительной гибкости мышления, хорошего понимания смысла математических действий, последовательности мыслительных дей­ствий, математического «чутья» и интуиции (математики называ­ют это «чувство числа»). Реально намного проще приучить ребенка жестко соблюдать четко установленный порядок анализа число­вого выражения с точки зрения тех признаков, на которые ориен­тировано каждое правило.

Определяя порядок действий, рассуждай так:

1) Если есть скобки, выполняю первым действие, за­писанное в скобках.

2) Выполняю по порядку умножение и деление.

3) Выполняю по порядку сложение и вычитание.

Данный алгоритм задает порядок действий достаточно одно­значно, хотя и с небольшими вариациями.

В этих выражениях порядок действии определен алгоритмом однозначно и является единственно возможным. Приведем другие примеры

После выполнения умножения и деления в данном примере можно было сразу к 54 прибавить 6, а из 18 вычесть 9, пбсле чего результаты сложить. Технически было бы значительно легче, чем путь, обусловленный алгоритмом, возможен изначально другой по­рядок действий в примере:

Таким образом, вопрос о формировании умения определять по­рядок действий в выражениях в начальной школе определенным образом противоречит необходимости обучать ребенка способам рациональных вычислений.

Например, в случае порядок действий определен алгоритмом абсолютно однозначно, при этом требует отребенка сложнейших вычислений в уме с переходами через разряд: 42 - 7 и 35 + 8.

2 1 3

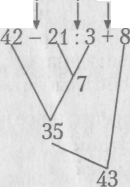
Если же после выполнения деления 21:3, выполнить сложение 42 + 8 = 50, а затем вычитание 50 - 7 = 43, что намного легче тех­нически, ответ будет тот же. Этот путь вычислений противоречит установке данного в учебнике