Физика. Задачи ВФ 1-2

1.3. Контрольная работа № 1.

Номер варианта соответствует номеру фамилии студента в журнале группы. Сроки сдачи работ указываются лектором. Решение задачи должно включать её условие, последовательное изложение процесса решения с комментариями, ответ в общем виде и численные расчёты в единицах СИ.

№ в журнале группы	Номера задач
1	101	111	121	131	141	151
2	102	112	122	132	142	152
3	103	113	123	133	143	153
4	104	114	124	134	144	154
5	105	115	125	135	145	155
6	106	116	126	136	146	156
7	107	117	127	137	147	157
8	108	118	128	138	148	158
9	109	119	129	139	149	159
10	110	120	130	140	150	160
11	101	112	121	132	141	152
12	102	111	122	131	142	151
13	103	114	123	134	143	154
14	104	113	124	133	144	153
15	105	116	125	136	145	156
16	106	115	126	135	146	155
17	107	118	127	138	147	158
18	108	117	128	137	148	157
19	109	120	129	140	149	160
20	110	119	130	139	150	159
21	110	111	130	131	150	151
22	101	120	121	140	141	160
23	109	112	129	132	149	152
24	102	119	122	139	142	159
25	108	113	128	133	148	153
26	103	118	123	138	143	158
27	107	114	127	134	147	154
28	104	117	124	137	144	157
29	105	116	125	136	145	156
30	106	115	126	135	146	155

101. Точка обращается по окружности радиусом R = 1,2 м. Уравнение движения точки  = At + Bt³, где A = 0,5 рад/c, В = 0,2 рад/с³. Определить тангенциальное a_ , нормальное a_n и полное a ускорения точки в момент времени t = 4 с.

102. Определить скорость  и полное ускорение a точки в момент времени t = 2 с, если она движется по ок­ружности радиусом R = 1 м согласно уравнению  = At + Bt³, где A = 8 м/с, B = 1 м/с³;  – координата, отсчитанная от некоторой точки, принятой за начальную, вдоль ок­ружности.

103. По прямой линии движутся две материальные точки согласно уравнениям x₁ = A₁ + B₁ t + C₁ t² и x₂ = A₂ + B₂ t + C₂ t² , где A₁ = 10 м, B₁ = 1 м/с, C₁ = 2 м/с², A₂ = 3 м, B₂ = 2 м/с, C₂ = 0,2 м/с². В какой момент времени t скорости этих точек будут одинаковы? Найти ускорения a₁ и a₂ этих точек.

104. Определить полное ускорение a в момент t = 3 с точки, находящейся на ободе колеса радиусом R = 0,5 м, вра­щающегося согласно уравнению  = At + Bt³, где A = 2 рад/c, В = 0,2 рад/с³ .

105. Точка обращается по окружности радиусом R = 8 м. В некоторый момент времени нормальное ускорение точки a_n = 4 м/с², вектор полного ускорения образует в этот момент с вектором нормального ускорения угол  = 60° . Найти скорость  и тангенциальное ускорение a_ точки.

106. Точка движется по прямой согласно уравнению x = At + Bt³, где A = 6 м/c, В =  0,125 м/с³. Определить среднюю путевую скорость < > точки в интервале времени от t₁ = 2 с до t₂ = 6 с.

107. Материальная точка движется прямолинейно. Уравнение движения имеет вид x = At + Bt³, где A = 6 м/c, В =  0,125 м/с³. Найти скорость  и ускорение a точки в моменты времени t₁ = 0 и t₂ = 3 с. Каковы средние значения скорости < _x > и ускорения < a_x > за первые 3 с движения?

108. Диск радиусом R = 0,2 м вращается согласно уравне­нию  = A + Bt + Ct³, где A = 3 рад, B = 1 рад/c, C = 0,1 рад/с³. Определить тангенциальное a_ , нормальное a_n и полное a ускорения точек на окружности диска для момента времени t = 10 c.

109. Точка движется по окружности радиусом R = 4 м. Закон её движения выражается уравнением s = A + B t² , где A = 8 м, B = 2 м/с² . Найти момент времени t, когда нормальное ускорение точки a_n = 9 м/с² ; скорость  , тангенциальное a_ и полное a ускорения точки в этот момент времени.

110. Колесо радиусом R = 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени задаётся уравнением  = A + Bt + Ct³, где B = 2 рад/c, C = 1 рад/с³. Для точек, лежащих на ободе колеса, найти через 2 с после начала движения следующие величины: 1) угловую скорость, 2) линейную скорость, 3) угловое ускорение, 4) тангенциальное ускорение, 5) нормальное ускорение.

111. Определить скорость поступательного движения сплош­ного цилиндра, окатившегося с наклонной плоскости высотой h = 20 см .

112. Тонкостенный цилиндр с диаметром основания D = 30 см и массой m = 12 кг вращается согласно уравнению  = A + Bt + Ct³, где A = 4 рад, B = 2 рад/c, C = 0,2 рад/с³. Определить действующий на цилиндр момент сил M в момент времени t = 3 с.

113. На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг. Опреде­лить момент инерции I маховика, если он, вращаясь равно­ускоренно под действием силы тяжести груза, за время t = 3 с приобрёл угловую скорость  = 9 рад/с .

114. Нить с привязанными к её концам грузами массой m₁ = 50 г и m₂ = 60 г перекинута через блок диамет­ром D = 4 см. Определить момент инерции блока, если под действием силы тяжести грузов он получил угловое ускорение  = 1,5 рад/с².

115. Тело вращается вокруг неподвижной оси согласно урав­нению  = At + Bt³, где A = 2 рад/c, B = 0,2 рад/с³. Определить вращающий момент M, действующий на тело в мо­мент времени t = 2 с, если его момент инерции I = 0,048 кгм² .

116. Определить момент силы M, который необходимо приложить к блоку, вращающемуся с частотой n = 12 с^1, чтобы он остановился в течение времени t = 8 с. Диаметр блока D = 30 см. Массу блока m = 6 кг считать равномерно распределённой по ободу.

117. Блок, имеющий форму диска массой m = 4 кг, враща­ется под действием силы натяжения нити, к концам которой подвешены грузы массой m₁ = 0,3 кг и m₂ = 0,7 кг. Определить силы F₁ и F₂ натяжения нити по обе стороны блока.

118. Сплошной цилиндр, расположенный горизонтально, может враща­ться около оси, совпадающей с осью цилиндра. Масса цилиндра m₁ = 12 кг. На цилиндр намотали шнур, к которому привязали гирю массой m₂ = 1 кг. С каким ускорением будет опус­каться гиря? Какова сила натяжения шнура во время движения гири?

119. По касательной к шкиву маховика в виде диска диа­метром D = 75 см и массой m = 40 кг приложена сила F = 1 кН. Определить угловое ускорение  и частому вращения n маховика через время t = 10 с после начала действия силы, если радиус r шкива равен 12 см. Силой трения пренебречь.

120. Двум одинаковым маховикам, находящимся в покое, сообщили одинаковую угловую скорость  = 63 рад/с и предос­тавили их самим себе. Под действием сил трения первый маховик оста­новился через одну минуту, а второй сделал до полной оста­новки N = 360 оборотов. У какого маховика тормозящий момент был больше и во сколько раз?

121. На краю платформы в виде диска диаметром D = 2 м, вращающейся по инерции вокруг вертикальной оси с частотой n₁ = 8 мин^1, стоит человек массой m₁ = 70 кг. Когда человек перешёл в центр платформы, она стала вращаться с час­тотой n₂ = 10 мин^1. Определить массу m₂ платформы. Мо­мент инерции человека рассчитывать, как для материальной точки.

122. Во сколько раз и почему увеличилась кинетическая энергия платформы с человеком в условиях предыдущей задачи?

123. На краю горизонтальной платформы в виде диска радиу­сом R = 1 м и массой m₁ = 10 кг стоит человек массой m₂ = 60 кг. С какой угловой скоростью  начнёт вращаться платформа, если человек поймает летящий на него мяч массой m = 0,5 кг? Траектория мяча горизонтальна, направлена по касательной к окружности диска. Скорость мяча  = 5 м/с.

124. Платформа в виде диска диаметром D = 3 м и мас­сой m₁ = 180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью ₁ будет вращаться эта плат­форма, если по её краю пойдёт человек массой m₂ = 70 кг со скоростью ₂ = 1,8 м/с относительно платформы?

125. На платформе стоит человек и держит в руках стер­жень вертикально по оси вращения платформы. Платформа с че­ловеком вращается с угловой скоростью ₁ = 4 рад/с. С какой угловой скоростью ₂ будет вращаться платформа с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и платформы I = 5 кгм². Длина стержня l = 1,8 м, его масса m = 6 кг. Считать, что центр тяжести стержня с человеком находится на оси платформы.

126. Человек стоит на платформе и держит в руках стержень вертикально вдоль оси вращения платформы. Стержень служит осью вращения колеса, расположенного на верхнем конце стерж­ня. Платформа неподвижна, колесо вращается с частотой n₁ = 15 с^1. С какой угловой скоростью ₂ будет враща­ться платформа, если человек повернёт стержень на угол  = 180° и колесо окажется на нижнем конце стержня? Суммарный момент инерции человека и платформы I = 8 кгм², радиус колеса R = 25 см. Массу колеса m = 2,5 кг можно считать равно­мерно распределённой по ободу. Считать, что центр тяжести че­ловека с колесом находится на оси платформы.

127. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол  повернётся платформа, если человек пойдёт вдоль края платформы и, обойдя её, вернётся в исходную (на платформе) точку? Масса платформы m₁ = 280 кг, масса человека m₂ = 80 кг. Момент инерции человека рассчитывать, как для материальной точки.

128. Шарик массой m = 60 г, привязанный к концу нити длиной l₁ = 1,2 м, вращается с частотой n₁ = 2 с^1, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик до расстояния l₂ = 0,6 м. С какой частотой n₂ будет при этом вращаться шарик? Какую работу A со­вершает внешняя сила, укорачивая нить? Трением шарика о плос­кость пренебречь.

129. Горизонтальная платформа массой 80 кг и радиусом 1 м вращается с угловой скоростью, соответствующей 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. Какое число оборотов в минуту будет делать платформа, если человек, опустив руки, уменьшит свой момент инерции от 2,94 кгм² до 0,98 кгм² ? Считать платформу круглым однородным диском.

130. Человек массой 60 кг находится на неподвиж­ной платформе массой 100 кг. Какое число оборотов в минуту будет делать платформа, если человек будет двигаться по окружности радиусом 5 м вокруг оси вращения? Скорость движения человека относительно платформы равна 4 км/ч. Радиус платформы 10 м. Считать платформу однородным диском, а человека – точечной массой.

131. Какая работа будет совершена силами тяготения при падении на поверхность Земли тела массой 2 кг: 1) с высоты h = 1000 км; 2) из бесконечности?

132. Из бесконечности на поверхность Земли падает метео­рит массой m = 30 кг. Какая работа при этом будет совершена силами тяготения Земли? Считать известными ускорение g свободного падения у поверхности Земли и её радиус R .

133. На какую высоту h над поверхностью Земли подни­мется ракета, пущенная вертикально вверх, если начальная скорость  ракеты будет равна первой космической скорости?

134. Во сколько раз кинетическая энергия искусственного спутника Земли, движущегося по круговой траектории, меньше его гравитационной потенциальной энергии?

135. Пружина жёсткостью k = 500 Н/м сжата силой F = 100 Н. Определить работу A внешней силы, дополнительно сжимаю­щей эту пружину ещё на l = 2 см.

136. Две пружины жёсткостью k₁ = 0,5 кН/м и k₂ = 1 кН/м скреплены последовательно. Определить потенциальную энергию  данной системы при абсолютной деформации l = 4 см.

137. Какую нужно совершить работу A, чтобы пружину жёсткостью k = 800 Н/м, сжатую на x = 6 см, дополнитель­но сжать на x = 8 см?

138. Если на верхний конец .вертикально расположенной спиральной пружины положить груз, то пружина сожмётся на l = 3 мм. На сколько сожмёт пружину тот же груз, упав­ший на конец пружины с высоты h = 8 см относительно её верхнего конца?

139. С поверхности Земли вертикально вверх пущена ракета со скоростью  = 5 км/с . На какую высоту она поднимается?

140. Налетев на пружинный буфер, вагон массой m = 16 т, двигавшийся со скоростью  = 0,6 м/с, остановился, сжав пружину на l = 8 см. Найти максимальную силу сжатия пру­жины.

141. Определить возвращающую силу F в момент вре­мени t = 0,2 с и полную энергию E точки массой m = 20 г, совершающей гармонические колебания согласно уравнению x = A sin  t , где A = 15 см,  = 4 с^1.

142. Определить максимальное ускорение a_max материа­льной точки, совершающей гармонические колебания с амплитудой A = 15 см, если наибольшая скорость точки _max = 30 см/с. Напи­сать также уравнение колебаний.

143. Найти максимальную кинетическую энергию E_Кmax материальной точки массой m = 2 г, совершающей гармоничес­кие колебания с амплитудой A = 4 см и частотой  = 5 Гц.

144. Материальная точка массой 10 г колеблется согласно уравнению 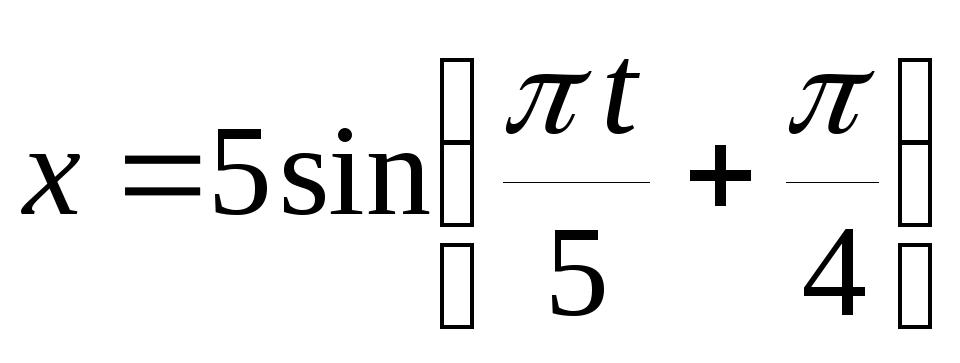см, t в с. Найти максимальную силу, действующую на точку, и полную энергию колеблющейся точки.

145. Точка совершает гармонические колебания. В некоторый момент времени смещение точки x = 5 см, её скорость  = 20 см/с и ускорение a = 80 см/с². Найти циклическую частоту и период колебаний; фазу колебаний в рассматривае­мый момент времени и амплитуду колебаний.

146. Точка совершает гармонические колебания, уравнение которых имеет вид x = A sin  t , где A = 5 см,  = 2 с^1. Найти момент времени (ближайший к началу отсчёта), в который потенциальная энергия точки E_П = 10^4 Дж, а возвращающая сила F = 510^3 Н. Определить также фазу колебаний в этот момент времени.

147. Поперечная волна распространяется вдоль упругого шнура со скоростью  = 15 м/с. Период колебаний точек шнура T = 1,2 с. Определить разность фаз  колебаний двух точек шнура, отстоящих от источника волн на расстояниях x₁ = 20 м и x₂ = 30 м.

148. Две точки находятся на прямой, вдоль которой расп­ространяется волна со скоростью  = 10 м/с. Период колебаний T = 0,2 с, расстояние между точками x = 1 м. Найти разность фаз  колебаний в этих точках.

149. Уравнение колебаний дано в виде y = sin 2,5 t см, t в с. Найти смещение от положения равновесия, скорость и ускорение точки, находящейся на расстоянии 20 м от источника колебаний, для момента t = 1 с после начала колебаний. Скорость распространения колебаний равна 100 м/с.

150. Уравнение колебаний дано в виде y = 10 sin 0,5 t см, t в с. 1) Найти уравнение волны, если скорость распространения коле­баний 300 м/с. 2) Какую разность фаз будут иметь колеба­ния двух точек, находящихся на расстоянии соответственно 10 м и 16 м от источника колебаний?

151. Определить частоту  гармонических колебаний диска радиусом R = 20 см около горизонтальной оси, проходя­щей через середину радиуса диска перпендикулярно его плос­кости.

152. Определить период T гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.

153. На стержне длиной l = 30 см укреплены два одинаковых грузика: один – в середине стержня, другой – на одном из его концов. Стержень с грузиками колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить период T гармонических колебаний. Массой стержня пренебречь.

154. Обруч диаметром 56,5 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти период этих колебаний.

155. Однородный стержень совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей через его верхний конец. Длина стержня l = 0,5 м. Найти период колебаний стержня.

156. Найти период колебаний стержня предыдущей задачи, если ось вращения проходит через точку, находящуюся на расстоянии 10 см от его верхнего конца.

157. На концах вертикального стержня укреплены два груза. Центр тяжести этих грузов находится ниже середины стержня на d = 5 см. Найти длину стержня, если известно, что период малых колебаний стержня с грузами вокруг горизонтальной оси, проходящей через его середину, T = 2 с. Массой стержня по сравнению с массой грузов пренебречь.

158. Определить период T колебаний стержня длиной l = 30 см около оси, перпендикулярной стержню и проходящей через его конец.

159. Однородный диск радиусом R = 30 см колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Определить период T ко­лебаний диска.

160. Диск радиусом R = 24 см колеблется около горизон­тальной оси, проходящей через середину одного из радиусов перпендикулярно к плоскости диска. Определить частоту  колебаний такого физического маятника.

2.3. Контрольная работа № 2.

№ в журнале группы	Номера задач
1	201	220	221	240	241	260
2	202	219	222	239	242	259
3	203	218	223	238	243	258
4	204	217	224	237	244	257
5	205	216	225	236	245	256
6	206	215	226	235	246	255
7	207	214	227	234	247	254
8	208	213	228	233	248	253
9	209	212	229	232	249	252
10	210	211	230	231	250	251
11	201	219	221	239	241	259
12	202	220	222	240	242	260
13	205	217	225	237	245	257
14	204	216	224	236	244	256
15	203	215	223	235	243	255
16	206	218	226	238	246	258
17	207	211	227	231	247	251
18	210	214	230	234	250	254
19	208	212	228	232	248	252
20	209	213	229	233	249	253
21	201	218	221	238	241	258
22	203	220	223	240	243	260
23	202	217	222	237	242	257
24	204	219	224	239	244	259
25	206	216	226	236	246	256
26	205	215	225	235	245	255
27	207	213	227	233	247	253
28	208	214	228	234	248	254
29	209	211	229	231	249	251
30	210	212	230	232	250	252