
- •Раздел 1. Матрицы и определители
- •Раздел 2. Системы линейных уравнений
- •Раздел 3. Векторы и линейные пространства. Линейные операторы.
- •Раздел 4. Координатный метод. Прямая и плоскость.
- •Раздел 5. Кривые второго порядка. Квадратичные формы.
- •Раздел 6. Алгебраические структуры
- •4.2. Комплекты дидактических материалов к проведению занятий Вычисление определителей. Решение систем линейных уравнений по формулам Крамера
- •Линейные операции над матрицами. Умножение матриц. Обратная матрица
- •Решение систем линейных уравнений матричным способом. Решение матричных уравнений
- •Ранг матрицы. Теорема Кронекера—Капелли .
- •Собственные векторы и собственные значения матрицы
- •Линейные операции над векторами. Линейная зависимость и независимость системы векторов. Базис
- •Скалярное произведение векторов, его вычисление, свойства и применения
- •Векторное и смешанное произведения векторов, их вычисление, свойства и применения
- •Векторное и смешанное произведения векторов, их вычисление, свойства и применения
- •Уравнения плоскости в. Взаимное расположение плоскостей
- •Уравнения прямой в. Взаимное положение прямых, прямой и плоскости
- •Решение задач, связанных с различными уравнениями прямой и взаимным расположением прямых на плоскости
- •Кривые второго порядка
- •4.4. 4.5.
Ранг матрицы. Теорема Кронекера—Капелли .
Решение систем линейных уравнений методом Гаусса.
1. Найти ранг матицы методом элементарных преобразований:
1.1.
 1.2.
1.2.

1.3.
 1.4.
1.4.

1.5.
 1.6.
1.6.

2. Найти ранг матрицы методом окаймляющих миноров и указать один из базисных миноров:
2.1.
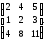 2.2.
2.2.
 2.3.
2.3.

3. Исследовать СЛУ и, если она совместна, найти решение методом
Гаусса:
3.1.
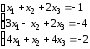 .3.2.
.3.2.
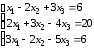 .
.
3.3.
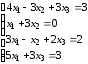 .3.4.
.3.4.
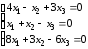 .
.
3.5.
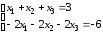 .3.6.
.3.6.
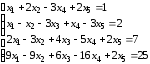 .
.
3.7.
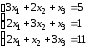 .
3.8.
.
3.8.
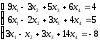

3.9.
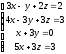 3.10.
3.10.
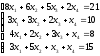
Дополнительные задания
Д-1. Найти ранг матрицы:
Д-1.1.
 Д-1.2.
Д-1.2.

Д-1.3.

Д-2. Найти ранг матрицы, содержащей параметр a:
Д-2.1.
 Д-2.2.
Д-2.2.
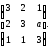 Д-2.3.
Д-2.3.
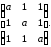
Д-3. Решить СЛУ методом Гаусса:
Д-3.1.
 .Д-3.2.
.Д-3.2.
 .
.
Д-3.3.
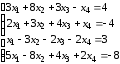 .Д-3.4.
.Д-3.4.
 .
.
Д-3.5.
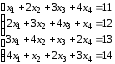 .Д-3.6.
.Д-3.6.
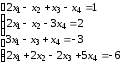 .
.
Д-3.7.
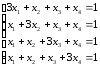 .Д-3.8.
.Д-3.8.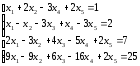 .
.
Д-4. Найти решение СЛУ, содержащей параметры:
Д-4.1.
 .Д-4.2.
.Д-4.2.
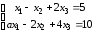 .
.
Д-4.3.
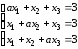 .Д-4.4.
.Д-4.4.
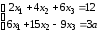 .
.
Д-5. Известно, что СЛУ совместна. Какому числу равен ранг расширенной системы?
Д-5.1.
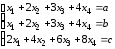 .Д-5.2.
.Д-5.2.
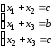 .
.
Д-5.3.
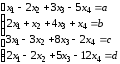 .Д-5.4.
.Д-5.4.
 .
.
Д-6. Решить СЛУ методом Гаусса:
Д-6.1.
 .Д-6.2.
.Д-6.2.
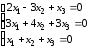 .
.
Д-6.3.
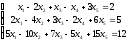 Д-6.4.
Д-6.4.
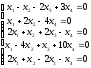
Итоговый самоконтроль
С-1. Изменится ли ранг матрицы при ее транспонировании?
С-2. Может ли ранг матрицы быть:
а) меньше нуля;
б) равным нулю;
в) равным 2,5;
г) больше числа строк матрицы;
д) меньше числа столбцов.
С-3. Изменится ли ранг матрицы при добавлении к ней строки, элементы которой пропорциональны элементам любой из имеющихся строк?
С-4.
Как отличаются ранги матриц
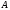 и
и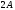 ?
?
С-5. Чему равен ранг матрицы, все строки которой пропорцио- нальны?
С-6. Может ли СЛУ иметь три решения? Одно решение?
С-7. Могут ли быть эквивалентными СЛУ, главные матрицы которых имеют равное число столбцов, но разное число строк?
С-8. Изменится ли решение системы, если к ней приписать уравнение?
С-9. Изменится ли решение несовместной системы, если к ней приписать уравнение?
С-10.
Если совокупность
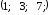 — решение однородной системы, можно ли
утверждать, что совокупность
— решение однородной системы, можно ли
утверждать, что совокупность![]() также является решением системы?
также является решением системы?
С-11.
Докажите, что если
![]() — ненулевое решение однородной системы
и
— ненулевое решение однородной системы
и![]() произвольное число, то и
произвольное число, то и![]() также является решением этой системы.
также является решением этой системы.
С-12. Что можно сказать о рангах матриц СЛУ, если они имеют одинаковое общее решение?
С-13.
Что можно сказать о СЛУ, если
![]() ,
,![]() ?
?
Собственные векторы и собственные значения матрицы
1. Найти собственные значения и собственные векторы матрицы:
1.1.
![]() .1.2.
.1.2.
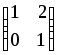 .
.
1.3.
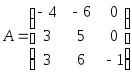 .1.4.
.1.4.
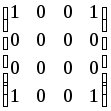 .
.
1.5.
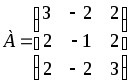 .1.6.
.1.6.
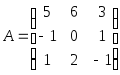 .
.
1.7.
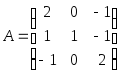 .1.8.
.1.8.
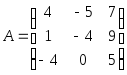 .
.
1.9.
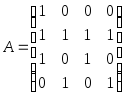 .1.10.
А
=
.1.10.
А
=
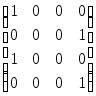
Дополнительные задания
Д-1. Определить собственные значения и собственные векторы матрицы:
Д-1.1.
 .Д-1.2.
.Д-1.2.
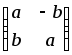 .
.
Д-2. Доказать, что собственные значения диагональной матрицы равны ее диагональным элементам.
Д-3.
Все собственные значения матрицы
![]() равны
равны![]() .
Найти все собственные значения матриц:
.
Найти все собственные значения матриц:
а)
![]() ;б)
;б)
![]() .
.
Д-4. Найти характеристические числа и собственные векторы матриц:
Д-4.1.
 .Д-4.2.
.Д-4.2.
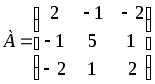 .
.
Д-4.3.
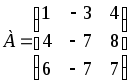 .Д-4.4.
.Д-4.4.
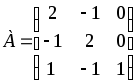 .
.
Д-4.5.
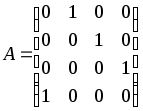 .Д-4.6.
.Д-4.6.
 .
.
Д-5.
Найти все векторы
![]() ,
удовлетворяющие уравнению
,
удовлетворяющие уравнению![]() ,
если матрица
,
если матрица![]() имеет вид:
имеет вид:
Д-5.1.
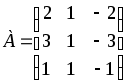 .Д-5.2.
.Д-5.2.
 .
.
Д-5.3.
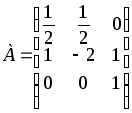 .
.
Д-6. Найти решения СЛУ при любых значениях параметра l:
Д-6.1.
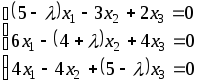 .Д-6.2.
.Д-6.2.
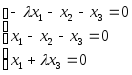 .
.
Итоговый самоконтроль
С-1. Чему равны собственные значения треугольной матрицы?
С-2. Имеет ли собственные значения вырожденная матрица?
С-3.
Что можно сказать о собственных значениях
матрицы
![]() ,
если известны собственные значения
матрицы
,
если известны собственные значения
матрицы![]() ?
?
С-4.
Верно ли утверждение о том, что все
n-мерные
векторы — являются собственными
векторами матрицы
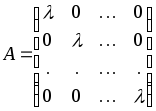 ?
?
С-5.
Что можно сказать о корнях характеристического
уравнения
![]() ,
если матрица
,
если матрица![]() симметрическая?
симметрическая?
С-6.
Если
![]() — собственные значения матрицы
— собственные значения матрицы![]() ,
то чему равны собственные значения
матриц
,
то чему равны собственные значения
матриц![]() ,
,![]() ?
?
