
- •Раздел 1. Матрицы и определители
- •Раздел 2. Системы линейных уравнений
- •Раздел 3. Векторы и линейные пространства. Линейные операторы.
- •Раздел 4. Координатный метод. Прямая и плоскость.
- •Раздел 5. Кривые второго порядка. Квадратичные формы.
- •Раздел 6. Алгебраические структуры
- •4.2. Комплекты дидактических материалов к проведению занятий Вычисление определителей. Решение систем линейных уравнений по формулам Крамера
- •Линейные операции над матрицами. Умножение матриц. Обратная матрица
- •Решение систем линейных уравнений матричным способом. Решение матричных уравнений
- •Ранг матрицы. Теорема Кронекера—Капелли .
- •Собственные векторы и собственные значения матрицы
- •Линейные операции над векторами. Линейная зависимость и независимость системы векторов. Базис
- •Скалярное произведение векторов, его вычисление, свойства и применения
- •Векторное и смешанное произведения векторов, их вычисление, свойства и применения
- •Векторное и смешанное произведения векторов, их вычисление, свойства и применения
- •Уравнения плоскости в. Взаимное расположение плоскостей
- •Уравнения прямой в. Взаимное положение прямых, прямой и плоскости
- •Решение задач, связанных с различными уравнениями прямой и взаимным расположением прямых на плоскости
- •Кривые второго порядка
- •4.4. 4.5.
Линейные операции над матрицами. Умножение матриц. Обратная матрица
1. Найти матрицу, заданную условием:
1.1.
 ,
если
,
если ,
,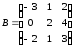 .
.
1.2.
 ,
если
,
если
 ,
, .
.
1.3.
 ,
если
,
если .
.
2.
Найти значение матричного многочлена
 ,
если:
,
если:
2.1.
 ,
,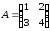 .
.
2.2.
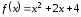 ,
, .
.
3. Проверить перестановочность матриц:
3.1.
 ,
, .
.
3.2.
 ,
, .
.
4.
Найти произведение
 и
и .
Существуют ли матрицы
.
Существуют ли матрицы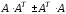 ?
?
4.1.
 .4.2.
.4.2.
 .4.3.
.4.3.
 .
.
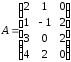
5. Привести матрицы к ступенчатому виду:
5.1.
 .5.2.
.5.2.
 .
.
5.3.
 .
.
6. Найти матрицу, обратную данной:
6.1.
 .6.2.
.6.2.
 .
6.3.
.
6.3.
 .
.
7. Найти обратную матрицу методом элементарных преобразований:
7.1.
 .7.2.
.7.2.
 7.3.
7.3.
 .
.
7.4.
 .7.5.
.7.5.
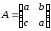 .
.
Дополнительные задания
Д-1.
Найти произведения
 и
и :
:
Д-1.1.
 ,
,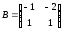 ,
, .
.
Д-1.2. ,
,  ,
, .
.
Д-2.
Найти матрицы
 и
и :
:
Д-2.1.
 .
. .
.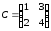 .
.
Д-2.2.
 .
. .
. .
.
Д-3.
Найти матрицу
 :
:
Д-3.1.
 .Д-3.2.
.Д-3.2.
 .Д-3.3.
.Д-3.3.
 .
.
Д-4.
Найти
 ,
если
,
если .
.
Д-5.
Найти матрицы, перестановочные с матрицей
 ,
если:
,
если:
Д-5.1.
 .Д-5.2.
.Д-5.2.
 .Д-5.3.
.Д-5.3.
 .
.
Д-6. Найти матрицу, обратную данной, с помощью присоединенной матрицы или методом элементарных преобразований:
Д-6.1.
 .Д-6.2.
.Д-6.2.
 .Д-6.3.
.Д-6.3.
 .
.
Д-6.4.
 .Д-6.5.
.Д-6.5.
 .Д-6.6
.Д-6.6 .
.
Д-7.
Вычислить матрицу
 ,
где
,
где ,
,
 ,
,
 .
.
Д-8.
Вычислить матрицу
 ,
где
,
где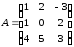 ,
, ,
, .
.
Д-9.
Вычислить
 ,
если
,
если .
.
Д-10.
Найти
 ,
если
,
если ,
, .
.
Д-11.
При каких значениях l
матрица
 не имеет обратной?
не имеет обратной?
Д-11.1. .
Д-11.2.
.
Д-11.2.
 .Д-11.3.
.Д-11.3. .
.
Итоговый самоконтроль
С-1. Следует ли из возможности сложения матриц возможность их перемножить и наоборот?
С-2. Можно ли умножить и в любом ли случае:
а)
матрицу-столбец на матрицу
 ;
;
б)
матрицу
 на матрицу-столбец;
на матрицу-столбец;
в)
матрицу-строку на матрицу
 ;
;
г)
матрицу
 на матрицу-строку;
на матрицу-строку;
д) матрицу-строку на матрицу-столбец;
е) матрицу-столбец на матрицу-строку.
С-3.
Можно ли найти квадрат матрицы, имеющей
размеры
 ?
?
С-4.
Каковы размеры матрицы
 ,
если известно, что
,
если известно, что ?
?
С-5.
Можно ли утверждать, что
 ?
?
С-6. Можно ли при умножении прямоугольных матриц получить квадратную матрицу?
С-7.
Можно ли утверждать, что
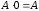 ?
?
С-8.
Верно ли утверждение
 ?
?
С-9. Верно ли утверждение: матрица, у которой пропорциональны соответственные элементы всех строк, эквивалентна нулевой?
С-10. Назовите наименьший размер матрицы.
С-11. Изменится ли произведение матриц при транспонировании одной из них?
С-12.
Верно ли утверждение, что
 ?
?
С-13.
Какие размеры имеет матрица, обратная
матрице размера
 ?
?
С-14.
Как изменится матрица
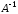 ,
если в матрице
,
если в матрице поменять местами две строки (столбца)?
поменять местами две строки (столбца)?
С-15.
Изменится ли матрица
 ,
если матрицу
,
если матрицу умножить на число
умножить на число ?
?
С-16.
Как изменится матрица
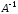 ,
если столбец или строку матрицы
,
если столбец или строку матрицы умножить на число
умножить на число ?
?
С-17. Является ли верным равенство:
а)
 ;б)
;б)
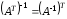 ;
;
в)
 ;г)
;г) .
.
С-18.
Каким общим свойством обладают матрицы
 и
и ?
?
Решение систем линейных уравнений матричным способом. Решение матричных уравнений
1. Решить матричным способом СЛУ:
1.1.
 .1.2.
.1.2.
 ;
;
1.3.
 .1.4.
.1.4.
 ;
;
1.5.
 .1.6.
.1.6.
 .
.
2. Решить матричное уравнение:
2.1.
 .2.2.
.2.2.
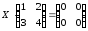 ;
;
2.3.
 .
2.4.
.
2.4.
 .
.
2.5.
 .
.
2.6.
 .
.
3. Найти все матрицы, удовлетворяющие уравнению:
3.1.
 .3.2.
.3.2.
 .
.
3.3.
 .3.4.
.3.4.
 .
.
3.5.
 .
.
Дополнительные задания
Д-1. Решить СЛУ матричным способом:
Д-1.1.
 .Д-1.2.
.Д-1.2.
 .
.
Д-1.3.
 .Д-1.4.
.Д-1.4.
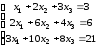 .
.
Д-1.5.
 .Д-1.6.
.Д-1.6. .
.
Д-2. Решить матричное уравнение:
Д-2.1.
 .
.
Д-2.2.
 .
.
Д-2.3.
 .
.
Д-2.4.
 .
.
Д-2.5.
 .
.
Д-3. Решить матричное уравнение:
 .
.
Д-4. Решить матричное уравнение:
Д-4.1.
 .Д-4.2.
.Д-4.2.
 .
.
Д-4.3.
 .
.
Итоговый самоконтроль
С-1. Может ли матричное уравнение иметь:
а) одно решение;
б) ни одного решения;
в) два решения.
Ответ поясните.
С-2.
Может ли уравнение
 иметь ненулевое решение?
иметь ненулевое решение?
С-3. Изменится ли решение СЛУ, если в основной матрице системы поменять местами две строки (два столбца)?
С-4. Верно ли, что:
а)
если
 ,
то
,
то ;
;
б)
если
 ,
то
,
то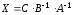 ;
;
в)
если
 ,
то
,
то .
.
С-5.
 матричная форма записи системы линейных
уравнений. Какое из выражений
матричная форма записи системы линейных
уравнений. Какое из выражений ,
, ,
, является решением системы?
является решением системы?
С-6. Решить матричные уравнения:
а)
 ;б)
;б)
 .
.
С-7. Можно ли говорить о сходстве решения СЛУ матричным способом и по формулам Крамера?
С-8. Решить матричное уравнение:
а)
 б)
б)
