Лекция 8. Индексы

Индексом называется относительная величина, которая характеризует изменение явления во времени или пространстве, а также степень выполнения плана.

Индексы получают в результате сравнения двух величин. При этом если сравнивается какая-то часть явления, то получаем индивидуальный индекс (i), если явление в целом, и при этом сопоставляются сложные показатели, то получаем общий (агрегатный) индекс (I):

; .

Агрегатные и средневзвешенные индексы

Для построения общих индексов несопоставимые показатели необходимо сделать сопоставимыми. Это достигается путём приведения к стоимости, затратам и некоторым другим сопоставимым показателям.

Между индексами всегда имеет место та же зависимость, что и между показателями, которые они выражают: pq = p ∙ q, следовательно, I_pq = I_p ∙ I_q.

Разница между числителем и знаменателем индекса – есть абсолютное изменение явления в целом или его части, которую этот индекс выражает:

Взаимосвязь: pq =p +q =pq_p + pq_q.

Правило построения индекса

В составе любого индекса можно выделить всегда и с любой степенью полноты два фактора – количественный и качественный.

Природа первого очевидна, он поддается непосредственному учету и подсчету

Качественный фактор определяется человеком, исходя из его нужд и потребностей, он не ощущаем органами чувств, его величина определяется в результате тех или иных расчетов.

По методике, принятой в отечественной статистике, при индексировании качественных показателей (цены, себестоимости, производительности труда) количественные берутся в отчётном периоде в числителе и знаменателе индекса, а при индексировании количественных показателей (объёма, трудозатрат) качественные берутся в базисном периоде: ; , .

Такие общие индексы, как правило, называются индексами Пааше. В зарубежной статистике используются индексы Ласпейреса, где показатели фиксируются наоборот.

Агрегатные индексы, имеющие форму средних из индивидуальных(средневзвешенные)

Если нам известны некоторые данные о стоимости товара отчётного и базисного периодов, об изменении цен этих товаров в отчётном году по сравнению с базисным, изменение объёма в отчётном периоде по сравнению с базисным:

Пример. Даны следующие данные ; ; . Найти: ,

Решение:

, ; , ;

; .

Агрегатный индекс переходит в форму средневзвешенного, если в нем используется индивидуальный индекс.

Средневзвешенный индекс качественного фактора, в котором индивидуальный индекс используется как делитель, носит название средневзвешенного гармонического.

Средневзвешенный индекс количественного фактора, в котором индивидуальный индекс используется в качестве сомножителя, называется средневзвешенным арифметическим.

Цепные и базисные индексы

Цепные индексы – отношение любого явления текущего периода к предыдущему: .(; ; )

Базисные индексы – отношение любого явления текущего периода к базисному:

. (; ; )

Индексы постоянного, переменного состава и структурных сдвигов

Индексом постоянного состава называется индекс, рассчитанный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины, причём среднее изменение (изменение всреднем) индексируемой величины (т.е. рассматриваемой части явления):

−общий индекс (цены), индекс постоянного состава или агрегатный индекс (цены), индекс (общий) цены.

Индексом переменного состава называется индекс, характеризующий соотношение средних уровней изучаемого явления в разные периоды времени и показывающий изменение среднего уровня явления (изменений средней цены):

−средней цены; − среднего объёма.

Индекс структурных сдвигов – индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления: .

Между данными индексами существует взаимосвязь: ;

Замечание.

Эти индексы рассчитываются только для одноимённых показателей, если они даны для двух и более объектов за два периода времени, или они могут рассчитываться для нескольких видов товаров на одном предприятии.

Индексы динамики и выполнения плана

−индекс динамики; − индекс выполнения плана.

Классификация индексов по названию

; − индексы товарооборота;

; − индексы затрат на производство;

; − индексы себестоимости;

; − индексы трудоёмкости;

; − индексы физического объёма;

; − индексы цены;

; − индексы производительности труда в трудовой форме;

; − в стоимостной форме, где

i – индивидуальный индекс;

I – общий индекс;

p – цена;

q – физический объём;

t – трудоёмкость;

T – суммарные затраты времени;

w – производительность труда;

z – себестоимость единицы продукции;

zq – затраты на производство;

pq – объём произведённой продукции, товарооборот;

q₀ – физический объём в базисном периоде;

q₁ – физический объём в отчётном периоде.

Индексы сложных экономических явлений

Система взаимосвязанных индексов даёт возможность провести факторный анализ, т.е. определить влияние ряда факторов на изменение результативного показателя (в абсолютном или относительном выражении).

Обозначим через Y объём продукции, произведённой предприятием за год;

через a – среднесписочную численность работников;

через b – среднее число дней, отработанных одним работником за год;

через c – среднюю продолжительность рабочего дня в часах;

через d – среднечасовую выработку одного работника в рублях.

По имеющимся данным составим модель сложного экономического явления, результат которого зависит от нескольких факторов: Y = a ∙ b ∙ c ∙ d.

–этот индекс показывает изменение результативного показателя за счет всех факторов в относительном выражении.

–разница между числителем и знаменателем данного индекса показывает изменение результативного показателя в абсолютном выражении (за счет всех факторов).

Метод цепных подстановок показывает как происходит изменение за счет всех факторов и за счет каждого отдельного фактора.

Относительные изменения (схема обособленного разложения):

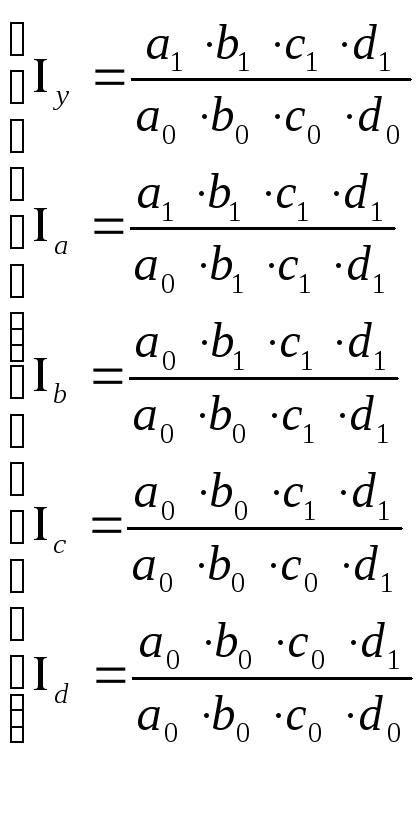
Абсолютные изменения:

Этот метод применяется в экономическом анализе.