Задания, лекции / LAB1

Лабораторная работа N1

Моделирование случайных процессов. Экспериментальная проверка центральной предельной теоремы.

1. Нормальное (гауссовское) распределение.

Это рас­пределение занимает центральное место в теории и практике вероятностно-статистических исследований. В качестве не­прерывной аппроксимации к биномиальному распределению оно впервые рассматривалось А. Муавром еще в 1733 г. (теорема Муавра — Лапласа). Некоторое время спустя нормальное распределение было снова откры­то и изучено независимо друг от друга К. Гауссом (1809 г.) и П. Лапласом (1812 г.). Оба ученых пришли к нормальной функции в связи со своей работой по теории ошибок на­блюдений. Идея их объяснения механизма формирования нормально распределенных случайных величин заключается в следующем. Постулируется, что значения исследуемой непрерывной случайной величины формируются под воз­действием очень большого числа независимых случайных фак­торов, причем сила воздействия каждого отдельного фактора мала и не может превалировать среди остальных, а харак­тер воздействия — аддитивный (т. е. при воздействии слу­чайного фактора F на величину а получается величина a+ (F), где случайная «добавка» (F), мала и равноверо­ятна по знаку ¹ . Можно показать, что функция плотности случайных величин подобного типа имеет вид

(1.1)

где а и,² — параметры закона, интерпретируемые соответ­ственно как среднее значение и дисперсия данной случай­ной величины (в виду особой роли нормального распределе­ния мы будем использовать специальную символику для обозначения его функции плотности и функции распреде­ления).

-----------

1 Строгая теоретическая формализация этих условий содер­жится, например, в центральной предельной теореме Соответствующая функция распределения нормальной случайной величины (а, ²) обозначается Ф(х, а,²) и задается соотношением

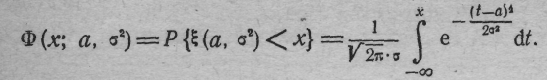(1.1')

Условимся называть нормальный закон с параметрами а=0 и ,²=1 стандартным, а его функции плотности и рас­пределения обозначать соответственно = (x; 0,1) и Ф(х) = Ф(х; 0,1).

Во многих случайных величинах, изучаемых в экономи­ке, технике, медицине, биологии и в других областях, ес­тественно видеть суммарный аддитивный эффект большого числа независимых причин. Но центральное место нормаль­ного закона не следует объяснять его универсальной прило­жимостью, как это было принято долгое время (по-видимому, под влиянием блестящих работ К. Гаусса и П. Лапласа) В этом смысле нормальный закон — это один из многих типов распределения, имеющихся в природе, правда, с от­носительно большим удельным весом практической прило­жимости. И потому нам понятна ирония, звучащая в извест­ном высказывании Липмана (цитируемом А. Пуанкаре в своем труде «Исчисление вероятностей», Париж, 1912 г.): «Каждый уверен в справедливости нормального закона: экспериментаторы — потому, что они думают, что это ма­тематическая теорема; математики — потому, что они ду­мают, что это экспериментальный факт». Однако не следует упускать из виду, что полнота теоретических исследований, относящихся к нормальному закону, а также сравнительно простые математические свойства делают его наиболее при­влекательным и удобным в применении. Даже в случае отклонения исследуемых экспериментальных данных от нормального закона существует по крайней мере два пути его целесообразной эксплуатации: а) использовать его в ка­честве первого приближения; при этом нередко оказывается, что подобное допущение дает достаточно точные с точки зре­ния конкретных целей исследования результаты; б) по­добрать такое преобразование исследуемой случайной ве­личины , которое видоизменяет исходный «не нормальный» закон распределения, превращая его в нормальный. Удоб­ным для статистических приложений является и свойство «самовоспроизводимости» нормального закона, заключаю­щееся в том, что сумма любого числа нормально распреде­ленных случайных величин тоже подчиняется нормальному закону распределения. Кроме того, закон нормального распределения имеет большое теоретическое значение: с его помощью выведен целый ряд других важных распределение построены различные статистические критерии и т. п. (²-, t- и F-распределения и опирающиеся на них критерии.).

Графики нормальных плотностей приведены на рис. 1.1.

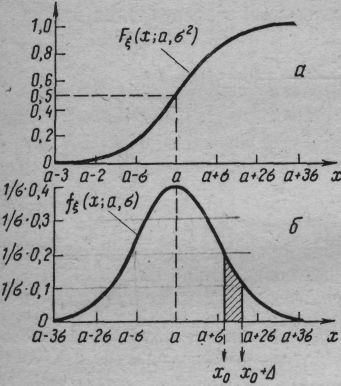
Рис. 1.1. Функции (а) распределения F _норм (x; а, ² ) и f _норм (x; а, ² нормального закона

Основные числовые характеристики нормального закона:

Равномерное (прямоугольное) распределение.

Слу­чайная величина называется равномерно распределенной на отрезке [а,b], если ее плотность вероятности по­стоянна на этом отрезке и равна нулю вне его, т. е.

(1.2)

Так как график функции f (x) изображается в виде прямо­угольника (см. рис.1.1), то такое распределение также на­зывают прямоугольным.

Соответственно функция распределения F (x) равномер­ного закона задается соотношениями:

(1.3)

Примерами реальных ситуаций, связанных с необхо­димостью рассмотрения равномерно распределенных слу­чайных величин, могут служить: анализ ошибок округле­ния при проведении числовых расчетов (такая ошибка, как правило, оказывается равномерно' распределенной на интервале от —5 до +5 -единиц округляемого десятичного знака); время ожидания «обслуживания» при точно перио­дическом, через каждые Т единиц времени, включении

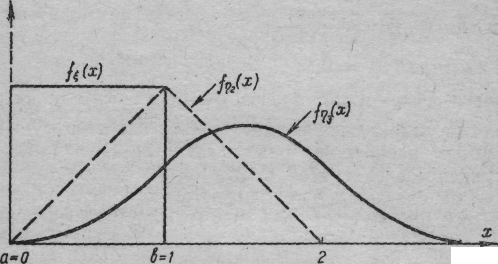
Рис. 1.2. Функция плотности равномерной случайной ве­личины (f(x)) и суммы двух (f(x)) и трех (f(x)) независимых равномерно распределенных на [0, 1] случай­ных величин

(прибытии) «обслуживающего устройства» и при случайном поступлении (прибытии) заявки на обслуживание в этом интервале (например, время ожидания пассажиром прибы­тия поезда метро при условии точных двухминутных ин­тервалов движения метро и случайного момента появле­ния пассажира на платформе будет распределено приблизи­тельно равномерно на интервале [0 мин, 2 мин]).

Отметим еще две важные ситуации, в которых использу­ется равномерный закон. Во-первых, в теории и практике статистического анализа данных широко используется вспо­могательный переход от исследуемой случайной величины с функцией распределения F(x) к случайной величине =F(), которая оказывается равномерно распределенной на отрезке. Этот прием является полезным при статистическом моделировании наблюдений, подчинен­ных заданному закону распределения вероятностей, при построении доверительных границ для иссле­дуемой функции распределения и, в ряде других задач математической статистики. Во-вторых, равномерное распределение иногда используется в качестве «нулевого прибли­жения» в описании априорного распределения анализи­руемых параметров в так называемом байесовском подходе в условиях полного отсутствия априорной информации об этом распределении.

Числовые характеристики равномерного закона:

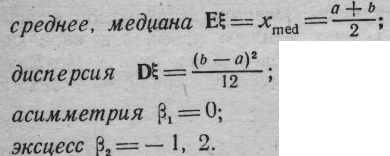
Отметим в заключение одно важное свойство суммы n независимых равномерно распределенных случайных ве­личин: распределение этой суммы очень быстро (по мере роста числа слагаемых) приближается к нормальному за­кону. В частности, если _i— равномерно распределенные на отрезке [0,1] и независимые случайные величины, то можно показать, что плотность такой случайной величины имеет вид

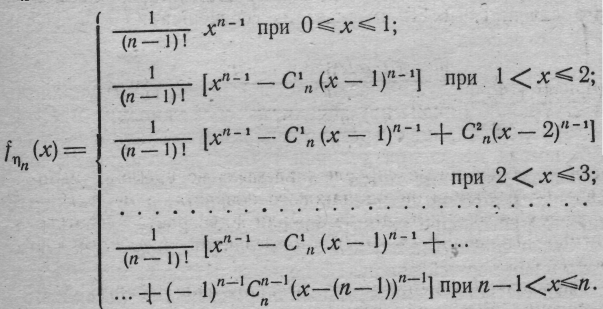
(область возможных значений случайной величины _n оче­видно, задается отрезком [0, n]). Геометрическое изображе­ние последовательного изменения вида плотности f_n по мере роста числа слагаемых n (для n = 1,2, 3) дано на рис. 1.2. Это свойство используется, в частности, при статис­тическом моделировании нормально распределенных на­блюдений.

3. Проверка соответствия выбранной моделираспределения исходным данным (критерии согласия)

Пусть нами высказано предположение, что ряд наблюдений (1.1) образует случайную выборку, извлеченную из гене­ральной совокупности с некоторой модельной функцией распределения F_mod(X; ⁽¹⁾, ..., ^(s)) где общий вид функции F_mod (т. е. тип модели) считается известным, а параметры, от которых она зависит, могут быть как известными, так и неизвестными.

Описываемые в данном параграфе критерии согласия предназначены для проверки гипотезы

H₀ : F(x)= F_mod(X; ⁽¹⁾, ..., ^(s)) (3.2)

и основаны на использовании различных мер расстоянии между анализируемой эмпирической функцией распределения, определяемой по выборке и гипотетической модельной F_mod(x; ⁽¹⁾, ..., ^(s)).

3.1. Критерий ² Пирсона. Данный критерий согласия позво­ляет осуществлять проверку гипотезы (3.2) в условиях, когда значения параметров ⁽¹⁾, ..., ^(s)модельной функции распределения не известны исследователю. Для измерения степени отклонения эмпирического распределения от мо­дельного этот критерий использует статистику ² (читается хи-квадрат) Процедура статисти­ческой проверки гипотезы (3.2) складывается в данном случае из следующих этапов.

1. Весь диапазон значений исследуемой случайной ве­личины разбивается на ряд интервалов группирования ₁, ₂,…, _k не обязательно одинаковой длины. Это раз­биение на интервалы необходимо подчинить следующим условиям:

а) общее количество интервалов k должно быть не мень­шим 8;

б) в каждый интервал группирования, должно попасть не менее 7—10 выборочных значений , причем желательно, чтобы в разные интервалы попало примерно одинаковое число точек;

в) если диапазон исследуемой случайной величины — вся числовая прямая (полупрямая), то крайние интервалы группирования будут полупрямыми (соответственно один из них).

2. На основании выборочных данных х₁, x₂, … x_n cтро­ятся статистические оценки неизвестных параметров, от которых зависит данный закон распределения F. Более корректным способом действий считается тот, при котором оценки вычисляются на основе сгруппиро­ванных данных.

3. Подсчитываются числа v_i точек, попавших в каждый из интервалов группирования _i , и вычисляются вероят­ности событий _i т. е. вероятности

попадания в те же интервалы _i;

4. Вычисляется величина критической статистики ² (k—s—1) по формуле

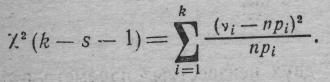
Далее находятся 100(1—/2) %-ная точка ²_1-/2 (k—s—1) и 100 /2 %-ная точка ²_/2 (k—s—1) ² распределения с k—s—1 степенями свободы (, как обычно, уровень значимости, которым мы задаемся заранее). Если

то гипотеза, о том, что исследуемая случайная величина | действительно подчиняется закону распределения F_mod, принимается.

3.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям, Для при­ближенной проверки нормальности исследуемой случай­ной величины по результатам ее наблюдения х₁, x₂, … x_n можно воспользоваться некоторыми характерными свойст­вами нормального распределения. В частности, как извест­но, в случае нормального распределения характеристики асимметрии ₁ и эксцесса ₂) должны быть нулевыми и .

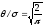Поскольку практически мы имеем дело лишь с приближенными, выборочными значениями асимметрии эксцесса, средних абсолютного и квадратического отклонений, то мы не можем требовать точного выполнения соотношений

₁ = ₂ =0.

d_n = _n/s(n) = (3.3)

Однако исходя из нормального характера распределения исследуемой случайной величины , можно вывести и затабулировать законы распределения для ₁(n), ₂(n), (или для некоторых, подходящих для наших целей их комбина­ций) и тем самым определить степень «допустимых» (в пре­делах нормальности ) отклонений от (3.3). Рассмотрим вариант приближенной проверки нормаль­ности, основанной на вышеупомянутых свойствах ₁,

1. Для проверки нормального характера распределения по асимметрии ₁(n), и отношению средних отклонений d_n = _n/s(n) в случае сравнительно небольших объемов выборок (n>25) целесообразно воспользоваться наличием таблиц для вычисления (по данным входным параметрам Q и n) точных значений 100Q%-ных точек распределения статистик ₁(n), и d_n. В частности, процедура проверки нормаль­ности в данном случае будет следующей: по формуле находим ₁(n) – асимметрию:

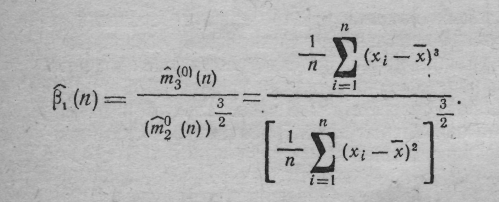
Далее подсчитываем величину d_n .

Задавшись для Q₁ одним из значений 0,01 или 0,05 и при­нимая во внимание объем выборки n по табл. находим величину 100 %-ной точки _1.Q1 задавшись для Q₂ одним из значений 0,01, 0,05 или 0,10 и принимая во внимание объем выборки n, по табл. из [*] находим величины 100(1-Q₂)%- ной точки d _{n Q2} и 100(1—Q₂) %-ной точки d_n•1-Q2 если хотя бы одно из неравенств

оказалось нарушенным, то гипотеза нормальности отвер­гается с уровнем значимости , подчиняющимся неравенствам 1:

2max (Q₁, Q₂)< < 2 (Q₁, + Q₂) - 2Q₁Q₂.

Существует также ряд других способов проверки нормального характера распределения по асимметрии, эксцессу.

* Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. М.Наука., 1985.

4. Задания

В данной лабораторной работе моделирование производится посредством табличного процессора MS Excel.

1. Смоделировать пятнадцать измерений случайной величины X(n=15), имеющей равномерный закон распределения на отрезке [0,1]. Представить измерения в виде вертикально расположенного массива.

Для этого можно, например, ввести n произвольных значений, примерно соблюдая закон распределения (т.е. с примерно равномерным распределением значений от 0 до 1). Можно воспользоваться функцией СЛЧИС (случайное число).

2. Найти среднее значение, среднеквадратичное отклонение, выборочную асимметрию, эксцесс. Разбить отрезок [0,1] на интервалы с учетом рекомендаций в разделе 3.1. , найти частоты, построить гистограмму.

Сделать предварительные выводы о характере распределения.

Замечания:

Для вычисления оценок основных статистических характеристик можно использовать соответствующие встроенные функции.

Для нахождения частот можно использовать функцию ЧАСТОТА. При этом следует иметь ввиду, что функция данная функция возвращает массив, поэтому для вывода значений можно воспользоваться функцией ИНДЕКС. (Рекомендуется посмотреть справочные данные по этим функциям и отработать тестовые примеры).

Желательно характеристики снабжать надписями и обозначениями, данные располагать удобно, наглядно, с определенной системой (например, значения в столбик, характеристики под ними и т.д….)

3. Смоделировать еще одну переменную Y(n=15), имеющей равномерный закон распределения на отрезке [0,1]. Для нее повторить задания п. 1 и 2.

4. Найти значения переменной Z, представляющей сумму соответствующих двух переменных ( z_i=x_i+y_i) Для нее повторить задания п. 1 и 2. Сделать предварительные выводы о характере распределения. При выборе интервалов следует иметь ввиду, что отрезок, которому будут принадлежать значения уже окажется [0,2].

5) Повторить эксперимент для суммы трех равномерно распределенных величин (теперь отрезок будет [0,3]. Дополнительно, проверить гипотезу о нормальном характере распределения по критерию Пирсона.

При этом рекомендуется на свободном месте построить таблицу, содержащую следующие столбцы:

1. левый конец интервала,

2. правый конец интервала,

3. частоты v_i ,

4. значение модельного распределения на левом конце интервала,

5. значение модельного распределения на правом конце интервала,

6. вероятность попадания в интервал p_i (разность 2 и 3),

7. .

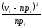число строк - число интервалов.

Далее согласно 3.1 найти критерий и произвести проверку гипотезы. Для нахождения процентных точек можно воспользоваться функцией XИ2ОБР.

Замечание: имеющаяся в арсенале процедура ПИРСОН рассчитывает коэффициент корреляции и не относится к данному критерию согласия.

6.) Проделать эксперимент 5 для сумм 5-и и 12-и равномерно распределенных величин. Для данных случаев (кроме первого раза) можно использовать функцию XИ2ТЕСТ. Попытаться примерно оценить гипотезу о нормальном распределении с учетом п. 3.2 теоретической части.

7) Повторить эксперименты при n=50. Сделать выводы.