.Выборочная дисперсия.

Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения , вводят сводную характеристику- выборочную дисперсию.

Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения признака выборки различны, то

если же все значения имеют частоты n1, n2,…,nk, то

Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.

Выборочным средним квадратическим отклоненим называют квадратный корень из выборочной дисперсии:

Вычисление дисперсии- выборочной или генеральной, можно упростить, используя формулу:

Замечание: если выборка представлена интервальным вариационным рядом, то за xi принимают середины частичных интервалов.

11) Гистограмма, столбчатая диаграмма, один из видов графического изображения статистического распределении каких-либо величин по количественному признаку. Г. представляет собой совокупность смежных прямоугольников, построенных на прямой линии. Площадь каждого прямоугольника пропорциональна частоте нахождения данной величины в изучаемой совокупности. Пусть, например, измерение диаметров стволов 624 сосен дало следующие результаты:

Диаметр, см 14—22,22—30,30—38,38—62Число стволов57,232,212,123.На горизонтальной оси откладываются границы групп, на которые стволы разбиты по их диаметру, и на отрезке, соответствующем каждой группе, строится как на основании прямоугольник с площадью, пропорциональной числу стволов, попавших в данную группу

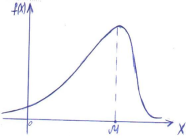
Модой случайной величины называется её наиболее вероятное значение. Термин «наиболее вероятное значение», строго говоря, применим только к прерывным величинам; для непрерывной величины модой является то значение, в котором плотность вероятности максимальна. На рис. А и Б показана мода соответственно для прерывной и непрерывной случайных величин.

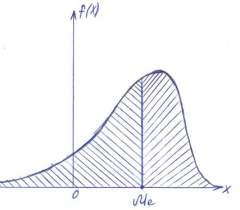
Часто применяется еще одна характеристика положения – так называемая медиана случайной величины. Этой характеристикой пользуются обычно только для непрерывных случайных величин, хотя формально можно её определить и для прерывной величины. Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.

Если все значения признака выборки различны, то

Если же все значения имеют частоты n1, n2,…,nk, то

12)Прямые измерения-числовые значения искомой величины получаются сравнением её с мерой(температура,длина,расстояние).

Косвенные-сводятся к нахождению значения искомой величины по известной зависимости между нею и измеренными величинами.

Погрешность-количественная х-ка качества измерения.

Абсолютная погрешность(дельта х)-разность между результатом измерения и истиным значением измеряемой величины.

дельта х=х-х0.

Относит.погрешность(Е)

Е=дельта х/х0*100%

Систематич. погрешности сохраняют постоянное значение или изменяются по известному закону в ходе измерения.

Пример:уличный термометр(дельта х=3 градусаС)

Чаще всего к систематич. относят приборные погрешности(инструментальные).Они обусловлены особенностью самого измерит. средства и его характеристиками(цена деления прибора).

Грубые погрешности(промахи)-возникают при резких изменениях условий измерений или ошибках самого оператора.(дельта t=1 час)

Пример:37.1,37.0,39.9,36.9,37.1

Результат грубой погрешности приводит к резкому отличию данных.

Случ. погр.-имеются при всех измерениях и явл. следствием случ. статических процессов в измерительном средстве или объекте измерения. Проявляются только тогда,когда измерит. средства обеспеч. достаточно высокую точность.Они имеют случайные по величине и знаку значения.

13)