Учитывая выражение (10), модуль упругости воздуха представим в виде

.

Будем считать изменения давления и объема бесконечно малым и учтем, что увеличению давления соответствует уменьшение объема:

. (11)

Сжатие и разрежение воздуха сопровождается изменением его температуры. При быстрых сжатиях и разрежениях температуры отдельных участков воздуха не успевают выравниваться за время одного колебания. Поэтому процессы сжатия и разрежения в звуковой волне можно считать происходящими без теплообмена, т.е. адиабатическими, описываемыми уравнением Пуассона

, (12)

где γ  C_p/C_V, причем C_p- теплоемкость воздуха при постоянном давлении, а C_V – теплоемкость при постоянном объеме.

Определим отношение dp/dV, входящее в выражение (11), из уравнения Пуассона. Для этого продифференцируем (12):

откуда

. (13)

Подставляя выражение (13) в формулу (11), получим

Е  γp. (14)

Плотность воздуха ρ, входящая в уравнение (9), может быть выражена из уравнения Менделеева-Клапейрона

,

откуда

, (15)

где Т – температура, R  8,31Дж/(мольК) – универсальная газовая постоянная, μ- молярная масса газа воздуха.

Подставляем выражение (14) и (15) в формулу (8), получим

. (16)

Зная скорость звука в воздухе и его температуру, можно из выражения (16) найти отношение теплоемкостей .

Стоячие волны.Из опыта вытекает следующее утверждение, называемое принципом суперпозиции: если в среде распространяется несколько волн, то колебания каждой частицы среды оказываются геометрической суммой колебаний, вызываемых каждой из волн в отдельности.

Волны называются когерентными, если они имеют постоянную разность фаз.

При наложении когерентных волн друг на друга наблюдается интерференция. Это явление состоит в том, что колебания в одних точках среды усиливают, а в других ослабляют друг друга, причем эта картина неизменна во времени.

Колебательный процесс, возникающий при наличии двух встречных волн с одинаковой амплитудой, называется стоячей волной. Стоячие волны образуются при отражении волн от преграды, когда складываются падающая на преграду волна и бегущая ей навстречу отраженная.

Получим уравнение стоячей волны. Для этого сложим уравнения двух плоских волн, распространяющихся вдоль оси Хв противоположных направлениях. Эти уравнения должны различаться знаком проекции вектора скорости волны на осьХ(или знаком волнового числаk):

,

.

Преобразовав результат сложения этих уравнений по формуле для суммы косинусов, получим

.

Если подставить вместо k значение 2π/λ, то уравнение примет вид

. (17)

Уравнение (17) представляет собой уравнение стоячей волны. Из него видно, что частота колебаний стоячей волны та же, что и у исходных встречных волн. Амплитуда волны зависит от xи равна

.

Амплитуда обращается в нуль при значениях x_узл, удовлетворяющих условию

при (n  0,1,2,…). (18)

В точках пространства с такими координатами частицы среды остаются неподвижными, и эти точки называются узлами стоячей волны.

Точки пространства, в которых частицы среды колеблются с максимальной амплитудой, называются пучностямистоячей волны. Их положение в пространстве характеризуется координатамиx_пчн, определяемыми из условия

при (n  0,1,2,…). (19)

Из формул (18) и (19) следует, что расстояние между соседними пучностями, так же как и расстояние между соседними узлами, равно половине длины волны λ/2. Пучности и узлы сдвинуты друг относительно друга на четверть длины волны.

Множитель в уравнении (17) при переходе через нуль меняет знак. Следовательно, фаза колебаний по разные стороны от узла отличается на, т.е. точки, лежащие по разные стороны от узла, колеблются в противофазе. Все точки, заключенные между двумя соседними узлами, колеблются в одной и той же фазе (синфазно). График стоячей волны показан на рис.6.

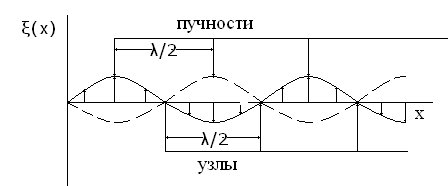
Рис.6.

Экспериментальная установка

В данной работе скорость звука определяется методом стоячих волн. Если вдоль стоячей волны перемещать приемник звука, то можно заметить периодическое изменение громкости звука, обусловленное чередованием узлов и пучностей стоячей волны. Такой же результат можно получить, если приемник звука оставить неподвижным, а перемещать границу раздела двух сред, от которой отражается падающая волна.

Схема установки, используемой в данной работе, показана на рис.7.

Установка работает следующим образом. Генератор 1 вырабатывает переменное электрическое напряжение звуковой частоты. Это напряжение, подается на катушку телефона 2 и преобразуется в звуковые колебания мембраны. Звуковые волны распространяются по воздушному столбу в трубе 3 и отражаются от поршня. При взаимодействии падающей и отраженной волны образуется стоячая волна. Перемещая поршень 4 вдоль трубы можно добиться максимального звучания воздушного столба, соответствующего стоячей волне с максимальной амплитудой в зоне расположения поршня. Положение поршня в этот момент можно определить по линейке 5. Дальнейшее изменение положения поршня вызовет последовательную смену узлов и пучности стоячей волны.

Так как расстояние между пучностями стоячей волны равно половине длины волны, то длина волны равна удвоенной разности отсчетов между двумя ближайшими максимумами звука:

  2(h_i  h_i-1).

Частота звуковых колебаний ν генератора определяется по его шкале. Зная длину звуковой волны λ и частоту ν, можно определить скорость распространения звука по формуле

V_в  λν. (20)