2. Способы представления синусоидальных токов, напряжений и эдс. Аналитический способ Аналитический способ

Для тока

(2.1)

i(t) = I_m sin(ωt + ψ_i),

для напряжения

(2.2)

u(t) = U_m sin (ωt +ψ_u),

для ЭДС

(2.3)

e(t) = E_m sin (ωt +ψ_e),

В уравнениях (2.1 – 2.3) обозначено:

I_m, U_m, E_m – амплитуды тока, напряжения, ЭДС; значение в скобках – фаза (полная фаза); ψ_i, ψ_u, ψ_e – начальная фаза тока, напряжения, ЭДС; ω – циклическая частота, ω = 2πf; f – частота, f = 1 / T; Т – период.

Величины i, I_m – измеряются в амперах, величины U, U_m, e, E_m – в вольтах; величина Т (период) измеряется в секундах (с); частота f – в герцах (Гц), циклическая частота ω имеет размерность рад/с. Значения начальных фаз ψ_i, ψ_u, ψ_e могут измеряться в радианах или градусах. Величина ψ_i, ψ_u, ψ_e зависит от начала отсчета времени t = 0. Положительное значение откладывается влево, отрицательное – вправо.

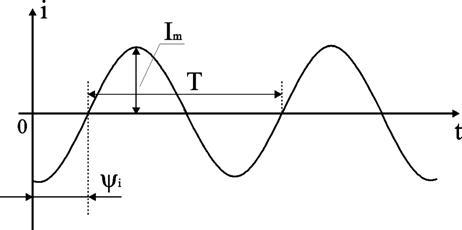
Временная диаграмма

Временная диаграмма представляет графическое изображение синусоидальной величины в заданном масштабе в зависимости от времени (рис. 2.1).

i(t) = I_m sin(ωt - ψ_i).

Графоаналитический способ

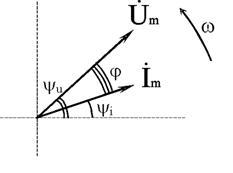Рис. 2.2

Графически синусоидальные величины изображаются в виде вращающегося вектора (рис. 2.2). Предполагается вращение против часовой стрелки с частотой вращения ω. Величина вектора в заданном масштабе представляет амплитудное значение. Проекция на вертикальную ось есть мгновенное значение величины.

Совокупность векторов, изображающих синусоидальные величины (ток, напряжение, ЭДС) одной и той же частоты называют векторной диаграммой.

Векторные величины отмечаются точкой над соответствующими переменными.

Использование векторных диаграмм позволяет существенно упросить анализ цепей переменного тока, сделать его простым и наглядным.

В основе графоаналитического способа анализа цепей переменного тока лежит построение векторных диаграмм.

Аналитический метод с использованием комплексных чисел

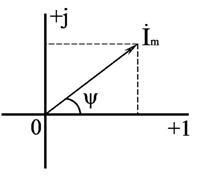Рис. 2.5

Синусоидальный ток i(t) = I_m sin(ωt + ψ) можно представить комплексным числом Í_m на комплексной плоскости (рис. 2.5)

Í_m = I_me^jψ,

где амплитуда тока I_m – модуль, а угол ψ, являющийся начальной фазой, – аргумент комплексного тока.

Использование комплексной формы представления позволяет заменить геометрические операции над векторами алгебраическими операциями над комплексными числами. В результате этого к анализу цепей переменного тока могут быть применены все методы анализа цепей постоянного тока.

Билет №18

1. Резонанс тока.

Резонанс токов возникает в цепях переменного тока состоящих из источника колебаний и параллельного колебательного контура. Резонанс тока это увеличение тока проходящего через элементы контура при этом увеличение потребление тока от источника не происходит.

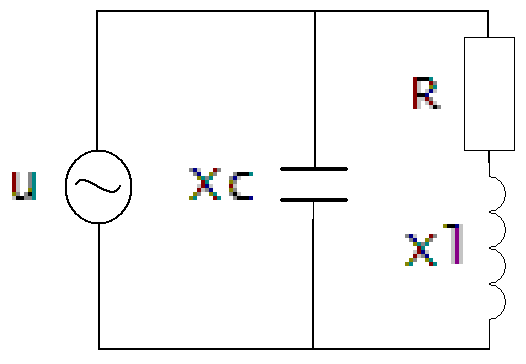
Рисунок 1 — параллельный колебательный контур

 

 Для возникновения резонанса токов необходимо чтобы реактивные сопротивления емкости и индуктивности контура были равны. А также частота собственных колебаний контура была равна частоте колебаний источника тока.  Во время наступления резонанса токов или так называемого параллельного резонанса напряжение на элементах контура остается неизменным и равным напряжению, которое создает источник. Поскольку он подключен параллельно контуру. Потребление тока от источника будет минимально, так как сопротивление контура при наступлении резонанса резко увеличится.

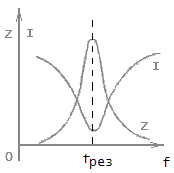
Рисунок 2 — зависимость полного сопротивления контура и тока от частоты

 

 Сопротивление колебательного контура относительно источника колебаний будет иметь чисто активный характер. То есть не будет, провялятся ни емкостная, ни индуктивная составляющая. И сдвиг фаз между током и напряжением будет отсутствовать.  В тоже время ток через индуктивность будет отставать от напряжения  на 90 градусов. А ток в емкости буде опережать напряжение на те же 90 градусов. Таким образом, токи в реактивных элементах контура будут сдвинуты по фазе на 180 градусов друг относительно друга.  В итоге получается, что в параллельном колебательном контуре протекают реактивные токи достаточно большой величины, но при этом он от источника напряжения потребляет малый ток необходимый лишь для  компенсации потерь в контуре. Эти потери обусловлены наличием активного сопротивления сосредоточенного по большей части в индуктивности.  Источник затрачивает энергию при включении, заряжая емкость. Далее энергия, накопленная в электрическом поле конденсатора, переходит в энергию магнитного поля индуктивности. Индуктивность возвращает энергию емкости, и процесс повторяется снова. Источник напряжения лишь должен компенсировать потери энергии в активном сопротивлении контура.

2. Расчёт эквивалентного сопротивления электрической цепи.

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

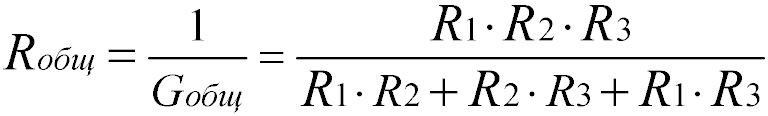
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.