Вопросы - Ответы Программирование

сравнить все остальные элементы с опорным, на основании сравнения разбить множество на три — «меньшие опорного», «равные» и «большие», расположить их в порядке меньшие-равные-большие.

повторить рекурсивно для «меньших» и «больших».

Алгоритм

Быстрая сортировка использует стратегию «разделяй и властвуй». Шаги алгоритма таковы:

1.Выбираем в массиве некоторый элемент, который будем называть опорным элементом. С точки зрения корректности алгоритма выбор опорного элемента безразличен. С точки зрения повышения эффективности алгоритма выбираться должна медиана, но без дополнительных сведений о сортируемых данных еѐ обычно невозможно получить. Известные стратегии: выбирать постоянно один и тот же элемент, например, средний или последний по положению; выбирать элемент со случайно выбранным индексом.

2.Операция разделения массива: реорганизуем массив таким образом, чтобы все элементы, меньшие или равные опорному элементу, оказались слева от него, а все элементы, большие опорного — справа от него. Обычный алгоритм операции:

1.Два индекса — l и r, приравниваются к минимальному и максимальному индексу разделяемого массива соответственно.

2.Вычисляется индекс опорного элемента m.

3.Индекс l последовательно увеличивается до m до тех пор, пока l-й элемент не превысит опорный.

4.Индекс r последовательно уменьшается до m до тех пор, пока r-й элемент не окажется меньше либо равен опорному.

5.Если r = l — найдена середина массива — операция разделения закончена, оба индекса указывают на опорный элемент.

6.Если l < r — найденную пару элементов нужно обменять местами и продолжить операцию разделения с тех значений l и r, которые были достигнуты. Следует учесть, что если какая-либо граница (l или r) дошла до опорного элемента, то при обмене значение m изменяется на r-й или l-й элемент соответственно.

3.Рекурсивно упорядочиваем подмассивы, лежащие слева и справа от опорного элемента.

4.Базой рекурсии являются наборы, состоящие из одного или двух элементов. Первый возвращается в исходном виде, во втором, при необходимости, сортировка сводится к перестановке двух элементов. Все такие отрезки уже упорядочены в процессе разделения.

Поскольку в каждой итерации (на каждом следующем уровне рекурсии) длина обрабатываемого отрезка массива уменьшается, по меньшей мере, на единицу, терминальная ветвь рекурсии будет достигнута всегда и обработка гарантированно завершится.

Интересно, что Хоар разработал этот метод применительно к машинному переводу: дело в том, что в то время словарь хранился на магнитной ленте, и если упорядочить все слова в тексте, их переводы можно получить за один прогон ленты.

Оценка эффективности

QuickSort является существенно улучшенным вариантом алгоритма сортировки с помощью прямого обмена (его варианты известны как «Пузырьковая сортировка» и «Шейкерная сортировка»), известного, в том числе, своей низкой эффективностью. Принципиальное отличие состоит в том, что в первую очередь меняются местами наиболее удалѐнные друг от друга элементы массива. Любопытный факт: улучшение самого неэффективного прямого метода сортировки дало в результате самый эффективный улучшенный метод.

Лучший случай. Для этого алгоритма самый лучший случай — если в каждой итерации каждый из подмассивов делился бы на два равных по величине массива. В результате количество сравнений, делаемых быстрой сортировкой, было бы

равно значению рекурсивного выражения CN = 2CN/2+N. Это дало бы наименьшее время сортировки.

Среднее. Даѐт в среднем O(n lg n) обменов при упорядочении n элементов. В реальности именно такая ситуация обычно имеет место при случайном порядке элементов и выборе опорного элемента из середины массива либо случайно. На практике быстрая сортировка значительно быстрее, чем другие алгоритмы с

оценкой O(n lg n), по причине того, что внутренний цикл алгоритма может быть

эффективно реализован почти на любой архитектуре. 2CN/2 покрывает расходы по сортировке двух полученных подмассивов; N — это стоимость обработки каждого элемента, используя один или другой указатель. Известно также, что примерное значение этого выражения равно CN = N lg N.

Худший случай. Худшим случаем, очевидно, будет такой, при котором на каждом этапе массив будет разделяться на вырожденный подмассив из одного опорного элемента и на подмассив из всех остальных элементов. Такое может произойти, если в качестве опорного на каждом этапе будет выбран элемент либо наименьший, либо наибольший из всех обрабатываемых.

Худший случай даѐт O(n²) обменов, но количество обменов и, соответственно, время работы — это не самый большой его недостаток. Хуже то, что в таком случае глубина рекурсии при выполнении алгоритма достигнет n, что будет означать n-кратное сохранение адреса возврата и локальных переменных процедуры разделения массивов. Для больших значений n худший случай может привести к исчерпанию памяти во время работы алгоритма. Впрочем, на большинстве реальных данных можно найти решения, которые минимизируют вероятность того, что понадобится квадратичное время.

Улучшения

При выборе опорного элемента из данного диапазона случайным образом худший случай становится очень маловероятным и ожидаемое время выполнения алгоритма сортировки — O(n lg n).

Во избежание достижения опасной глубины рекурсии в худшем случае (или при приближении к нему) возможна модификация алгоритма, устраняющая одну ветвь рекурсии: вместо того, чтобы после разделения массива вызывать рекурсивно процедуру разделения для обоих найденных подмассивов, рекурсивный вызов делается только для меньшего подмассива, а больший обрабатывается в цикле в пределах этого же вызова процедуры. С точки зрения эффективности в среднем случае разницы практически нет: накладные расходы на дополнительный рекурсивный вызов и на организацию сравнения длин подмассивов и цикла — примерно одного порядка. Зато глубина рекурсии ни при каких обстоятельствах не

превысит log2n, а в худшем случае она вообще будет не более 2 — вся обработка пройдѐт в цикле первого уровня рекурсии.

Достоинства и недостатки

Достоинства:

Один из самых быстродействующих (на практике) из алгоритмов внутренней сортировки общего назначения.

Прост в реализации.

Требует лишь O(lgn) дополнительной памяти для своей работы.

Хорошо сочетается с механизмами кэширования и виртуальной памяти.

Существует эффективная модификация (алгоритм Седжвика) для сортировки строк — сначала сравнение с опорным элементом только по нулевому символу строки, далее применение аналогичной сортировки для «большего» и «меньшего» массивов тоже по нулевому символу, и для «равного» массива по уже первому символу.

Недостатки:

Сильно деградирует по скорости (до Θ(n2)) при неудачных выборах опорных элементов, что может случиться при неудачных входных данных. Этого можно избежать, используя такие модификации алгоритма, как Introsort, или вероятностно, выбирая опорный элемент случайно, а не фиксированным образом.

Наивная реализация алгоритма может привести к ошибке переполнения стека, так как ей может потребоваться сделать O(n) вложенных рекурсивных вызовов. В улучшенных реализациях, в которых рекурсивный вызов происходит только для

сортировки бо́льшей из двух частей массива, глубина рекурсии гарантированно не превысит O(lgn).

Неустойчив — если требуется устойчивость, приходится расширять ключ.

Сортировка слиянием также построена на принципе "разделяй-и-властвуй", однако реализует его несколько по-другому, нежели quickSort. А именно, вместо разделения по опорному элементу массив просто делится пополам.

// a - сортируемый массив, его левая граница lb, правая граница ub template<class T>

Функция merge на месте двух упорядоченных массивов a[lb]...a[split] и a[split+1]...a[ub] создает единый упорядоченный массив a[lb]...a[ub].

Пример работы алгоритма на массиве 3 7 8 2 4 6 1 5..

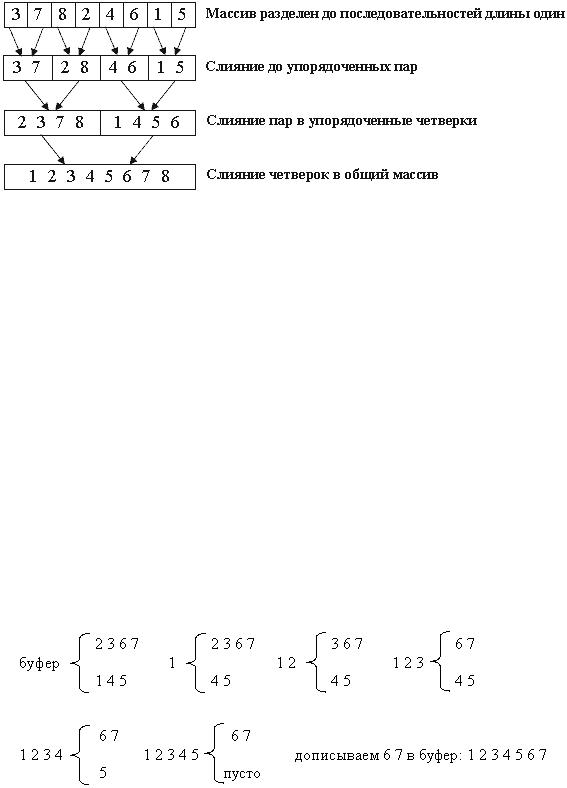
Рекурсивный алгоритм обходит получившееся дерево слияния в прямом порядке. Каждый уровень представляет собой проход сортировки слияния - операцию, полностью переписывающую массив.

Обратим внимание, что деление происходит до массива из единственного элемента. Такой массив можно считать упорядоченным, а значит, задача сводится к написанию функции слияния merge.

Один из способов состоит в слиянии двух упорядоченных последовательностей при помощи вспомогательного буфера, равного по размеру общему количеству имеющихся в них элементов. Элементы последовательностей будут перемещаться в этот буфер по одному за шаг.

merge ( упорядоченные последовательности A, B , буфер C ) { пока A и B непусты {

cравнить первые элементы A и B переместить наименьший в буфер

}

если в одной из последовательностей еще есть элементы дописать их в конец буфера, сохраняя имеющийся порядок

}

Пример работы на последовательностях 2 3 6 7 и 1 4 5

Результатом является упорядоченная последовательность, находящаяся в буфере. Каждая операция слияния требует n пересылок и n сравнений, где n - общее число элементов, так что время слияния: Theta(n).

template<class T>

void merge(T a[], long lb, long split, long ub) {

//Слияние упорядоченных частей массива в буфер temp

//с дальнейшим переносом содержимого temp в a[lb]...a[ub]

//текущая позиция чтения из первой последовательности a[lb]...a[split] long pos1=lb;

//текущая позиция чтения из второй последовательности a[split+1]...a[ub] long pos2=split+1;

//текущая позиция записи в temp

long pos3=0;

T *temp = new T[ub-lb+1];

//идет слияние, пока есть хоть один элемент в каждой последовательности while (pos1 <= split && pos2 <= ub) {

if (a[pos1] < a[pos2]) temp[pos3++] = a[pos1++];

else

temp[pos3++] = a[pos2++];

}

//одна последовательность закончилась -

//копировать остаток другой в конец буфера

// скопировать буфер temp в a[lb]...a[ub] for (pos3 = 0; pos3 < ub-lb+1; pos3++)

a[lb+pos3] = temp[pos3];

delete temp[ub-lb+1];

}

Оценим быстродействие алгоритма: время работы определяется рекурсивной формулой

T(n) = 2T(n/2) + Theta(n).

Ее решение: T(n) = n log n - результат весьма неплох, учитывая отсутствие "худшего случая". Однако, несмотря на хорошее общее быстродействие, у сортировки слиянием есть и серьезный минус: она требует Theta(n) памяти.

Хорошо запрограммированная внутренняя сортировка слиянием работает немного быстрее пирамидальной, но медленнее быстрой, при этом требуя много памяти под буфер. Поэтому mergeSort используют для упорядочения массивов, лишь если требуется устойчивость метода(которой нет ни у быстрой, ни у пирамидальной сортировок).

Сортировка слиянием является одним из наиболее эффективных методов для односвязных списков и файлов, когда есть лишь последовательный доступ к элементам.

9. Алгоритмы поиска.

Двоичный (бинарный) поиск (также известен как метод деления пополам и дихотомия) — классический алгоритм поиска элемента в отсортированном массиве (векторе). Используется в информатике, вычислительной математике и математическом программировании.

Поиск элемента отсортированного массива

Для поиска элемента x массива A, отсортированного в возрастающем порядке, применяется следующий алгоритм:

i := 0; { индекс перед первым элементом массива }

j := n + 1; { индекс после последнего элемента массива }

while i < j - 1 do begin

{ ищем элемент на интервале индексов от i до j, не включая i и j } k := (i + j) div 2; { k = элемент посередине интервала }

if x >= A[k] then i := k

else

j := k;

end;

if (i > 0) and (A[i] = x) then begin

{ элемент найден } end;

{

1) при каждой итерации цикла поддерживается инвариант: A[i] <= x и A[j] >

x.

2)остановится, когда i = j - 1. можно понять, что к 0 и (n + 1)-ому элементу никогда не обратится

3)очень удобная реализация бинпоиска, когда дана функция, которая делит отрезок на две части, где первая удовлетворяет предикату, а вторая нет, и причем бинпоиск находит два таких соседних

элемента, из которых только один удовлетворяет.

}

Стоит отметить, что в виду возможного арифметического переполнения при работе с

массивами большого размера, индекс элемента посередине интервала [i, j] следует считать не по формуле (i + j) div 2, а как i + (j - i) div 2.[1]

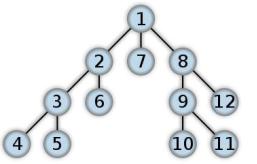
Двоичное дерево поиска (англ. binary search tree, BST) — это двоичное дерево, для

которого выполняются следующие дополнительные условия (свойства дерева поиска):

Оба поддерева — левое и правое, являются двоичными деревьями поиска.

У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных узла X.

У всех узлов правого поддерева произвольного узла X значения ключей данных не меньше, нежели значение ключа данных узла X.

Очевидно, данные в каждом узле должны обладать ключами на которых определена операция сравнения меньше.

Как правило, информация, представляющая каждый узел, является записью, а не единственным полем данных. Однако, это касается реализации, а не природы двоичного дерева поиска.

Для целей реализации двоичное дерево поиска можно определить так:

Двоичное дерево состоит из узлов (вершин) — записей вида (data, left, right), где data — некоторые данные привязанные к узлу, left и right — ссылки на узлы, являющиеся детьми данного узла - левый и правый сыновья соответственно. Для оптимизации алгоритмов конкретные реализации предполагают также, определения в каждом узле кроме корневого поля parent - ссылки на родительский элемент.

Данные (data) обладают ключом (key) на котором определена операция сравнения "меньше". В конкретных реализациях это может быть пара (key, value) - (ключ и значение), или ссылка на такую пару, или простое определение операции сравнения на необходимой структуре данных или ссылке на неё.

Для любого узла X выполняются свойства дерева поиска: key*left*X++ < key*X+ ≤ key*right*X++, т. е. ключи данных родительского узла больше ключей данных левого сына и нестрого меньше ключей данных правого.

Двоичное дерево поиска не следует путать с двоичной кучей, построенной по другим правилам.

Основным преимуществом двоичного дерева поиска перед другими структурами данных является возможная высокая эффективность реализации основанных на нѐм алгоритмов поиска и сортировки.

Двоичное дерево поиска применяется для построения более абстрактных структур, таких как множества, мультимножества, ассоциативные массивы.

Основные операции в двоичном дереве поиска

Базовый интерфейс двоичного дерева поиска состоит из трех операций:

FIND(K) — поиск узла, в котором хранится пара (key, value) с key = K.

INSERT(K,V) — добавление в дерево пары (key, value) = (K, V).

REMOVE(K) — удаление узла, в котором хранится пара (key, value) с key = K.

Этот абстрактный интерфейс является общим случаем, например, таких интерфейсов, взятых из прикладных задач:

«Телефонная книжка» — хранилище записей (имя человека, его телефон) с операциями поиска и удаления записей по имени человека, и операцией добавления новой записи.

Domain Name Server — хранилище пар (доменное имя, IP адрес) с операциями модификации и поиска.

Namespace — хранилище имен переменных с их значениями, возникающее в трансляторах языков программирования.

По сути, двоичное дерево поиска — это структура данных, способная хранить таблицу пар

(key, value) и поддерживающая три операции: FIND, INSERT, REMOVE.

Кроме того, интерфейс двоичного дерева включает ещѐ три дополнительных операции обхода узлов дерева: INFIX_TRAVERSE, PREFIX_TRAVERSE и POSTFIX_TRAVERSE.

Первая из них позволяет обойти узлы дерева в порядке неубывания ключей.

Поиск элемента (FIND)

Дано: дерево Т и ключ K.

Задача: проверить, есть ли узел с ключом K в дереве Т, и если да, то вернуть ссылку на этот узел.

Алгоритм:

Если дерево пусто, сообщить, что узел не найден, и остановиться.

Иначе сравнить K со значением ключа корневого узла X.

o Если K=X, выдать ссылку на этот узел и остановиться.

o Если K>X, рекурсивно искать ключ K в правом поддереве Т. o Если K<X, рекурсивно искать ключ K в левом поддереве Т.

Добавление элемента (INSERT)

Дано: дерево Т и пара (K,V).

Задача: добавить пару (K, V) в дерево Т.

Алгоритм:

Если дерево пусто, заменить его на дерево с одним корневым узлом ((K,V), null, null) и остановиться.

Иначе сравнить K с ключом корневого узла X.

o Если K>=X, рекурсивно добавить (K,V) в правое поддерево Т. o Если K<X, рекурсивно добавить (K,V) в левое поддерево Т.

Удаление узла (REMOVE)

Дано: дерево Т с корнем n и ключом K.

Задача: удалить из дерева Т узел с ключом K (если такой есть).

Алгоритм:

Если дерево T пусто, остановиться

Иначе сравнить K с ключом X корневого узла n.

o Если K>X, рекурсивно удалить K из правого поддерева Т. o Если K<X, рекурсивно удалить K из левого поддерева Т.

oЕсли K=X, то необходимо рассмотреть три случая.

Если обоих детей нет, то удаляем текущий узел и обнуляем ссылку на него

уродительского узла.

Если одного из детей нет, то значения полей второго ребёнка m ставим вместо соответствующих значений корневого узла, затирая его старые значения, и освобождаем память, занимаемую узлом m.

Если оба ребёнка присутствуют, то

найдём узел m, являющийся самым левым узлом правого поддерева с корневым узлом Right(n);

присвоим ссылке Left(m) значение Left(n)

ссылку на узел n в узле Parent(n) заменить на Right(n);

освободим память, занимаемую узлом n (на него теперь никто не указывает).

Обход дерева (TRAVERSE)

Есть три операции обхода узлов дерева, отличающиеся порядком обхода узлов.

Первая операция — INFIX_TRAVERSE — позволяет обойти все узлы дерева в порядке возрастания ключей и применить к каждому узлу заданную пользователем функцию обратного вызова f. Эта функция обычно работает только c парой (K,V), хранящейся в узле. Операция INFIX_TRAVERSE реализуется рекурсивным образом: сначала она запускает себя для левого поддерева, потом запускает данную функцию для корня, потом запускает себя для правого поддерева.

INFIX_TRAVERSE ( f ) — обойти всё дерево, следуя порядку (левое поддерево, вершина, правое поддерево).

PREFIX_TRAVERSE ( f ) — обойти всё дерево, следуя порядку (вершина, левое поддерево, правое поддерево).

POSTFIX_TRAVERSE ( f ) — обойти всё дерево, следуя порядку (левое поддерево, правое поддерево, вершина).

INFIX_TRAVERSE:

Дано: дерево Т и функция f

Задача: применить f ко всем узлам дерева Т в порядке возрастания ключей

Алгоритм:

Если дерево пусто, остановиться.

Иначе

o Рекурсивно обойти левое поддерево Т. o Применить функцию f к корневому узлу.

oРекурсивно обойти правое поддерево Т.

Впростейшем случае, функция f может выводить значение пары (K,V). При использовании операции INFIX_TRAVERSE будут выведены все пары в порядке возрастания ключей. Если же использовать PREFIX_TRAVERSE, то пары будут выведены в порядке, соответствующем описанию дерева, приведѐнного в начале статьи.

Поиск в глубину (англ. Depth-first search, DFS) — один из методов обхода графа. Алгоритм поиска описывается следующим образом: для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них. Используется в качестве

подпрограммы в алгоритмах поиска одно- и двусвязных компонент, топологической сортировки.

Алгоритм поиска в глубину

Пусть задан граф G = (V,E), где V — множество вершин графа, E — множество ребер графа. Предположим, что в начальный момент времени все вершины графа окрашены в белый цвет. Выполним