Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алматинский университет энергетики и связи

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Кванттык механикагакириспе

.pdf

Скачиваний:

Добавлен:

01.05.2015

Размер:

1.3 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

d	2	Ψ		2m	0		2	x	2
			+			E −	m0 w			Ψ(x) = 0	(8.12)
		2		2			2
dx				H

Мынадай белгілеулер енгізелік:

2m0

m0 w

α =

β =

(8.13)

x 02

жєне ξ = x β =

- өлшемсіз айнымалы.

Сонда (8.12)-ші теңдеудің орнына мынадай теңдеу аламыз:

d 2 Ψ

+ (λ − ξ 2 )Ψ(ξ ) = 0

(8.14)

dξ 2

Бұл функцияның айнымалысы ξ → ±∞ ұмтылса(λ << ξ 2 ), онда (8.14)-ші теңдеу былай жазылады:

′′	2	Ψ∞ = 0	(8.15)
Ψ∞ − ξ

Бұл теңдеудің шешуін мынадай түрде іздестіреміз:

Ψ eaξ 2

(8.16)

∞

Бұл қатынасты (8.16)-ші теңдеуге қойсақ, онда

4a 2ξ 2 eaξ 2 − ξ 2 eaξ 2

= 0

(8.17)

Бұдан

4a 2 − 1 = 0

бұдан a = ± 1

Сонда (8.16)-шы шешудің орнына мынадай қатынас аламыз:

ξ 2

= С e 2

(8.18)

+ C

e 2

ξ → ±∞

∞

ұмтылғанда, толқындық

функция

шектелген болуы

керек шартынан,

C2 = 0, C1 = 1 болуы қажет. Енді (8.18) мынадай түрге келеді:

ξ 2

(8.19)

= e 2

∞

Сонда (8.14)-ші теңдеудің шешуі былай жазылады:

Ψ(ξ ) = Ψ U (ξ )e

U (ξ )

∞

Енді (8.14)-ші теңдеу мынадай түрге келеді:

U ′′(ξ ) − 2ξU ′(ξ ) + (λ −1)U (ξ ) = 0 (8.20)

Бұл теңдеудің шешуін қатар ретінде іздестіреміз:

U (ξ ) = a0 + a1ξ + a2ξ 2 + ...anξ n =	n	ξ k	(8.21)
	∑ ak
	k =1

(8.21)-ші қатарды (8.20)-шы теңдеуге қойып, қосындының индексін бір мєнге келтіреміз:

∑ ξ k [(k + 2)(k + 1)ak +2				− ak (2k + 1 − λ )] = 0			(8.22)
k =0
Бұл рекурренттік қатынас:		2k + 1 − λ
ak +2 =		2k + 1 − λ					(8.23)
						ak
		(k + 2)(k + 1)				ak
Бұдан k → ∞ жағдайда
	ak +2		≈		2
			≈
		ak			k

(8.21)-ші дəрежелі қатардың

eξ 2 түрінде өсетіндігін көреміз. Мұны

дєлелдеу үшін

функциясын қатарға жіктейік

ξ k +2

eξ 2 = 1 + ξ 2 + ξ 4

+ ξ 6

+ ... +

ξ k

+ ... = 1 + ξ 2 + ... + b

ξ k + ... + b

k +2

+1 !

бұдан

bk +2

+1 !

- жоғарыда айтылған тұжырым дєлелденді.
(8.21)-ші қатар kmax = n мєнімен шектеліп, an ¹ 0 жєне	an+2 = 0 болса, онда
λ = 2n + 1	(8.24)

(8.13)-ші қатынас бойынша λn = 2En / hw

Сонда кванттық механикадағы гармоникалық осциллятордың энергиясының меншікті мəндері:

				1
En = hw n +					(8.25)

				2
мұндағы п = 0, 1, 2, 3,...
Егер n=0 болса, гармоникалық осциллятордың нольдік энергиясы:
E0	=	1	hw		(8.26)

	2

(8.26)-ші рекуреттік қатынастан (8.21)-ші полиномның жұптылығы n санының мєнінің жұптылығына байланысты екендігін көреміз. Сондықтан полиномды былай жазуға болады:

(ζ ) = a

a0 , егер

n - жұп болса

ξ n + a

n−2

ξ n−2 + ... +

(8.27)

a1ξ , егер

n - тақ болса

an = 2n деп қабылдап,

(8.23)- ші рекуренттік формуладан калған коэффициенттердің

мєндерін анықтайық.

ак коэффициенттері үшін λ = 2n + 1 болғанда

немесе

ak (λ -1 - 2k ) = ak (2n +1 -1 - 2k ) = ak (2n - 2k ) = -ak +2 (k + 2)(k +1)

an−2 = -an (n -1)/(2 × 2) = -2n n(n -1)/1!

an−4 = -an−2 (n - 2)(n - 3)/(2 × 4) = 2n−4 n(n -1)(n - 2)(n - 3)/ 2!

an = 2n

жєне

λ = 2n + 1болатын (8.21)-ші

дєрежелі қатар Эрмит полиномы деп

аталады:

a1ξ , егер

n - тақ болса

n(n −1)

n(n −1)(n − 2)(n − 3)

U(ξ) = Hn (ξ) = (2ξ)n −

(2ξ)n−2 +

(2ξ)n−4 + ...+

(8.28)

a0 , егер

n - жұп болса

жеке жағдайларда H 0 (ξ ) = 1	егер	n = 0
H1 (ξ ) = 2ξ	егер	n = 1
H 2 (ξ ) = 4ξ 2 − 2	егер	n = 2
H 3 (ξ ) = 8ξ 3 -12ξ	егер	n = 3 …	(8.29)

Эрмит полиномын тұйықталған күйде де жазуға болады:

H n	(ξ ) = (-1)n e−ξ 2	d n e−ξ 2	(8.30)
		dξ n

Сонымен, энергияның меншікті Еп мєнін сипаттайтын толқындық функция мынадай түрде жазылады:

	(ξ ) = С	−	1	ξ 2		(ξ )	(8.31)
Y	(ξ ) = С	e 2		H	n	(ξ )	(8.31)
n	n				n

Сп -коэффициентін толқындық функцияны нормалау шартынан анықтауға болады.

+∞	Y		n	dξ = С2 x		+∞	−ξ	2	(ξ )dξ = 1
∫					0	∫ e		H 2
−∞		n		n		−∞		n

H n (ξ ) = (-1)n es 2

d 4 e−ξ 2

болғандықтан теңдіктің оң жағындағы интегралды былай

dξ n

+∞

−ξ 2

−2

түрлендіріп жазуға болады: ∫ e−ξ 2

H n2 (ξ )dξ = (-1) n ∫ H n

(ξ )

dξ =

−∞

dξ

Енді

(ξ )

d n H

= 2n × n!

dξ n

+∞

e−ξ

π ; екендігін ескерсек:

жєне ∫

dξ =

−∞

Cn =

(8.32)

2n × n!

π x0

Сонда толық шешу

Cn =

(8.33)

2n × n!

π x0

Сонымен, кванттық механикадағы гармоникалық осциллятордың энергиясының меншікті мєндері мен оларға сəйкес келетін меншікті функциялар (8.25)-ші жəне (8.33)-ші өрнектермен анықталады. Энергияның меншікті мəндерінің спектрлерін қарастырайық.

																	1		x	2
n = 0	E0 = 1 hw,			Y0 (x) =					1						−
n = 0	E0 = 1 hw,			Y0 (x) =					1				e 2 x0

		2

										πx0
									x
					2											1			x	2
					2											1			x	2
		3						x						−
														−
n = 1				Y1 (x) =						0
	E1 =		hw,							0		e 2						x0
																		x0

		2		2					πx0
								x
											- 2								1	x	2
																					2
				4
		5					x											−
																		−
n = 2				Y2 (x) =					0										2
	E2 =		hw,						0						e				2	x0
																				x0

		2				8 πx0
		2				8 πx0

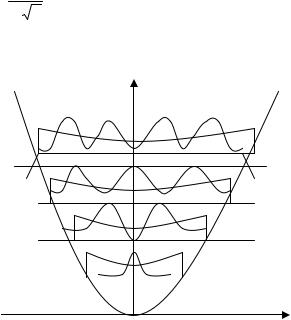
Бірінші толқындық функция x − тің ( x → ±∞ мєнінен басқа) қандай мєндерінде болса нольге тең болмайды. Екінші толқындық функция x = 0 нүктесінде нольге тең болады. Толқындық функция нольге тең болатын нүкте түйін деп аталады. Ал үшінші

толқындық функция x = ±x0 2 нүктелерінде нольге тең, яғни түйіндердің саны екіге тең

болады. Бұдан меншікті функциялардың түйіндерінің саны n кванттық санының мєндеріне тең болатындығын көреміз.

U (x)

n=0

│Ѱ2│2				ρ 2	2	E2	=			5		Hw
					2					5

							2
│Ѱ1│2	ρ 1	2				E1	=	3			Hw
		2						3

							2
│Ѱ0│2	ρ 0		2			E1	=		Hw
			2						Hw

							2

8.2-сурет. Энергияньң меншікті мəндері, кванттық сан п = 0, 1, 2 болғанда гармоникалық осциллятордың меншікті функцияларын классикалық теориямен (үзікті сызық) салыстыру

Графиктен п-нің үлкен мєндерінде кванттық механиканың нəтижелерінің классикалық физиканың мєндеріне жуық келетіндігін көреміз.

§ 3. Гармоникалық осциллятордын нольдік энергиясы жəне анықталмағандық қатынас

E = hw n +	1	қатынастан n = 0 тең болғанда гармоникалық осциллятордың
E = hw n +		қатынастан n = 0 тең болғанда гармоникалық осциллятордың
	2
	2				1
энергиясының нольге тең болмайтындығын көреміз.			E0	=	1	Hw - бұл шама
энергиясының нольге тең болмайтындығын көреміз.			E0	=		Hw - бұл шама
				2

гармоникалық осциллятордың нольдік энергиясы деп аталады.

Ал, жартылай кванттық Бор теориясы бойынша негізгі күйде гармоникалық осциллятордың энергиясы нольге тең болады. Шредингер теориясындағы гармоникалық осциллятордың нольдік энергиясының болуы анықталмағандық қатынастың яғни бөлшектердің толқындық қасиеті бар екендігінің тікелей салдары екендігін дєлелдейік. Гейзенбергтің анықталмағандық қатынасын мынадай түрде жазалық:

	×		³	h 2	(8.34)
x 2		p 2

4

Гармоникалық осциллятордың толық энергиясының орта мəні:

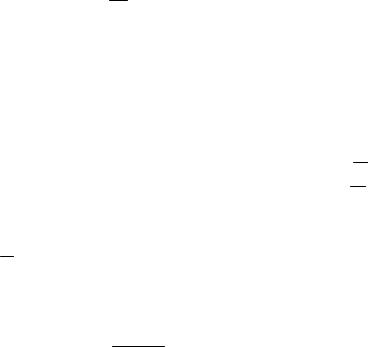
	=		=	p 2	+	m0 w2		(8.35)
							x2
E		H

				2m0	2

Егер мұндағы импульстің квадратының орнына (8.34)-ші қатынастағы импульстің мєнін қойсақ:

	³	h 2	+	m0 w2		(8.36)
					x 2
E
		8m0 x 2
			2

(8.36)-шы қатынастан гармоникалық осциллятордың энергиясының x2 - тың қаңдай мєнінде де нольге тең болмайтындығын көреміз. Шынында да, егер x 2 ® 0 ұмтылса,

(8.36)-шы өрнектегі бірінші мүше шексіздікке ұмтылады. Ал егерде x 2 ® ¥ болса, онда (8.36)-шы теңдеудің екінші мүшесі шексіздікке ұмтылады. Енді гармоникалық

осциллятор энергиясының x2 - тың қандай мєнінде минимум мəнге тең болатындығын

анықталық. Ол үшін (8.36)-шы қатынасты x2 бойынша дифференциалдап, нольге теңестіреміз:

m0 w2

(x2 )

= 0

(8.37)

8m0

бұдан

(8.38)

x 2

2m0 w 2

(8.38)-ші қатынасты (8.38)-ға қойьш, энергияның минимум мəнін анықтаймыз:

E ³

(8.39)

Сонымен гармоникалық осциллятордың

нольдік энергиясының

E0 =

екендігін көреміз. Гармоникалық осциллятордың нольдік энергиясының болуы микробөлшектің толқындық қасиетінің бар болуының тікелей салдары. Егер осциллятордың энергиясы нольге тең болса, бөлшек тыныштық күйде болуы керек. Шектің импульсі мен координаты бір уақытта нольге тең дəлдікпен белгілі болады, бұл Гейзенбергтің анықталмағандық қатынасына қайшы келеді. Көптеген тєжірибелік деректер кванттық теорияның тұжырымының дұрыс екендігін көрсетеді.

Кристалдың температурасы өзгергенде онда шашырайтын жарықтардың да өзгеретіндігін дєлелдейтін тєжірибені қарастырайық. Жарықтың шашырауы атомдардың тербелісіне байланысты. Температура төмендеген сайын, классикалық механика бойынша, атомдардың тербеліс амплитудасы да нольге дейін төмендейді жєне жарықтың жайылып шашырауы қажет. Ал, кванттық механика бойынша температура төмендегенде (T ® 0) тербелістің орташа амплитудасы нольге емес, осциллятордың нольдік энергиясының болуына байланысты, белгілі бір шекті мєнге ұмтылады. Сондықтан жарық кристалдан жайылып шашырауы тиіс. Кристалдан шашыраған жарықтардың қарқындылығын өлшеу нєтижесінде гармоникалық осциллятордың нольдік энергиясының болатындығы тєжірибеде дєлелденген.

n′ = n -1

§ 4. Гармоникалық осциллятордың сұрыптау ережелері

Гармоникалық осциллятордың сєуле бөліп шығару мəселесін кванттық теория тұрғысынан қарастырайық. Ол үшін мынадай штрицалық элементтерді

				*		ˆ
X n′,n =∫ Ψ n1					XΨn dx
есептеу қажет. Мұндағы
			1		x		2
	(x) = C								x
			2		x
Ψ			2		x	0
		e				0	H
		e					H
n	n							n
								x0

(8.40)

(8.41)

(8.41)-ші қатынасты (8.40)-шы матрицалық элементтерге қойсақ, онда

n−1

X n′,n

= x0

δ n′+1,n

δ n′−1,n

(8.42)

(8.42)-ші формуламен берілген матрицалық элементтер нольден өзгеше болуы үшін n − бас кванттық сан мынадай мєндерге ие болуы қажет: жєне n′ = n +1. Яғни, гармоникалық осциллятордың сұрыптау ережелері:

Ñn = ±1

Сонда (8.42)-ші матрицалық элементтер түрге келеді:

	X n−1,n	=	X				n
	X n−1,n	=	X		0	2
						2

	X n+1,n	=	X				n + 2
	X n+1,n	=	X		0	2
						2
Сəуле шығару жиілігі				En − En−1
	wn,n−1	=		En − En−1
	wn,n−1	=				H
n=4								w	E4/h
n=3							w		E3/h
n=2		w							E2/h
n=1	w								E1/h
n=0
	w								E0/h

(8.43)

(8.44)

(8.45)

(8.46)

8.3-сурет. Гармоникалық осциллятордың рұқсат етілген өтулері.

Гармоникалық осциллятордың сєулені ерікті түрде тек жоғары энергиялық деңгейден төменгі деңгейде орын ауыстырғанда ғана бөліп шығаратындықтан, сєуле шығару қарқындылығы мынадай қатынастан анықталады:

Wn,n−1 =	2e02 w2	Hx × n =	2e02 w2	(En E0 )	(8.47)
	3m0 c3		3m0 c3

9 ТАРАУ. КӨРІНІСТЕР ТЕОРИЯСЫНЫҢ НЕГІЗДЕРІ

Шредингер теңдеуі кеңістіктік координаталар мен уақытқа тєуелді толқындық функциямен сипатталады. Бұл жағдайда толқындық функция координаталық көріністе берілген деп айтылады.

Кванттық механикада координаталық көріністен басқа импульстік, матрицалық (энергетикалық) жəне тағы басқа да көріністер пайдаланылады.

Гармоникалық осциллятор теориясы негізінде бұл көріністерді жєне олардың арасындағы байланысты талқылайық. Осы мақсатта классикалық теориядан белгілі импульс пен координатаның арасындағы байланысты сақтай отырып, гамильтонианды былай жаза аламыз:

	ˆ 2		m0 w	2
ˆ	P x		m0 w		ˆ	2	(9.1)
H =	2m0	+	2		X		(9.1)
	2m0		2

пен арасындағы коммутативтік қатынас мынадай түрде болатындығы белгілі:

ˆ	ˆ ˆ ˆ		H	(9.2)
Px	X - XPx	=	i	(9.2)
			i

Осы шартты қанағаттандыру үшін кванттық механикада əрқайсысы өзінің көріністерімен байланысты болатын əртүрлі əдістер қарастырылады. Біз негізі үш көріністі жəне олардың арасындағы байланысты қарастырамыз.

1. Координаталық көрініс (х-көрініс)

Импульсті оператор ретінде қарастырып, х-ті сан деп алайық:

ˆ	=	H d	(9.3)
Px
		i dx

шамасы (9.2)-теңдікпен Y(x) - толқындық функциясына єсер еткен			жағдайда

ˆ операторының меншікті мєні болып табылады:

ˆ	ˆ ˆ ˆ	H
(Px	X - XPx )Y(x)=	i	(9.4)
		i

(9.3)-ші қатынасты (9.1)-ші қатынасқа қойсақ гамильтониан мынадай түрде жазылады:

ˆ	H 2	d 2		m0 w2		2	(9.5)
H =			+		X
	2m0	dx 2		2

Бір өлшемді гармоникалық осциллятор үшін Шредингер теңдеуінен ( x-көріністе)

	2		d 3
E - Ax		+ B			Y(x)= 0	(9.6)
E - Ax		+ B		2	Y(x)= 0	(9.6)
			dx	2
			dx

m0 w2

Мұнда,

A =

, B =

, x0 =

4 B

(9.7)

m0 w

2m0

энергияның меншікті мєндерін табамыз:

En = Hw n +

(9.8)

мұндағы: n = 0,1,2,3,...

Ал меншікті функциялар мынадай қатынаспен анықталады:

			1		x	2
Y (x) =		1

					x0
				e 2	x0		(9.9)
	2n	× n!		e 2			(9.9)
n	2n	× n!	π ¢x0
n

жəне олар нормалау шартын қанағаттандырады:

∞	Yn (x)	2	(9.10)
∫	Yn (x)	dx = 1	(9.10)
−∞
−∞

Кванттық теорияның негізгі қағидалары бойынша тєжірибеде бақыланатын шамалар операторлардың орташа мєндері больш табылады, ал толқындық функцияның өзі көмекші роль атқарады. Гармоникалық осциллятор теориясында маңызды шамалардың бірі координаталардың матрицалық элементтері:

xn′n

∞

* ˆ

9.11)

∫

Yn′ xYn dx

ал импульс үшін:

−∞

Pn′n

∞

* H d

Yn dx

(9.12)

∫

n′ i

−∞

Соңғы

интегралды шешу

үшін

гармоникалық

осциллятордың

толқындық

функциялары мен єртүрлі мəндерінің арасындағы қатынастарды аламыз:

n +1

x × Y = x

(9.13)

n−1

n+1

dYn

n +1

= -im

n−1

(9.14)

i dx

n+1

толқындық функциялардың ортонормалау шартын ескере отырып,

∞

∫ Yn*′Yn dx = δ n′n

−∞

координатаның матрицалық элементтері үшін 0-ден өзгеше болатын төмендегідей мєндерді табамыз:

xn−1,n	=	n	, xn+1,n = x0	n +1	(9.15)
				2
	2
жəне импульс үшін
Pn−1,n = -im0 wxn−1,n , Pn+1,n = -im0 wxn+1,n					(9.16)

§ 2. Импульстік көрініс (Р— көрініс)

ˆ	ˆ ˆ ˆ	H	қатынасында импульсті жєй сан деп қабылдап,					ал коорданатаны
Px	X - XPx =	i	қатынасында импульсті жєй сан деп қабылдап,					ал коорданатаны
		i
оператор деп алайық:
				ˆ	H d			(9.17)
				X -
				X -	i dP
					i dP
Бұл оператордың енді импульске тəуелді толқындық функцияға єсері
нєтижесінде мына теңдеу орындалуы керек:							ϕ (P)
			ˆ	ˆ ˆ	ˆ	H
			(Px	X - XPx )ϕ (P) =		i		(9.18)
						i

Гармоналық осциллятор теориясын импульстік көріністе тағайындайық:

	ˆ 2		m0 w	2
ˆ	P x		m0 w			2
H =	2m0	+	2		X
	2m0		2

теңдеуіне (9.17)-ден x − тің операторлық мəнін қойсақ мынадай қатынас аламыз:

	2		d
E - A1 P		+ B1		ϕ (P) = 0	(9.19)
E - A1 P		+ B1	dP 2	ϕ (P) = 0	(9.19)
			dP 2

мұнда	A1 =	1	,	B1	m0 w2 H	2	(9.20)

		2m0			2

Бұдан гармоналық осциллятор үшін х-көріністен р-көрініске ауысқан кезде толқындық теңдеуге басқа белгілеулер енгізілетіндігін көреміз:

λ =	E	=	2E
λ =		=
1	A1 × B1		Hw
	A1 × B1		Hw

Сонда негізгі теңдеу мынадай түрде жазылады:

ϕ ¢¢ + (λ -η 2 )ϕ = 0

(9.21)

Бұл теңдеуді шешу нєтижесінде p − көріністегі

энергияның меншікті

мєндері мен

меншікті функцияларын анықтаймыз:

λ1Hw

Hw n

(9.22)

(- i)

ϕ n (P) =

(9.23)

× H n

2n × n! πP

толқындық функция ϕ (P) ортонормалау шартын қанағаттандыруы керек:

∞

∫ dP ×ϕ n*′ (P)ϕ n (P) = δ n′n

(9.24)

−∞

Бұл жағдайда ϕ (P) - Y(x) толқындық функциясының Фурье-бейнесі болып табылады:

Y(x) =

∫ Y(P)e H

(9.25)

2πH

−i

ϕ (P) =

∫ Y(x)e H

(9.26)

2πH

Егер мынадай қатынасты ескерсек

∫ dPe−i

(x− x′)

= δ (x - x¢)

2πH

толқындық функция:

(x− x′)

Y(x) =

∫ dx¢Y(x¢)∫

−i

dPe H

2πH

Фурье түрлендіруді пайдаланып, жəне:

Yn (x) =

−

× H n

2n × n!

πx0

екендігін ескерсек, импульстік толқындық функция:

ϕ n (P) =

∞

∫ dxe

2πH

2n × n! πx0

−∞

∞

−

ξ 2

∫ dξe 2

2π

2n × n!

πx0

−∞

−i

−

× e

H n

× e

−i

Px0

(ξ )

H n

(9.27)

(9.28)

ϕ (p)- толқындық функцияны импульстер кеңістігінде анықтағаннан кейін

координаталар мен импульстер үшін матрицалық элементтерді төмендегідей өрнектер бойынша табамыз:

*			H d
xn′n = ∫ Y	-			ϕ n dP	(9.29)

n′			i dP
	*		ˆ		(9.30)
Pn′n = ∫ ϕ n′		×Pϕ n dP

§ 3. Матрицалық көрініс

(9.2)-ші қатынасты импульс P мен X − координатаны матрицалар түрінде жазу арқылы да қарастыруға болады:

ˆ	ˆ		ˆ ˆ			H
(Px	X )-		(XPx )=					I		(9.31)
мұндағы: I − бірлік матрица. Гамильтониан:						i
мұндағы: I − бірлік матрица. Гамильтониан:
	ˆ	2		m0 w	2
	ˆ				2
ˆ	(Px )							ˆ	2
H =	2m0		+	2			(X )			(9.32)
	2m0			2

Бұл жағдайда (9.17) жєне (9.18)-ші қатынастардағы матрицалық элементтер мынадай үзіліссіз диагональды матрицалар құрайды:

(x) =	х10
	х20
	х00

...

		...						0 ...
х01	х02	...		0	1/2	0		0 ...

х11	х12	...		1/2 0		2/2 0...				(9.33)
			= x =							(9.33)
х21	х22	...		0	2/2	0	3/2		...
...				... ... ... ... ...
...	... ...			... ... ... ... ...

<<< < Предыдущая 1 2 3 4 5 67 / 147 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.202543.35 Кб0Казахский язык.docx
#
01.05.20151.04 Mб142Казахский язык.pdf
#
01.05.2025450.81 Кб0Капарова Ф курсач есназаров.docx
#
01.05.201546.33 Кб14карамель.docx
#
01.05.2015687.36 Кб19Квантовая+физика.pdf
#
01.05.20151.3 Mб45Кванттык механикагакириспе.pdf
#
01.05.201571.76 Кб49Кедейшілік жне оны белгілері.docx
#
10.03.2016168.96 Кб3КИБ-Б416-5В100200-ru-150702-Зуева Е.А. Информатика.doc
#
01.05.20251.42 Mб0Ким Л.Н. М2, Ряды.doc
#
01.05.2015214.02 Кб33Коллоквиум Квантовая.doc
#
01.05.2015145.92 Кб52Коллоквиум Колебания.doc