Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алматинский университет энергетики и связи

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Кванттык механикагакириспе

.pdf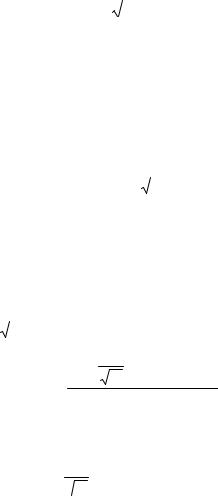

Скачиваний:

Добавлен:

01.05.2015

Размер:

1.3 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1410 11 12 13 14 > Следующая >>>

					1	ρ				(12.10)
	R∞ = e 2

2) r → 0 болғанда				L(L + 1)
R¢¢ +	2	R¢	-				R		= 0	(12.11)
	ρ
		∞				ρ 2		0

(12.11)-ші теңдеудің шешуін

= ρ q

деп қарастырамыз. Енді

q(q +1) - L(L +1) = 0

бұдан q 2 + q - L(L +1) = 0

= L × q2 = -(L +1)

q1,2 = -

± L +

;

Сонда:

= C ρ L + C

ρ −(L+1)

C1 = 1, C2

= 0 болғандықтан

= ρ L

(12.7)-ші теңдеуді былай түрлендіріп жазайық:

d 2 (R × ρ )

L(L +1)

(ρR) = 0

dρ

(12.16) теңдеудің жалпы шешуін мынадай түрде қарастырамыз:

R = R0 × R∞ ×U (ρ )

ρU (ρ )

Ал, (ρR) = ρ L+1e

Сонда (12.17)-ші негізгі теңдеуіміз мынадай түрге келеді:

ρU ¢¢ + [2(L +1) - ρ ]U

¢ +

- L -1 U (ρ ) = .0

(12.12)

(12.13)

(12.14)

(12.15)

(12.16)

(12.17)

(12.18)

(12.19)

(12.19)-шы теңдеудің шешуін дєрежелі қатар түрінде іздейміз
U (ρ ) = ∑ av ρ v	(12.20)
v=0

Бұл шешуді (12.19)-ші теңдеуге қойып, индекстерін бір мєнге келтірсек мынадай өрнек аламыз:

	v		B
∑ ρ		av			- L -1	+ av+1	[v(v +1)+ 2(v +1)(L +1)]	= 0	(12.21)

				A
v=0				A

B - L -1 - v
A	(12.22)
av+1 = - [v(v +1) + 2(v +1)(L +1)]av	(12.22)

(12.20)-шы қатарды максимум к мєнімен шектеп, aк ¹ 0, aк+2 = 0 деп алсақ, (12.22)-ші қатынастан

B	+ v = n	(12.23)
L +1

Мұнда п-1,2,3,... бас кванттық сан, L = 0,1,2,...; к = 0,1,2,... Осы өрнектерді ескергенде (12.20)-шы қатар мынадай түрде жазылады:

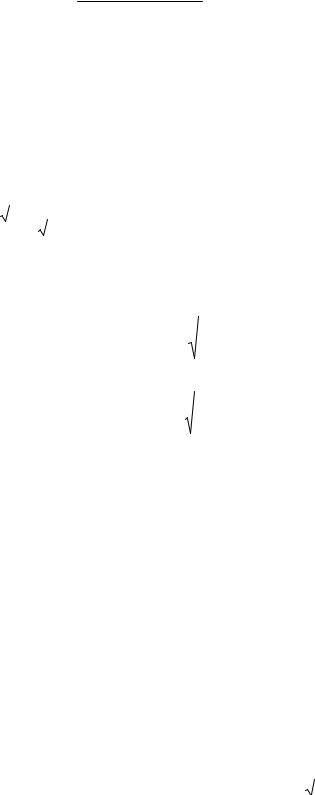
U = (− 1)к ρ к −					к(к + s)	ρ к−1 +	к+ j (к − 1)(к + s)к(к + s − 1)		ρ
					1!
=	∑	(− 1)		ρ к− j				2!
			к+ j		к!(к + s)!
	к				j!(к − j)!(к + s − j)!
	j =0

к−2 ... =

(12.24)

(12.24)-ші қатар к − ретті жалпыланған Ляггер			полиномы деп аталады. Мұндағы
S = 2L + 1. Ляггер полиномын тұйықталған түрде де жазуға болады:
U =Q s (ρ ) = e ρ ρ −s	d к		(e− ρ × ρ к+s )	(12.25)
	dρ
к		к

Сонда толқындық функцияның радиалдық теңдеуінің шешуі

1		ρ ρ L Q 2nL+−11 (ρ )
Rnl (ρ ) = Cnl e
	2

мұндағы ρ = 2

= n,

сонда

ρ =

Ar ,

na0

H 2

− бірінші

Бор

орбитасының

радиусы. Cnl − коэффициенті

m0 e2

функцияның нормалау шартымен анықталады:

3 / 2

n(n − L − 1)(n + L)!

na0

(12.26)

радиалдық

(12.27)

Енді

3 / 2

2Zr L

R (r ) =

na0

n(n − L − 1)(n + L)! na0

(12.28)

2L+1

× e

2Zr

na0

n−L−1

na0

Толық толқындық функция

(r,θ ,ϕ ) = R

(r )Y m (θ ,ϕ )

(12.29)

n,L

Энергияның меншікті мəндері:

= −

Z 2 e04

= −R

HZ 2

(12.3)

2a0 n2

n 2

− R =

e04 m0

− Ридберг тұрақтысы.

2H3

n = 1, m = 0. Бұл

Сутегі

тєріздес атомның негізгі

күйлерін

карастырайық:

жағдайда толқындық функция:

= R

(r )Y 0 (θ ,ϕ )

(12.31)

1,0,0,

1,00

мұнда

Y 00 (θ ,ϕ ) =ρ 00 (θ )Φ 0

(ϕ ) =

(12.32)

4π

Ψ1,0,0, = Ce

сонда

(12.33)

(12.33)-ші толқындық функцияның нормалау шарты мынадай түрде жазылады:

∫ Ψ*1,0,0 Ψ1,0,0 d 3 x =∫ Ψ*1,0,0 Ψ1,0,0 r 2 drdΩ

Бұл қатынасқа Y1,0,0 - функциясының мєндерін қойып жєне бұл функцияның

θ,ϕ −бүрыштарына тєуелсіздіктерін ескерсек:

∞2Z

C 2 × 4π ∫e na0 r 2 dr = 1

бұдан	С =	1	Z	3 / 2



		4π a0

Сонда ең төменгі кванттық күйдің толқындық функциясы:

	1	Z	3 / 2		Zr
Y =	1	Z			a		(12.34)
				e		0
				e		0
1,0,0,
1,0,0,	π a0
	π a0
Ал сутегі тєріздес атомның энергиясының меншікті мєндері							(12.35)
E = -RHZ 2							(12.35)
1

Энергиялық деңгейлер қосымша деңгейлерге негізгі күйде бөліктенбейді. Себебі азғын

күйлердің саны:

S = n2

қатынасымен анықталынады:

n =1, S =1, ал екінші n = 2 деңгей

төрт деңгейшелерге бөліктенеді:

n = 2

Y ; Y

; Y ; Y ; E

= -

RHZ 2

S = 4

2,1,0

2,1,−1

2,1,1

2,0,0

n = 3

Y3,2,0 ; Y3,2,1 ; Y3,2,−1 ; Y3,2,2 ;

S = 9

; Y ; Y ; Y

; Y

= -

RHZ 2

3,2,−2

3,1,0

3,1,1

3,1,−1

3,0,0

§ 2. Сутегі тəріздес атомның кванттық теориясының нəтижелерін классикалық тұрғыдан сипаттау

Классикалық теорияда

P 2r

= E +

Ze02

Pϕ2

(12.36)

2m0 r 2

2m0

шамасының нольден үлкен болатындығы белгілі. Эллиптикалық

орбиталар үшін

(E = -

< 0)

бұл шарт орындалады,

егер

радиус

мынадай аралықта

жатса:

rmin << r £ rmax .

Ал радиустың бұл мəндері

(13.36)-шы

қатынасты

нольге

теңестіру

арқылы табылады. Энергияның (13.30)-шы кванттық мəнін пайдалансақ:

rmax

1 ± 1 -

Pϕ

(12.37)

n2 H

min

Егер полярлық координаттарда жазылған эллипс теңдеуін пайдалансақ:

		r =	P		(12.38)
		r =	1 + ε cosϕ		(12.38)
мұндағы параметр p =	b 2	, яғни кіші жартылай осьтің − b квадратының a −үлкен
мұндағы параметр p =	a	, яғни кіші жартылай осьтің − b квадратының a −үлкен
	a

жартылай оське қатынасына тең, ал эллипстің эксцентриситеті ε =				a 2 - b2	, (12.38)-ші
				a	, (12.38)-ші
				a

қатынастан rmax жəне rmin шамалары үшін төмендегідей өрнектер аламыз:

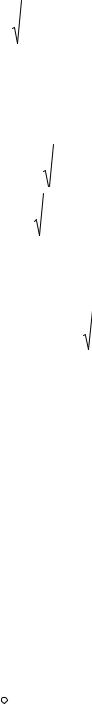
rmax

= a(1 + ε )

(12.39)

rmin

= a(1 - ε )

(12.40)

Бұл алынған мəндерді (12.37)-ші нəтижемен салыстырсақ

n 2 a0

= a

(12.41)

1 -

Pϕ2

= ε

(12.42)

n 2 H 2

Бұдан кванттық

n 2 a0

= a

шамасының

классикалық баламасы

эллипстің үлкен

жартылай

осіне,

ал эксцентриситеттің

(12.42)-ші өрнекке, Бор теориясындағы

Pϕ2 = n 2 × H 2

= H 2 × (L +1)2 жəне кванттық теориядағы

Pϕ2 = H2 L(L +1)

мəндерін қойсақ:

EБор

1 -

(L +1)2

(12.43)

Eкв =

1 -

L(L +1)2

(12.44)

L = (n -1) мəнінде

бұл қатынастардан Бор теориясы бойынша эксцентриситет нольге

тең болатындығын көреміз.

Ал кванттық теорияда L = n − 1

болғанда эксцентриситет

өзінің минимум мəніне тең болады:

E квmin =

(12.45)

Сондықтан, кванттық механикада кванттық күйлерді L = (n -1) болғанда классикалық дөңгелек орбиталардың баламасы ретінде ғана қарастыруға болады.

§ 3. Сұрыптау ережелері. Сутегі тəріздес атомның сəуле шығару спектрлері

Сутегі тəріздес атомның қандай жағдайда сəуле шығаратындығын анықтау, яғни сұрьштау ережелерін тағайындау үшін мынадай матрицалық элементтерді есептеу қажет:

(r )	n′L′m′		∫	*	R	3
					ˆ			(12.46)
	n m	=		Yn′L′m′ rYn,L,m d			x
	L
мұнда	Ψn,L,m		=Y mL (θ ,ϕ )RnL (r )
								(12.47)

Егер толқындық функцияны (12.46)-шы матрицалық элементтерге қойсақ

n′L′m

∞

m′

(r )

nLm

∫

dW(Y L

′

)

∫

L r

n′ ′

L 0

θ жəне ϕ бұрыштары бойынша интегралдау орбиталық кванттық сан

кванттық сан m бойынша сұрыптау ережелерін береді:

ÑL = L′ - L = ±1

Ñm = m¢ - m = 0,±1

(12.48)

L мен магниттік

Сонда (12.46)-шы теңдеудің орнына мынадай матрицалық элемент аламыз:

(r )n′L′m = const	δ m′m	δ L L			∞
(r )n′L′m = const	δ m′m	δ L L		±1	∫	R	L*	r 3 R	L dr	(12.49)
nLm			′,	±1	∫		n′, ′±1	n
	δ m′,m±1				0

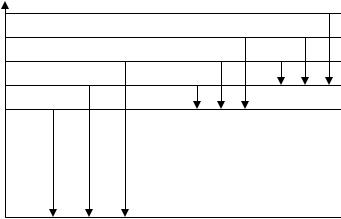
Егер (12.39)-шы қатынастағы интегралды есептейтін болсақ, онда бұл интегралдың кванттық сан n′ − тың қандай мəнінде де 0-ге тең болмайтынын көреміз, сондықтан сутегі тəріздес атомның сұрыптау ережелерін мынадай түрде жазуға болады:

ÑL = ±1, Ñm = 0,±1			(12.50)
n − кез келген мəнге ие бола алады.
Сəуле шығару жиілігі
wnn′ =	En - En′	= (n¢L¢)- (nL)	(12.51)

	H

мұндағы

= (nL) спектрлік терм деп аталады

En = -

Z 2 L02

= -RHZ 2

2a0 n 2

(nl )=

m0 L04

Z 2

RZ 2

ал R =

m0 L 04

2H3

n 2

wnn

= RZ

′

n¢

n 2

(12.52)

(12.53)

- Бальмер формуласы. Сутегі атомы үшін (z = 1, n = 1)- төменгі энергиялық күйге өтуге сəйкес келетін Лайман сериясы

	1			1
wлайμ	= (1s)- (np)= R
wлайμ	= (1s)- (np)= R	1	2	n	2
		1		n

мұнда n = 2,3,4,...

Бальмер сериясы үшін (n = 2)

Е, эВ

13,5

Бальмер сериясы

Лайман сериясы

12.2 сурет.

Сутегі атомының спектрлік сызықтары

WБ′ = (2s)- (np)

WБ′′ = (2 p)- (ns)

WБ′′ = (2 p)- (nd )

		1			1
WБ	= R			-
		2	2		n	2

n = 3,4,5,...

§4. Ядро қозғалысын ескеру

Сутегі тəріздес атом теориясын жасаған кезде атомның ортасындағы ядроның қозғалысын ескеріп, есептеулерге пайдаланған дұрыс. Ол үшін негізгі өрнекке кіретін m0 − электрон массасының орнына электрон мен ядроның келтірілген массасын алу

қажет:

яд

≈ m

−

(12.54)

келг

+ M яд

яд

Сонда Ридберг тұрақтысы мынадай түрде жазылады:

R =	m	келг		e4	= R		−	m	0
				0		1				(12.55)
			3
	2H					∞		M
									яд

Спектрлік термдердің (12.42)-ші өрнекпен берілетін мəндері де бұл жағдайда өзгешерек болады:

(nL) =	z 2 R		∞		−	m	0
				1				(12.56)
		2
	n					M
							яд

Ал сəуле шығару жиілігі мынадай өрнекпен анықталады:

2	−	m0	1		−	1
								(12.57)
				12			2
wnn′ = Z R∞ 1						n
		M яд n

Бұл			өрнектің		бұрышы	сəуле	шығару	жиілігінен	айырмашылығы
	−	m		көбейткішінде ғана.		Сəуле шығару жиілігі тек атом ядросының массасына
1	−	0		көбейткішінде ғана.		Сəуле шығару жиілігі тек атом ядросының массасына

		M яд

тəуелді болғандықтан, атомдардың массаларын спектроскопиялық əдіспен де анықтауға болады.

Осы əдіспен табиғатта ауыр сутегінің, иондалган гелий атомының бар екендігі дəлелденді. Күннің спектрін зерттеу нəтижесінде жиіліктері

			1			1
w	2n1	= R			−			(12.58)
				2			2
			2			n
							1

заңдылығымен орналасқан қосымша спектрлік сызықтары бар екендігі тағайындалды. Мұндағы n1 мынадай мəндерге ие болады:

n		=	5	, 3,	7	,	4,	9	, 5,...						(12.59)

1		2		2			2

Бұл серия сутегі атомының Бальмер сериясы (n = 3,4,5,...)													мен Пикеринг сериясы деп
аталатын, жартылай бүтін кванттық	сандарға						n1		=	5	,	7	,	9	,... ие болатын спектрлік

									2		2		2

сызықтардың қосындысына тең. Пикеринг сериясының сутегі атомдарының сəуле шығаруына байланысты ма, жоқ иондалған гелий атомының спектрлік сызықтары ма деген сұраққа жауап беру үшін тəжірибеден Ридберг түрақтысының мəнін анықтау қажет болды. Сутегі болған жағдайда Ридберг тұрақтысы

			1
RH	= R∞ 1	−		(12.60)

			1840

мəніне, ал, гелий атомы үшін

			1
RHe	= R∞ 1	−		(12.61)

			7360

болуы қажет.

Үқыпты жүргізілген спектроскопиялық тəжірибелер Ридберг түрақтысының (12.61)-ші өрнекпен сəйкес келетіндігін көрсетті. Яғни, Пикеринг сериясы иондалган гелий атомының спектрі болып табылады.

13 ТАРАУ. СƏУЛЕ ШЫҒАРУДЫҢ КАРАПАЙЫМ КВАНТТЫҚ ТЕОРИЯСЫ

§ 1. Ерікті жəне еріксіз кванттық өтулер. Эйнштейн коэффициентері

Классикалық электродинамика бойынша үдемелі қозғалыстағы зарядталған бөлшек жарық сəулесін шығару көзі болып табылады жəне уақыт бірлігі ішінде бөлініп шығатын сəуле энергиясы төмендегідей қатынастан анықталады:

			2e2
		Wkл =	2e2	R	(13.1)
			0	&&2
				r
R	R		3c3	r
R	R	− бөлшектің үдеуі.
мұнда r	= a	− бөлшектің үдеуі.
&&
Егер сəуле шығару көзі ретінде бір өлшемді гармоникалық осциллятор алынса,
		x = a × cos wt			(13.2)

онда сəуле шығару жиілігі осциллятордың механикалық тербеліс жиілігіне тең, ал


сəуле шығару энергиясы амплитуданың квадратына a 2 ,						пропорционал болады:
		Wkл =		e02 a 2 w4			(13.3)
		Wkл =			3c3		(13.3)
			2π		3c3
Егер	зарядтың	қозғалыс периоды T =	2π		, x = f (t )−	күрделі заңдылыққа бағынса,
Егер	зарядтың	қозғалыс периоды T =			, x = f (t )−	күрделі заңдылыққа бағынса,
			w
онда f (t )функциясын Фурье қатарына жіктеуге болады:
		x = ∑к ак cos wкt					(13.4)
яғни	сəулені жиілігі wк = кw(к = 1,2,3) осцилляторлар					жүйесі	бөліп шығарады деп
қарастыра аламыз.		Бұл жағдайда сəулені тек негізгі тон (к =1)					ғана емес, қалған кw

гармоникаларды бөліп шығарады, ал сəуле шығару қарқындалығы сəйкес гармониканың амплитудасының квадратына a к2 пропорционал болады.

Сонымен, классикалық теория бойынша жүйенің сəуле шығаруы осы жүйенің механикалық қасиеттерімен толық сипатталады. Атап айтқанда, сəуле шығару жиілігі жүйенің механикалық тербеліс жиілігіне не тең, не еселі, ал сəуле шығару интенсивтілігіне сəйкес гармониканың амплитудасының квадратына пропорционал болады.

Ал, кванттық механикада сəуле шығару мəселесін классикалық физикаға қарағанда мүлде өзгеше қарастырған жөн.

Себебі, кванттық механика бойынша бөлшек (бөлшектер жүйесі) электромагниттік сəулелерді жоғарғы энергиялық деңгейден төменгі энергиялық деңгейге ауысқанда ғана бөліп шығарады.

Сəуле шығару мəселесін кванттық механика тұрғысынан алғаш қарастырған Эйнштейн (1917 ж.) болды. Ол кванттық жүйенің ерікті жəне еріксіз түрдегі сəуле

шығаруларын А, В коэффициентерімен сипаттауды ұсынды жəне осы коэффициенттердің арасындағы байланысты тағайындады (13.1 сурет).

n		En
Ann΄	Bnn΄	Bn΄n

n΄		En΄

13.1 сурет. Ерікті жəне еріксіз өтулер

Сəуле шығарудың кванттық теориясының негізгі идеялары мынадай: атомның не атомдар жүйесінің бір электронының энергиясы En , n − кванттық күйде болсын. Сонда

бұл электронның уақыт бірлігі ішінде еркін түрде энергиясы En′ , n′ − күйге ауысуының

ықтималдығы Ann′ болсын. Бұл жағдайда электрон энергиясы	(13.5)
Hw = En - En′

фотон бөліп шығарады. Егер осы деңгейдегі қозған атомдардың саны N n болса, уақыт бірлігі ішінде жүйенің ерікті сəуле шығару қарқындылығы:

W еріктіс.ш.= N n × Hw × Ann′

(13.6)

Егер n − күйдегі атомдарды сыртқы электромагниттік сəулелердің əсері арқылы қозған күйге келтірсе, онда атомдар жоғарыдан-төмен еріксіз түрде сəуле шығарып ауыса бастайды. Екінші жағынан, сыртқы сəуленің əсерінен атомдар энергия жұтып, төменнен жоғары деңгейге де ауысулары мүмкін. Эйнштейн бөлшектердің еріксіз түрде, жоғарыдан төмен орын ауыстыру ыктималдылығын Bnn′ , еріксіз түрде

энергиясы төмен деңгейден жоғары деңгейге өтуін Bn′n коэффициенттері арқылы сипаттауды ұсынды. Еріксіз өтулердің саны спектрлік тығыздық ρw - ға пропорционал

деп есептесек, сəуле жұтып алу не бөліп шығару энергиясының мəндерін былай жазуға болады:

W	ерікс.cшіз.= N n × Вnn′ × Hwρw	(13.7)
W	ерікжутуcіз= N n′ × Вn′nn × Hwρw	(13.8)

мұнда N n′ - n′ деңгейдегі атомдардың саны. Атомдардың жоғарыдан төмен жəне төменнен жоғары ауысуларының саны тең жағдайда қарастырайық:

N n Ann′ + N n ρw Bnn′ = N n′ ρw Bn′n

(13.9)

Яғни, қызған атомдар мен олар бөліп шығаратын жəне өздеріне кері əсер ететін сəулелер термодинамикалық тепе-теңдік күйде болсын. Бұл жағдайда атомдар мен бөлініп шығатын сəулелер тұйықталған жүйе құрайды. Электрондардың энергия бойынша үлестірілуі Максвеллдің үлестірілу заңдылығымен сипатталатындығын ескерсек

N n = C × e

N n′ = C × e

En′

(13.9)-ші теңдеу былай жазылады:

(13.10)

e kT

+ ρ

nn′

= ρ

n′n

e kT

nn′

Бұл теңдеудің екі жағында e En kT - ға көбейтіп, Hw = En - En′ екендігін пайдалансақ, спектрлік тығыздық үшін төмендегідей өрнек аламыз:

	Ann′
ρw =	Bnn′	(13.11)
ρw =	Bnn′ eHw kT -1	(13.11)

Bn′n

Абсолют қара дененің сəуле шығаруының спектрлік тығыздығы атомдар мен молекулалардың нақтылы құрылысына тəуелсіз болғандықтан (13.11)-ші формуланы Планк формуласымен:

ρw		=		Hw3		×	1		(13.12)
ρw		=	π 2 c3			×	eHw kT	-1	(13.12)
салыстыруға болады. Сонда:			π 2 c3				eHw kT	-1
салыстыруға болады. Сонда:
B		= B				= π 2 c3		A	(13.13)
	nn′				n′n		Hw3	nn′

Бұл қатынастардан еріксіз түрде жоғарыдан-төмен жөне төменнен-жоғары өтулердің ықтималдылығы Ann′ коэффициентіне пропорционал екендігін көреміз. Сондықтан,

атомдар мен молекулалардың сəуле шығаруын сипаттау үшін осы коэффициенттердің бірінің мəнін білсек жеткілікті.

2. Ерікті жэне еріксіз сəуле шығарулардың ыктималдылығын анықтау

Кванттық механика бойынша атомдағы электрондардың еріксіз түрде бір күйден екінші күйге орын ауыстыруы олардың сыртқы электромагниттік сəулемен əсерлесуінің салдары деп түсіндіріледі. Ал электрондардың ерікті, спонтанды түрде қозған күйден төменгі деңгейге ауысуын Шредингер теориясы тұрғысынан түсіндіру мүмкін болмады. Бұл мəселе кванттық электромагниттік өріс теориясына негізделген сəуле шығару теориясы жасалғаннан кейін ғана түсіндірідді. Бұл теория бойышиа электрондар тек нақты фотондармен ғана емес, виртуал – пайда болуы мүмкін, фотондармен де, яғни электромагниттік вакууммен де əсерлесе алады. Осындай əсерлесу нəтижесінде ғана жүйе спонтанды түрде сəуле шығарады. Электрондардың виртуал фотондардың өрісімен əсерлесуінің классикалық аналогы ретінде үдемелі қозғалыстағы зарядталған бөлшекке осы зарядтың өзі тудырған элек-тромагниттік өрістің кері əсер етуін сипаттайтын Планктың сəуле үйкеліс күшін қарастыруға болады:

R	=	2e2	R
		0	&&&
Fc.ш			r
Fc.ш		3c3	r
		3c3

Кейбір қосымша шарттар орындалғанда бұл электромагниттік өріс жарық сəулелері түрінде электроннан бөлінуі мүмкін, кванттық электродинамикада бұл құбылыс фотондардың виртуал күйден нақты фотондарға ауысуына сəйкес келеді.

Кванттық электродинамикаға сүйене отырып А жəне В коэффициенттерінің мəндерін дəл анықтауға, яғни кванттық сəуле шығару мəселесін толық шешуге болады. Классикалық сəуле шығару теориясын кванттық жағдайға жалпылап, А коэффициентінің мəнін анықталық. Бұл жалпылаудын нəтижесінде екінші ретті кванттауға негізделген кванттық теориямен сəйкес келетінін ескертеміз.

Классикалық физикада сəуле шығару энергиясын сипаттайтын (13.1)-ші өрнекті кванттық жағдайға аударайық. Ол үшін классикалық r шамасының орнына оның кванттық баламасын аламыз:

R	*	R	R R	3
r = ∫Y		(r , t )	ˆ		x	(13.14)
			rY(r , t )d

Екінші жағынан, кванттық теория бойынша уақыт бірлігі ішінде бөлініп шығатын сəуленің энергиясы

Wкв = g n g n′ Ann′ × Hw	(13.15)
мұндағы g n gn′ - n жəне n′ деңгейлерінде электронның	бар-жоқтығын сипаттайтын

коэффициенттер. Бұл коэффициенттердің ену себебі Паули қағидасы бойынша бір энергиялық деңгейде төрт кванттық сандары бірдей екі электронның болуы мүмкін еместігін ескеру қажеттілігінде. (13.1)-ші жəне (13.15)-ші өрнектерді салыстырып, (13.14)-ші формуланы ескерсек:

	2e 2
g n g n′HwAnn′ =			R	(13.16)
	0	&&
			r
	3c3

Соңғы теңдікте екі рет орта шама алынған,	алғашқысы	R	- кванттық орта шама,
		r
		&&
кейін сызықшамен белгіленген уақыт бойынша орташалау.
Атомдағы электрон энергиялы En жəне	En′ болатын тек екі күйде ғана бола

алсын. Сонда кванттық суперпозиция принципі бойынша толқындық функция:

R		i	Ent		i	Ent	(13.17)

Y(r , t )= Сn	еH			+ Сn¢еH

Бұл қатынасты ескергенде r − радиус вектордың кванттық механикалық орта

мəні:

+C *Cn¢e

2 r

n′

2 r

+C *Cn¢eiwt r

−iwt r

n′n′

nn′

n′n

мұнда

w = w

nn′

En - En′

ал матрицалық элементтер:

rn′n

= ∫ Yn′

(r )rYn

(r )d

төмендегідей шексіз матрица құрайды:

r00

r01

r02

(r )=

r10

r11 r12 K

K K K K

n 2

(13.18)

(13.19)

(13.20)

(13.21)

Бұл матрицаның жолдарын бағанаға, бағаналарын жолдарға ауыстырсақ, (13.20)-шы формуланың негізінде комплекс-түйіндес

r *	= r	(13.22)
nn′	n′n

матрица аламыз.

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1410 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.03.2025239.98 Кб0КАЗАКСТАН ТАРИХЫ.docx
#
01.05.20151.04 Mб142Казахский язык.pdf
#
01.05.201546.33 Кб14карамель.docx
#
01.07.2025111.1 Кб0кариотип значение.doc
#
01.05.2015687.36 Кб19Квантовая+физика.pdf
#
01.05.20151.3 Mб45Кванттык механикагакириспе.pdf
#
01.05.201571.76 Кб49Кедейшілік жне оны белгілері.docx
#
10.03.2016168.96 Кб3КИБ-Б416-5В100200-ru-150702-Зуева Е.А. Информатика.doc
#
01.05.20251.42 Mб0Ким Л.Н. М2, Ряды.doc
#
01.05.2015214.02 Кб33Коллоквиум Квантовая.doc
#
01.05.2015145.92 Кб52Коллоквиум Колебания.doc