
- •Некоммерческое акционерное общество алматинский институт энергетики и связи
- •Теоретические основы электротехники 3
- •Содержание
- •1 Лекция 1. Возникновение переходных процессов, законы коммутации, классический метод расчета переходных процессов
- •1.2 Классический метод расчета переходных процессов
- •2 Лекция 2. Расчет переходных процессов в цепях с одним накопителем энергии
- •3 Лекция 3. Переходные процессы в цепях с двумя накопителями энергии
- •4 Лекция 4. Расчет переходных процессов в разветвленных цепях, интеграл Дюамеля
- •5 Лекция 5. Операторный метод расчета переходных процессов, теорема разложения
- •6 Лекция 6. Схемы замещения элементов, основные законы электрической цепи, расчет переходных процессов операторным методом
- •7 Лекция 7. Основы спектрального анализа электрических цепей
- •8 Лекция 8. Токи и напряжения в длинных линиях, уравнения однородной длинной линии (общий случай), установившийся синусоидальный режим в однородной линии
- •9 Лекция 9. Бегущие волны, уравнения длинной линии в гиперболических функциях
- •10 Лекция 10. Однородная линия при различных режимах работы, линия без потерь
- •11 Лекция 11. Линия без потерь при различных режимах работы
- •12 Лекция 12. Основные понятия о нелинейных цепях, методы анализа нелинейных электрических цепей постоянного тока
- •13 Лекция 13. Графические и аналитические методы анализа нелинейных электрических цепей постоянного тока
- •13.3 Расчет нелинейных цепей методом эквивалентного генератора
- •14 Лекция 14. Основные понятия и законы магнитных цепей
- •15 Лекция 15. Общая характеристика задач и методов расчета магнитных цепей
- •16 Лекция 16. Нелинейные цепи переменного тока
- •17 Лекция 17. Основные величины, характеризующие электростатическое поле
- •18 Лекция 18. Основные теоремы и уравнения электростатического поля
- •19 Лекция 19. Расчёт электростатических полей
- •20 Лекция 20. Электрическое поле постоянного тока
- •21 Лекция 21. Магнитное поле постоянного тока
- •Список литературы
5 Лекция 5. Операторный метод расчета переходных процессов, теорема разложения
Цель лекции: познакомить с основами операторного метода, переходом от операторных изображений к временным функциям.
5.1 Основы операторного метода, отыскание операторных изображений некоторых функций.
Идея
– замена интегро-дифференциальных
уравнений алгебраическими путем замены
функций времени функциями некоторого
комплексного переменного
![]() ,
называемого оператором.
,
называемого оператором.
Заданная
функция времени
![]() –
оригинал. Функция
–
оригинал. Функция
![]() ,
полученная в результате замены переменной
– изображение. Эти функции не равны
друг другу. Поэтому между ними ставится
знак не равенства, а соответствия, т.е
,
полученная в результате замены переменной
– изображение. Эти функции не равны
друг другу. Поэтому между ними ставится
знак не равенства, а соответствия, т.е
![]() .
.
Преимущество операторного метода – решение системы алгебраических уравнений много легче решения системы дифференциальных уравнений.
Расчет операторным методом сводится к решению двух задач:
- перевод заданных временных функций в операторные (т.е. алгебраизация уравнений);
- перевод вычисленных в результате расчета операторных функций во временные.
Первая задача решается с помощью преобразования Лапласа
 .
(5.1)
.
(5.1)
Изображение
постоянной.
![]() .
.
 ,
т.е. величина, не зависящая от времени,
не зависит и от новой переменной.
,
т.е. величина, не зависящая от времени,
не зависит и от новой переменной.
Изображение суммы двух функций.
Пусть известны изображения
 ;
;
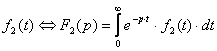 .
.
Найти
изображение
![]() .
.
Согласно (5.1):
 .
.
Изображение показательной функции.
Если
задано
![]() ,
где
,
где
![]() -
постоянная величина, то
-
постоянная величина, то
 .
.
![]() .
.
Изображение синуса и косинуса.
По
изображению показательной функции
находятся изображения
![]()
и
![]() .
По формулам Эйлера
.
По формулам Эйлера
![]() ,
,
![]() .
.
Можно
показать, что
![]() ,
,
![]() .
.
![]() .
.
Изображение производной.
![]() .
При нулевых начальных условиях
.
При нулевых начальных условиях
![]() ,
,
![]() .
.
Изображение интеграла.
Найдем
изображение
 ,
если известно изображение функции
,
если известно изображение функции
![]() .
.
 ,
,
где
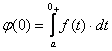 ,
,
![]() .
.
Если
![]() -
ток, протекающий через конденсатор, то
-
ток, протекающий через конденсатор, то
![]() -
заряд на его пластинах
-
заряд на его пластинах
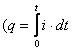 ).
Если в начальный момент конденсатор не
заряжен,
).
Если в начальный момент конденсатор не
заряжен,
![]() ,
то
,
то
![]()
 .
Таким образом, интегрированию функции
времени соответствует в операторной
форме деление изображение этой функции
на оператор
.
Таким образом, интегрированию функции
времени соответствует в операторной
форме деление изображение этой функции
на оператор
![]() .
.
Пример
- Найти
ток
![]()
![]() при
включении цепи
при
включении цепи
![]() на
постоянное напряжение
на
постоянное напряжение
![]() (см.
рисунок 1.1).
(см.
рисунок 1.1).
Уравнение электрического равновесия цепи имеет вид
![]()
![]() .
.
Переходим к операторным изображениям
![]() ,
,
![]() ,
т.к.
,
т.к.
![]() .
.
![]() .
.
В
операторной форме получим:
![]() и
изображение тока
и
изображение тока
![]() .
.
Для обратного перехода к временным функциям преобразуем выражение
![]()
 .
.
Известно,
что
![]() ,
а т.к. полученное изображение
,
а т.к. полученное изображение
![]() сходно
с указанным, то
сходно
с указанным, то
![]() .
.
5.2 Теорема разложения
Если
операторное изображение
![]() может
быть представлено в виде
может
быть представлено в виде
![]() ,
где
,
где
![]() и
и
![]() -
многочлены различных степеней
-
многочлены различных степеней
![]() ,
то оригинал определяется с помощью
теоремы разложения.
,
то оригинал определяется с помощью
теоремы разложения.
Пусть
![]() .
.
Теорема разложения применима к определению оригинала такой операторной функции при следующих условиях:
-
степень числителя
![]() степени
знаменателя, т.е.
степени
знаменателя, т.е.
![]() ;
;
-
все корни знаменателя
![]() ,
,
![]() ,
…
,
…
![]() ,
находимые из условия
,
находимые из условия
![]() ,
,
различны;
- ни один из корней знаменателя не совпадает с корнями числителя.
Согласно математическому анализу, дробь, удовлетворяющая этим условиям, может быть разложена в ряд, состоящий из простых дробей
![]() ,
(5.2)
,
(5.2)
где
![]() ,
,
![]() ,
…
,
…
![]() -
корни знаменателя.
-
корни знаменателя.
Найдем
коэффициенты уравнения (5.2). Для определения
коэффициента
![]() умножим
обе части равенства (5.2) на
умножим
обе части равенства (5.2) на
![]() ,
а затем приравняем
,
а затем приравняем
![]()
![]()
![]() .
(5.3)
.
(5.3)
Если
в (5.3) подставить
![]() ,
то в правой части остается только
,
то в правой части остается только
![]() ,
а в левой получается неопределенность,
т.к.
,
а в левой получается неопределенность,
т.к.
![]() и
и
![]() .Раскроем
ее
.Раскроем
ее
 ,
т.е.
,
т.е.
![]() .
.
Подставив
найденные значения коэффициентов в
![]() ,
получим
,
получим
![]()
 ,
но
,
но
![]() .
Следовательно
.
Следовательно
![]() -
теорема
разложения.
(5.4)
-
теорема
разложения.
(5.4)
Если
операторное изображение получилось в
виде
![]() ,
то теорема разложения запишется в виде
,
то теорема разложения запишется в виде
![]() ,
(5.5)
,
(5.5)
где
![]() и
и
![]() -
числитель и знаменатель дроби
-
числитель и знаменатель дроби
![]() при
при
![]() .
.
