
- •Некоммерческое акционерное общество алматинский институт энергетики и связи
- •Теоретические основы электротехники 3
- •Содержание
- •1 Лекция 1. Возникновение переходных процессов, законы коммутации, классический метод расчета переходных процессов
- •1.2 Классический метод расчета переходных процессов
- •2 Лекция 2. Расчет переходных процессов в цепях с одним накопителем энергии
- •3 Лекция 3. Переходные процессы в цепях с двумя накопителями энергии
- •4 Лекция 4. Расчет переходных процессов в разветвленных цепях, интеграл Дюамеля
- •5 Лекция 5. Операторный метод расчета переходных процессов, теорема разложения
- •6 Лекция 6. Схемы замещения элементов, основные законы электрической цепи, расчет переходных процессов операторным методом
- •7 Лекция 7. Основы спектрального анализа электрических цепей
- •8 Лекция 8. Токи и напряжения в длинных линиях, уравнения однородной длинной линии (общий случай), установившийся синусоидальный режим в однородной линии
- •9 Лекция 9. Бегущие волны, уравнения длинной линии в гиперболических функциях
- •10 Лекция 10. Однородная линия при различных режимах работы, линия без потерь
- •11 Лекция 11. Линия без потерь при различных режимах работы
- •12 Лекция 12. Основные понятия о нелинейных цепях, методы анализа нелинейных электрических цепей постоянного тока
- •13 Лекция 13. Графические и аналитические методы анализа нелинейных электрических цепей постоянного тока
- •13.3 Расчет нелинейных цепей методом эквивалентного генератора
- •14 Лекция 14. Основные понятия и законы магнитных цепей
- •15 Лекция 15. Общая характеристика задач и методов расчета магнитных цепей
- •16 Лекция 16. Нелинейные цепи переменного тока
- •17 Лекция 17. Основные величины, характеризующие электростатическое поле
- •18 Лекция 18. Основные теоремы и уравнения электростатического поля
- •19 Лекция 19. Расчёт электростатических полей
- •20 Лекция 20. Электрическое поле постоянного тока
- •21 Лекция 21. Магнитное поле постоянного тока
- •Список литературы
3 Лекция 3. Переходные процессы в цепях с двумя накопителями энергии
Цель лекции: познакомить с особенностями протекания переходных про-
цессов
в цепях с последовательным соединением
элементов![]() и при их подключении на постоянное
напряжение.
и при их подключении на постоянное
напряжение.
3.1
Переходный процесс в цепи
![]()

Так
как расчет с конденсатором удобнее
вести через
![]() ,
то
все
входя-щие в (3.1) величины выразим через
это напряжение
,
то
все
входя-щие в (3.1) величины выразим через
это напряжение
![]() ;
;
![]() ;
;
![]() .
Подставив эти выражения в (3.1),
.
Подставив эти выражения в (3.1),
получим линейное дифференциальное уравнение второго порядка
![]() .
.
Освободимся
от коэффициента при
![]()
![]() ,
(3.2)
,
(3.2)
где
![]() пр.
пр.![]() св.
св.
Определяем
![]() пр.
по
закону Ома. Принужденная составляющая
зависит от формы приложенного напряжения.
Если
пр.
по
закону Ома. Принужденная составляющая
зависит от формы приложенного напряжения.
Если
![]() ,
то
,
то
![]() пр.
пр.![]() .
Если
.
Если
![]() ,
то напряжение и ток установившегося
режима так же будут синусоидальными. В
этом случае расчет ведется в комплексной
форме, а затем находятся мгновенные
значения как функции времени.
,
то напряжение и ток установившегося
режима так же будут синусоидальными. В
этом случае расчет ведется в комплексной
форме, а затем находятся мгновенные
значения как функции времени.
Находим uС св., которая и определяет длительность и характер переходного процесса.
![]() .
(3.3)
.
(3.3)
Решением
(3.3) будет:
![]() .
(3.4)
.
(3.4)
Корни
характеристического уравнения
![]() определяются
как
определяются
как
![]() .
(3.5)
.
(3.5)
Значения корней зависят от соотношения параметров цепи. Может быть
три случая:
а)
![]() >
>![]()
![]()
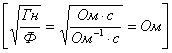 .
.
При
этом условии
![]() и
корни p1,
p2
получаются
вещественными, отрицательными, различными
по величине.
и
корни p1,
p2
получаются
вещественными, отрицательными, различными
по величине.
В
самом деле, если обозначить
![]() ,
где
,
где
![]() –
вещественное число, меньше чем
–
вещественное число, меньше чем
![]() ,
то
,
то
![]() <
0;
<
0;
![]() <
0. (3.5а)
<
0. (3.5а)
По
абсолютной величине |
![]() 1
| < |
1
| < |
![]() 2
|. Такой режим называется апериодическим,
т.к. ток и напряжение приближаются к
установившемуся режиму, не меняя своего
направления; б)
2
|. Такой режим называется апериодическим,
т.к. ток и напряжение приближаются к
установившемуся режиму, не меняя своего
направления; б)
![]() .
При этом условии
.
При этом условии
![]() и
корни
и
корни
![]() также
вещественные, отрицательные.
также
вещественные, отрицательные.
В
этом случае
![]() .
(3.6)
.
(3.6)
Этот режим называют критическим;
в)
![]() <
<
![]() .
В этом случае корни
.
В этом случае корни
![]() и
и
![]() комплексно-сопряженные
с отрицательной вещественной частью
комплексно-сопряженные
с отрицательной вещественной частью
![]() ;
;
![]() ,
(3.7)
,
(3.7)
где
![]() –
коэффициент затухания;
–
коэффициент затухания;
![]() =
=
![]()
![]()
![]() -
угловая частота собственных колебаний.
-
угловая частота собственных колебаний.
Такой режим называется периодическим или колебательным. Здесь происходит многократный обмен энергии между катушкой и конденсатором: энергия как бы переливается то в магнитное поле (когда растет ток), то в электрическое поле (когда растет напряжение на конденсаторе).
Постоянные интегрирования находятся из начальных условий.
![]() .
(3.8)
.
(3.8)
![]() .
(3.9)
.
(3.9)
При
![]() :
:
![]() ,
,
![]() .
(3.10)
.
(3.10)
Из
уравнений (3.10) легко определяются
![]() и
и
![]() .
.
3.2
Включение цепи
![]() на
постоянное напряжение
на
постоянное напряжение
Считаем, что цепь рисунка 3.1 включается на постоянное напряжение
![]() u
= U0
. Тогда
u
= U0
. Тогда
![]() и
начальные условия (3.10) примут вид
и
начальные условия (3.10) примут вид
![]() ;
;
![]() ,
откуда
,
откуда
![]() ,
,
![]() .
.
С учетом полученного из (3.8) и (3.9.) имеем
![]() ,
,
![]() .
(3.11)
.
(3.11)
Исследуем полученные выражения при разных значениях корней.
а) апериодический режим В этом случае, согласно (3.5а), имеем
![]() >
>
![]() ,
,
![]() >
>
![]() и
и
![]() >
>
![]() .
.
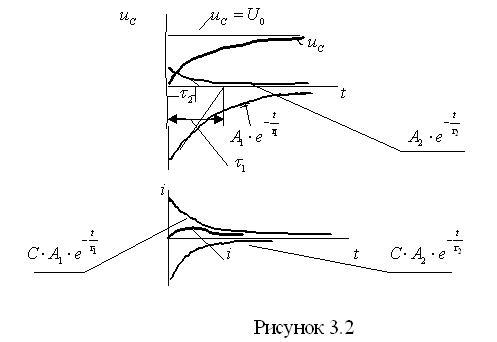
В
соответствии с этим графики
![]() и
и
![]() имеют
вид, представленный на рисунке 3.2.
имеют
вид, представленный на рисунке 3.2.
б)
колебательный
режим.
Так как в этом случае
![]() и
и
![]() –
сопряженные комплексы, то
–
сопряженные комплексы, то
![]() ,
а
,
а
![]()
![]() ,
,
где
![]() -
резонансная частота.
-
резонансная частота.
Подставим комплексные корни в выражения (3.11) и проведем некоторые
преобразования:
![]() =
=
![]() ,
,
т.к.
![]() .
(3.12)
.
(3.12)
Переведем стоящие в скобках комплексы в показательную форму (рисунок 3.3)
![]()
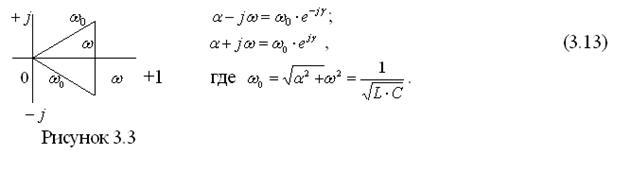
Подставив (3.13) в (3.12), получим
![]() .
(3.14)
.
(3.14)
Подобным же образом можно преобразовать выражение тока
![]() =
=![]() .
.
(3.15)
Если
учесть, что
![]() ,
то можно получить ток
,
то можно получить ток
![]() в
несколько ином виде:
в
несколько ином виде:
![]() .
.
Для
построения графиков
![]() и
и
![]() нужно
знать период собствен-
нужно
знать период собствен-
ных
колебаний
![]() и
постоянную времени
и
постоянную времени
![]() .
.
Порядок построения затухающей синусоиды.
1. По обе стороны от оси строятся огибающие.
2.
В том же масштабе, что и
![]() откладываются
доли периода (при этом надо учитывать
начальный угол).
откладываются
доли периода (при этом надо учитывать
начальный угол).
3. Вписывается синусоида, которая в точках максимума касается огибающих.
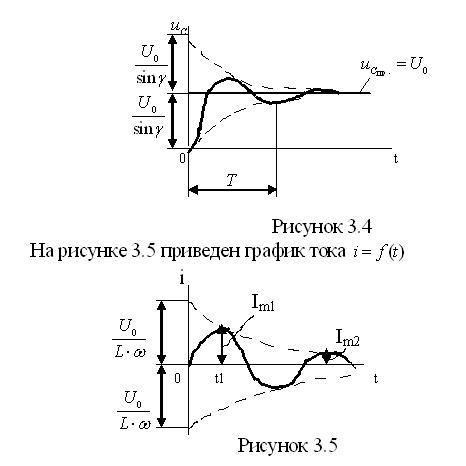
Так
как
![]() представляет
собой разность постоянной величины и
затухающей синусоиды, то для уменьшения
графической работы на рисунке 3.4 эта
синусоида построена с учетом знака,
причем линия
представляет
собой разность постоянной величины и
затухающей синусоиды, то для уменьшения
графической работы на рисунке 3.4 эта
синусоида построена с учетом знака,
причем линия
![]() использована
как ось, т.е. сразу построен график
использована
как ось, т.е. сразу построен график
![]() ,
а не составляющие этого напряжения.
,
а не составляющие этого напряжения.
Если
обозначить амплитуды напряжения и тока
через
![]() и
и
![]() ,
то их отношение
,
то их отношение
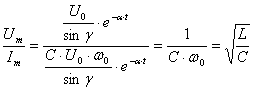 ,
т.е. равно волновому сопротив-лению.
Идеальный случай, когда
,
т.е. равно волновому сопротив-лению.
Идеальный случай, когда
![]() и
цепь можно считать сверхпроводя-щей.
При этом
и
цепь можно считать сверхпроводя-щей.
При этом
![]() и
и
![]() .
Но при
.
Но при
![]() энергия
будет переходить от магнитного поля к
электрическому без затухания. Отсюда
еще одно название
энергия
будет переходить от магнитного поля к
электрическому без затухания. Отсюда
еще одно название
![]() -
угловая частота незатухающих колебаний
и
-
угловая частота незатухающих колебаний
и
![]() -
период собственных незатухающих
колебаний. Угол
-
период собственных незатухающих
колебаний. Угол
![]() при
при
![]() получается
равным 900.
получается
равным 900.
В
реальных цепях
![]() и
процесс будет затухающим. Для оценки
быстро-
и
процесс будет затухающим. Для оценки
быстро-
ты
затухания сравним две соседние амплитуды
тока (или напряжения) с одинаковым
знаком. Пусть
![]() ,
,
![]() ,
т.к.
,
т.к.
![]() .
Отношение этих амплитуд
.
Отношение этих амплитуд
![]() (3.16)
(3.16)
называется
декрементом колебания. Он не зависит
от времени
![]() ,
а зависит лишь от параметров цепи
,
а зависит лишь от параметров цепи
![]() .
Обычно пользуются не им, а логарифмическим
декрементом колебания
.
Обычно пользуются не им, а логарифмическим
декрементом колебания
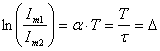 .
(3.17)
.
(3.17)
В
колебательных контурах стремятся
сделать
![]() как
можно меньше, т.к. тогда затухание в
контуре почти не сказывается. На графиках
как
можно меньше, т.к. тогда затухание в
контуре почти не сказывается. На графиках
![]() ,
т.е.
,
т.е.
![]() и
процесс затухает довольно быстро.
и
процесс затухает довольно быстро.
