2.2 Задание на лабораторную работу

2.2.1 Постройте структурные схемы систем (2.1) и (2.2) в среде VisSim.

2.2.2 Придавая различные значения k₁ и k₂ для системы (2.1), получите переходные характеристики (во времени) x₁(t) и фазовые портреты y=x₂=f(x₁).

2.2.3 Исследуйте зависимость t_пп=t(k₁,k₂, k₁/k₂).

2.2.4 Для системы (2.2) сформируйте закон переключения (2.10).

2.2.5 Исследуйте режимы с>λ, с=λ и с<λ; получите переходные процессы и фазовые портреты.

2.2.6 Для «скользящего» режима исследуйте процесс при изменении параметров а₁, а₂, в.

2.3 Требования к отчету

Отчет по работе должен содержать:

- структурные схемы;

- фазовые траектории при выбранных коэффициентах;

- переходные процессы;

- выводы по выполненным исследованиям.

3 Лабораторная работа №3. Исследования автоколебаний в нелинейной системе методом гармонического баланса

Цель работы: изучение метода гармонического баланса и приобретение навыков расчета параметров автоколебаний и моделирования нелинейных систем.

3.1 Общие сведения

Для приближенного определения автоколебаний в нелинейной системе можно применить метод гармонического баланса. Он основан на использовании частотных характеристик нелинейных систем, получаемых при гармонической линеаризации нелинейностей.

Основная идея заключается в том, что линеаризация нелинейностей систем производится на режиме автоколебаний, которые предполагаются близкими к синусоидальным. Это предложение оказывается близким для большинства автоматических систем, линейная часть которых является хорошим низкочастотным фильтром.

Если на вход статического нелинейного элемента с характеристикой y=f(x) подать гармонический сигнал x(t)=Asinωt, то на выходе устанавливаются периодические колебания, которые можно представить как сумму гармонических составляющих с помощью ряда Фурье.

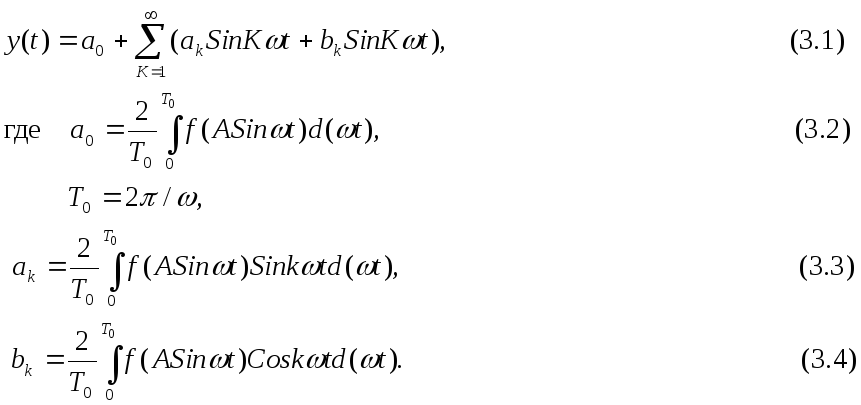
Предположим, что все гармоники, начиная со второй, имеют достаточно малую амплитуду по сравнению с первой, и ими можно пренебречь.

Тогда уравнение вынужденных колебаний напишется в виде:

или

где

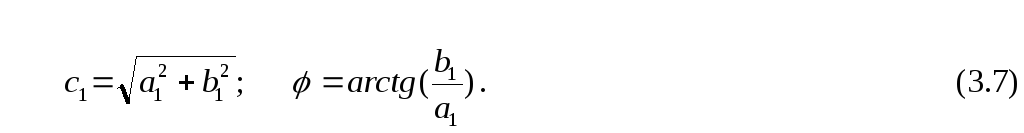Для симметричных нелинейностей а₀=0, то тогда

(3.8)

Сравнивая y(t) с x(t), можно ввести характеристики, аналогичные частотным характеристикам линейных систем (3.9) и инверсную АФХ (3.10)

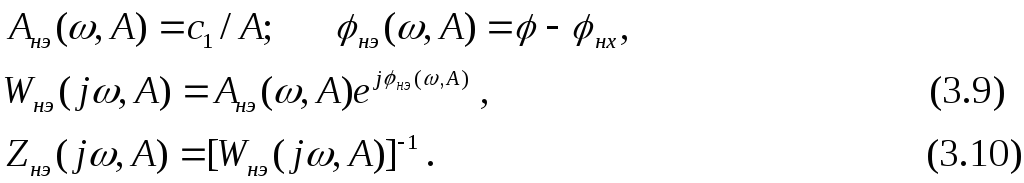
Нелинейная система в виде замкнутой системы может быть представлена в виде (см. рисунок 3.1).

Рисунок 3.1 – Нелинейная система

Если на вход нелинейного элемента подают гармонический сигнал с частотой ω₁, то, с учетом свойства фильтра линейной части, в замкнутой системе возникнут незатухающие колебания.

Это означает, что система находится на границе устойчивости, которой соответствует условие:

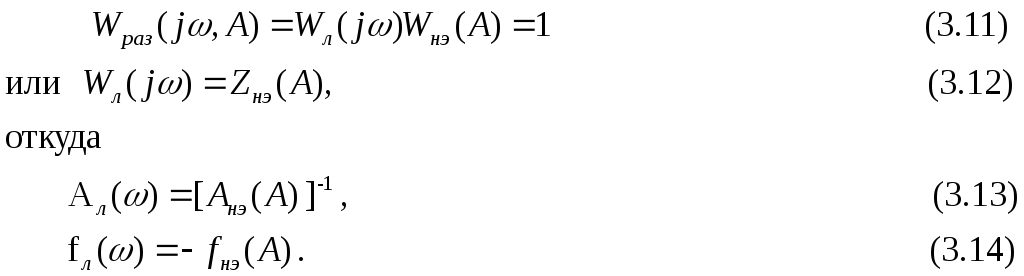
Если уравнения (2.13) и (2.14) имеют действительное положительное решение (ω_а, А_а), то в системе возможны автоколебания с частотой ω_а и амплитудой А_а.

Систему (2.13) и (2.14) можно решать графически. Для этого в плоскости комплексного переменного строят АФХ линейной части W_л(jω) и инверсную АФХ нелинейного элемента Z_нэ(А). Точка пересечения годографов W_л(jω) и Z_нэ(А) определяют амплитуду А_а и частоту ω_а. Если годографы не пересекаются, то автоколебания в системе невозможны. Метод гармонического баланса позволяет также ответить на вопрос, будут ли автоколебания устойчивы.

Пусть взаимное расположение кривых W_л(jω) и Z_нэ(А) таково, что увеличение амплитуды колебаний соответствует движению по кривой Z_нэ(А) вправо (см. рисунок 3.2). Тогда точки W_л(jω) и Z_нэ(А) соответствуют автоколебаниям. Если под воздействием возмущения амплитуда колебаний возрастает (А_а+ΔА_а), то новому состоянию нелинейного элемента будет соответствовать точка М₁, которая находится вне АФХ линейной части. При этом W_л(jω) < Z_нэ(А), значит, W_раз (jω, А)<1, и, следовательно, в этом состоянии система будет вести себя как устойчивая, т.е. амплитуда колебаний будет уменьшаться и через некоторое время станет равной исходной А_а.

Рисунок 3.2 –Устойчивое

автоколебание

Рисунок 3.3 -Неустойчивое автоколебание

Если под действием возмущения амплитуда автоколебаний станет меньше А_а, то новому состоянию системы будет соответствовать точка М₂, в которой система ведет себя как неустойчивая. Следовательно, амплитуда будет возрастать и вернется к исходному значению А_а.

Рисунок 3. 4 - Устойчивость состояния равновесия следящей системы

В качестве примера рассмотрим исследование устойчивости состояния равновесия следящей системы, структурная схема которой изображена на рисунке 3.4, если ее параметры В=1 В; k₁ k₂ =10 c^-1; T₁=10 c; T₂=1 c.

Для решения по структурной схеме запишем уравнение линейной части системы в виде

. (3.15)

Для нелинейного элемента имеем

u₁(t)=q(A)u(t) (3.16)

где

. (3.17)

Подставляя выражения (3.16) и (3.17) в уравнение (3.15), получим

. (3.18)

Применяя к уравнению (3.18) преобразование Лапласа при нулевых начальных условиях, запишем

. (3.19)

Из уравнений (3.19) найдем характеристическое уравнение

. (3.20)

Возможность существования периодического решения уравнения проанализируем с помощью критерия устойчивости Михайлова. Для этого в уравнение (3.20) подставим s=jω; тогда найдем

. (3.21)

Откуда, приравнивая действительную и мнимую часть нулю, получаем

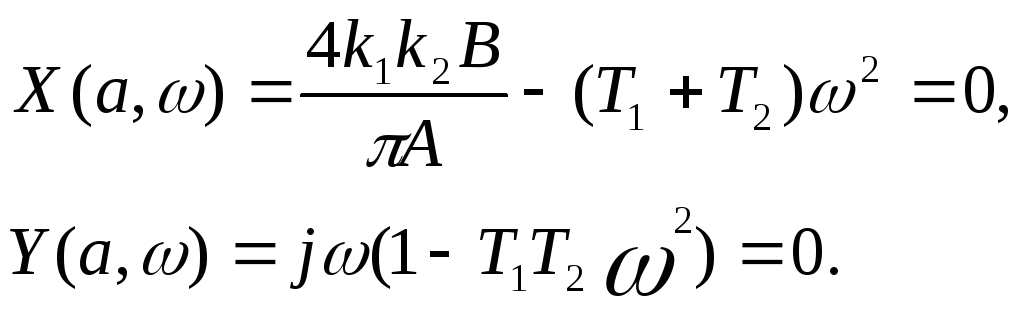(3.22)

Из второго уравнения определяем частоту периодического решения

,

а из первого при этом получаем

. (3.23)

Используя готовый график q(а)= (рисунок 3.5), находим амплитуду периодического решения а.

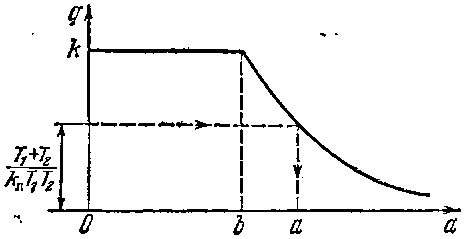
Рисунок 3.5 – График функции q(a)

Для определения устойчивости решения, согласно критерию, надо найти производные выражений (3.22):

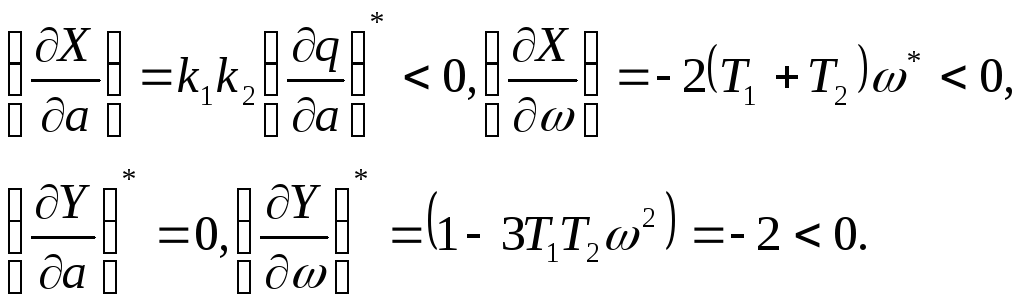
Критерий удовлетворяется. Следовательно, имеют место автоколебания.

Если учесть, что q(а)=<k (см.рисунок 3.5), из уравнения (3.23) вытекают условия существования автоколебаний

или (3.24)

где К = k₁k₂k— общий коэффициент усиления разомкнутой цепи данной системы в линейном плане. Легко видеть, что (3.24) представляет собой условие неустойчивости этой системы как линейной согласно критерию Гурвица. Граница устойчивости

является в то же время границей автоколебаний.