
- •1 Лабораторная работа №1. Изучение фазовых портретов линейных систем второго порядка
- •1.2 Задание на лабораторную работу
- •1.3 Требования к отчету по работе
- •1.4 Контрольные вопросы
- •2 Лабораторная работа №2 Исследование систем с переменной структурой
- •2.2 Задание на лабораторную работу
- •2.3 Требования к отчету
- •3 Лабораторная работа №3. Исследования автоколебаний в нелинейной системе методом гармонического баланса
- •3.1 Общие сведения
- •3.2 Задание на выполнение лабораторной работы
- •3.3 Требования к отчету
- •4. Список литературы
1.2 Задание на лабораторную работу
1.2.1 Подберите значенеия параметров системы для различных вариантов корней храктеристического уравнения (для приведенных случаев).
1.2.2 Для различных начальных значений х0 и х00 определите переходные характеристики и фазовые траектории.
1.2.3 Выполните следующие задания в среде VisSim:
- для уравнений (1.1), (1.2) постройте структурную схема решения;
- выберите
значения a
0,
a1,
a2
для первого случая, определите
![]() и
и![]() ,
установите на схеме оэффициентыk1
жәине
k2;
,
установите на схеме оэффициентыk1
жәине
k2;
- для различных начальных условий получите переходные процессы х1 и определите значение коэффициента для времени tпп переходного процесса;
- используя координаты х1 и х2=х1, определите фазовые траектории системы;
1.2.4 Выполните задания предыдущих пунктов для всех (2, 3, 4, 5, 6) случаев.
1.3 Требования к отчету по работе
Отчет по работе должен содержать:
- схему системы;
- выбранные значения коэффициентов;
- корни характеристического уравнения;
- график переходного процесса;
- график фазовой траектории.
1.4 Контрольные вопросы
1.4.1 Объсните суть фазового метода.
1.4.2 Какая существует взаимосвязь между корнями характеристического уравнения и фазовыми портретами линейных систем второго порядка?
1.4.3 Как будет выглядеть фазовая координата устойчивой системы?
1.4.4 Как будет выглядеть фазовая координата, если в системе есть затухающий колебательный процесс?
1.4.5 Как будет выглядеть фазовая координата, если в системе есть незатухающие колебания?
1.4.6 Как будет выглядеть фазовая координата, если имеет место бесконечное возрастание выходной величины?
2 Лабораторная работа №2 Исследование систем с переменной структурой
Цель работы: построение и исследование фазовых портретов нелинейных систем 2-го порядка с переменной структурой.
Исследование переходных характеристик и фазовых портретов систем второго порядка в предыдущей лабораторной работе показывает, что имеются решения с неустойчивым движением. На практике могут оказаться случаи, когда невозможно получить устойчивую систему при определенных значениях параметров объекта управления. В то же время можно исследовать метод припасовывания для построения фазовых портретов нелинейных систем, допускающих кусочно-линейную аппроксимацию характеристик. Согласно этому методу, фазовую траекторию строят по частям, каждой из которых соответствуют линейные участки характеристик, причем значения фазовых координат в конце каждого участка фазовой траектории являются начальными условиями для решения уравнения на следующем участке. Общий фазовый портрет системы получают «сшиванием» фазовых траекторий, найденных на отдельных участках.
В данной работе требуется построить фазовый портрет замкнутой нелинейной системы состоящей из линейной части и нелинейного элемента, осуществляющего переключения структуры при заданном алгоритме управления (см.рисунок 2.1).
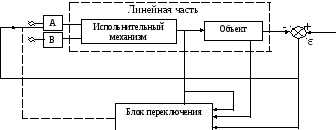
Рисунок 2.1 – Схема замкнутой нелинейной системы
Метод припасовывания лежит в основе построения систем с переменной структурой, дает дополнительную возможность получения различных желаемых процессов автоматического регулирования.
Рассмотрим переходной процесс системы, где исполнительный механизм вместе с регулируемым объектом описываются передаточной функцией
![]() .
(2.1)
.
(2.1)
Первое и второе звенья характеризуется коэффициентами усиления k1 и k2 соответственно. Тогда уравнения динамики замкнутой системы будут
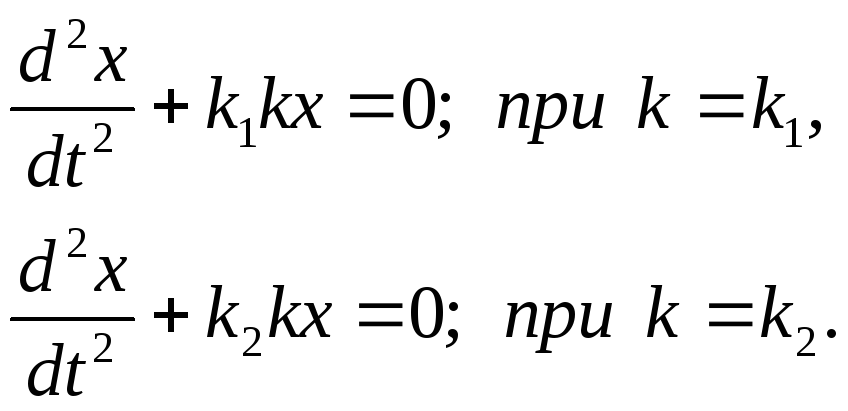
К аждое
из этих уравнений является уравнением
неустойчивой системы (незатухающие
колебания). Фазовые портреты системы
будут как на рисунках(2.2а)
и (2.3б).
аждое
из этих уравнений является уравнением
неустойчивой системы (незатухающие
колебания). Фазовые портреты системы
будут как на рисунках(2.2а)
и (2.3б).
Рисунок 2.2–
Фазовые портреты системы
Обозначим
![]() .
.
Ведем следующий закон переключений:
![]() ,
(2.4)
,
(2.4)
![]() .
(2.5)
.
(2.5)
Если следовать законам переключения (2.4) и (2.5) и использовать метод припасовывания, то получим затухающий колебательный процесс, т.е. за счет переменности структуры система становится устойчивой (см.рисунок 2.3).

Рисунок 2.3 – Устойчивая система
Рассмотрим следующее уравнение системы второго порядка
![]() ,
(2.6)
,
(2.6)
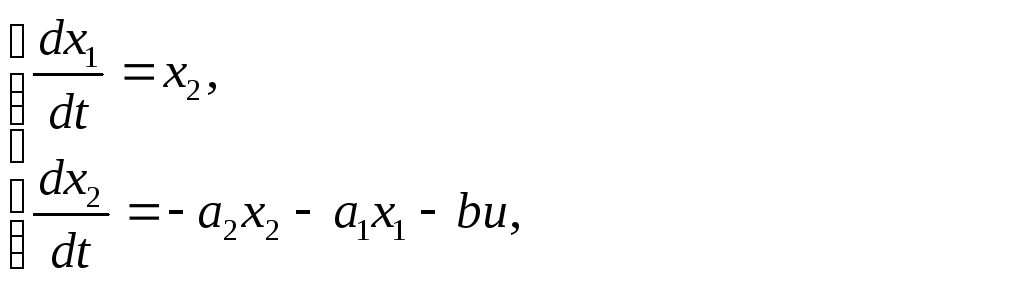
(2.7)
(2.8)
![]() ,
,
![]() ,
(2.9)
,
(2.9)
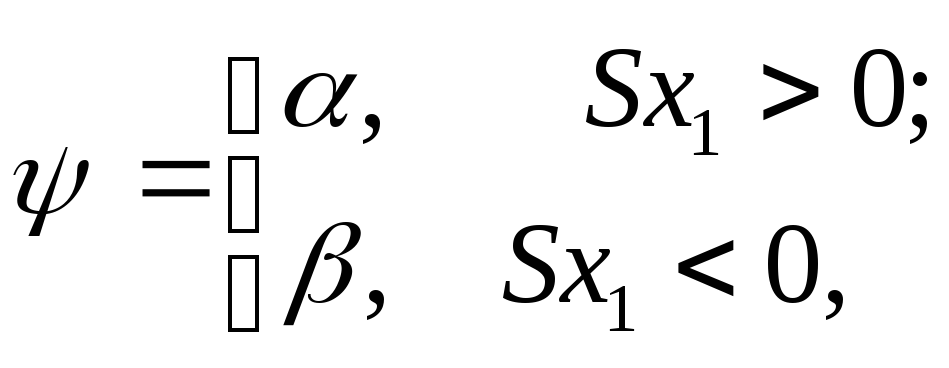 (2.10)
(2.10)
![]() и
и
![]() .
.
Тогда фазовые траектории будут как на рисунке 2.4а и 2.4б.
Из следующего соотношения
![]() ,
(2.11)
,
(2.11)
здесь λ1,2 – корни уравнения (2.8), получим
S=x2-cx1 , (2.12)
S – одна из линий переключения. Из уравнения (2.10) видно, что линиями переключения является прямая S и ось абсцисс х1=0.
В работе надо исследовать три разлияных режима:
режим преключений (с>λ); здесь фазовый портрет будет выглядеть как на рисунке 2.5;

Рисунок 2.4– Фазовые траектории системы второго порядка
2) режим движения по вырожденным траекториям; в данном случае линия переключения S совпадает совпадает с асимптотой (устойчивой) S1 .

Рисунок 2.5– Фазовые портреты режима переключения
Изображающая, начинаясь с любой точки фазовой плоскости, попадает на линию переключения S, затем продолжает движение к началу координат по устойчивой асимптоте. При этом получаем переходной процесс максимум с одним перерегулированием (рисунок 2.6);

Рисунок 2.6 – Режим движения по заданной траектории
3) режим «скольжения» - наиболее интересный и полезный случай, когда с<λ. Особенностью является то, что фазовые портреты направлены навстречу друг другу на линии переключения S. В идеальном варианте изображаемая точка на пути S переключается с бесконечной частотой. И так как регулирующий вектор направлен в сторону начала координат, она устремляется к нулю вдоль линии переключения (см.рисунок 2.7).

Рисунок 2.7 - Реализация устойчивых движений с помощью системы с переменной структурой
