1 Лабораторная работа №1. Изучение фазовых портретов линейных систем второго порядка

Цель работы: знакомство с одним из методов исследования нелинейных систем - методом фазовой плоскости; исследование взаимосвязей между корнями характеристического уравнения переходного процесса и фазовыми портретами линейных систем второго порядка.

1. Общие сведения

Метод фазового пространства применим для исследования как линейных, так и нелинейных систем. Наиболее наглядное представление дает рассмотрение линейной системы, описываемой дифференциальным уравнением второго порядка.

(1.1)

где х - отклонение регулируемой (выходной) координаты системы от состояния равновесия.

Введем фазовые координаты и перепишем уравнение (1.1) в следующем виде:

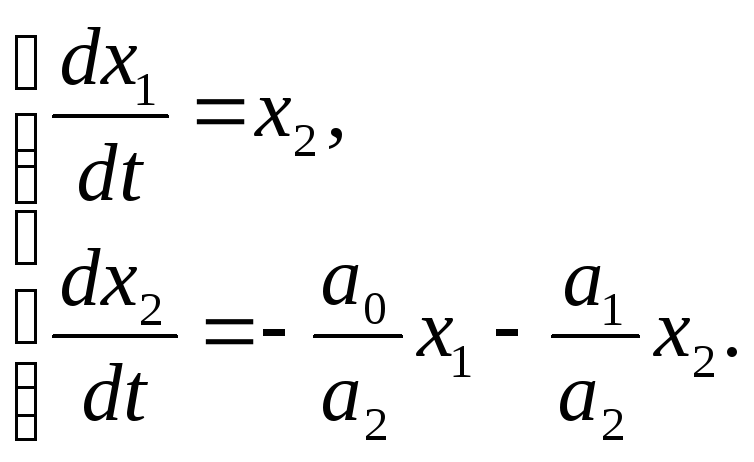(1.2)

Очевидно, что в плоскости (х₁, х₂) состоянию равновесия системы будет соответствовать начало координат.

Интегрирование уравнений (1.2) дает уравнения кривых, по которым строят фазовые траектории.

. (1.3)

Конкретный вид функции зависит от коэффициентов . Но так как эти же коэффициенты определяют и корни характеристического уравнения данной системы

, (1.4)

то существует однозначная зависимость между корнями и типом фазового портрета линейной системы 2-го порядка.

При этом возможны шесть различных случаев:

1. корни вещественные и отрицательные

-

система устойчивая;

2) корни комплексные и имеют отрицательные вещественные части

- система устойчивая;

3) корни чисто мнимые

- колебательная граница устойчивости линейной системы;

4) корни комплексные и имеют положительные вещественные части

- неустойчивая линейная система;

5) корни вещественные положительные

- неустойчивая линейная система;

6) корни вещественные и имеют разные знаки

- система неустойчивая.

Рассмотрим эти ситуации:

1) в системе есть апериодический затухающий переходной процесс и уравнение (1.1) имеет решение

(1.5)

Вторая фазовая координата по времени будет иметь вид

. (1.6)

На фазоворй плоскости все координаты пересекаются в начале координат и имеются следующие две асимптоты

и ; (1.7)

2. имеется затухающий колебательный процесс

, (1.8)

, (1.9)

, (1.10)

. (1.11)

Уравнения (1.8), (1.10) на фазовой плоскости дают семейство спиралей.

3) имеется следующее решение

, (1.12)

, то есть присутствуют незатухающие колебания

Вторая фазовая координата будет иметь вид

. (1.13)

Для фазовой траектории уравнение будет иметь вид

, (1.14)

то есть фазовые плоскости являются эллипсами.

4) решение уравнения имеет вид:

, (1.15)

,

то есть имеют место колебания с бесконечно возрастающей амплитудой. Фазовая траектория – плоская расходящаяся спираль;

5) решение уравнения имеет вид:

, (1.16)

, (1.17)

то есть имеет место бесконечное возрастание выходной величины. На фазовой плоскости появятся две асимптоты

и (1.18)

6) переходная характеристика будет апериордической, но фазовая траектория другая. Например, а₁=0. Тогда уравнение (1.2) запишется в следующем виде

(1.19)

или

(1.20)

Если проинтегрируем уравнение (1.20), получим фазовые траектории в виде гипербол

. (1.21)

Асимптотами гипербол являются прямые , здесь .