Энергия магнитного поля и расчет индуктивности проводников

Краткие теоретические сведения

Учитывая симметричность понятий электрического и магнитного поля, выражение для энергии последнего принимает вид

. (8.1)

Осуществляя переход от энергии магнитного поля к энергии проводника с током, получим выражение

, (8.2)

где – индуктивность (коэффициент самоиндукции) проводника.

Рассматривая два контура с током рассчитаем поток вектора магнитной индукции через поверхность первого из них. Получим следующее выражение –

, (8.3)

где и– токи в первом и втором контуре,– коэффициент взаимной индукции,– коэффициент самоиндукции первого контура.

Исходя из определения потока и понятия векторного потенциала, для коэффициента индукции получим общее выражение

. (8.4)

Соответственно для коэффициента самоиндукции –

. (8.5)

В случае рассмотрения линейных проводников удобно осуществить формальный переход

. (8.6)

Коэффициенты индукции и самоиндукции зависят лишь от формы контуров их взаимного расположения, и не зависят от токов, которые по ним протекают.

В дальнейшем, говоря об индуктивности проводника, мы будем иметь в виду коэффициент самоиндукции. В остальных случаях удобно использовать термин «коэффициент индукции».

Темы для развернутых ответов

1. Энергия магнитного поля и проводника с током.

2. Индуктивность проводника.

Литература:[1], глава 8, §47; [3], глава 4, §52.

Основной блок задач

1. Рассчитайте энергию и индуктивность соленоида, имеющего 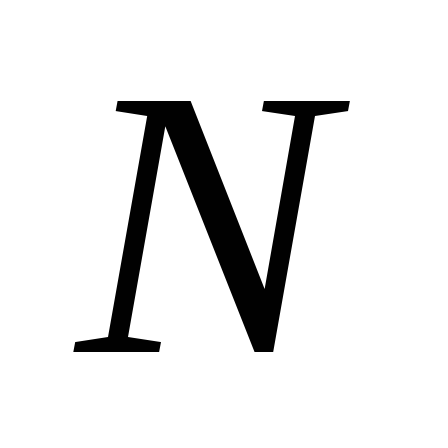витков, длину, сердечник с магнитной проницаемостью. По соленоиду течет ток, а площадь сечения витка.

2. Линия состоит из двух коаксиальных тонких цилиндрических оболочек с радиусами и(), пространство между ними заполнено веществом с магнитной проницаемостью. Найдите индуктивность единицы длины данной линии.

3. Определите индуктивность единицы длины двухпроводной линии. Линия состоит из двух параллельных прямых проводов, радиусы которых и, расстояние между осевыми линиями. По проводам текут равные по величине, но противоположные по направлению токи.

Дополнительный блок задач

4. Определите индуктивность тонкого проволочного кольца радиуса . Радиус провода.

5. Найдите индуктивность единицы длины бесконечного цилиндрического соленоида с густой намоткой и с произвольной формой сечения. Площадь сечения , число витков на единицу длины.

6. Длинный прямой провод и кольцо радиуса лежат в одной плоскости. Расстояние от центра кольца до провода. Найдите коэффициент взаимной индукции, если сила тока в проводниках равна соответственнои.

Практическое занятие №9

Законы Ома и Джоуля-Ленца

Краткие теоретические сведения

На основе экспериментально открытого Г.С. Омом закона, связывающего ток в проводнике с приложенной к нему разностью потенциалов (закон Ома для однородного участка цепи)

(9.1)

запишем его дифференциальную форму для плотности тока. Учтем, что удельное сопротивление проводника связано с его проводимостьюкак

. (9.2)

Запись закона Ома для однородного участка цепи имеет вид

, (9.3)

для неоднородного –

, (9.4)

где – плотность тока.

Закон Джоуля-Ленца в дифференциальной форме связывает тепловую мощность, выделяемую в единице объема проводника с плотностью тока и напряженностью электрического поля –

. (9.5)

Темы для развернутых ответов

1. Закон Ома в дифференциальной и интегральной формах.

2. Закон Джоуля-Ленца в дифференциальной и интегральной формах.

Литература:[1], глава 2, §16, глава 4, §26-27; [3], глава 3, §35-38.

Основной блок задач

1. Найти сопротивление среды току между двумя концентрическими электродами радиусами и(). Удельная проводимость среды равна.

2. Между двумя плоскими электродами площади каждый, линейные размеры которых много больше расстояниямежду ними, находится проводящий материал, удельная проводимость которого изменяется линейно отдоу разных поверхностей. Найдите сопротивление среды между электродами.

3. Найдите сопротивление конического проводника кругового сечения, основания которого имеют радиусы и. Проводимость среды равна.

4. Полусферический заземлитель погружен в землю вровень с ее поверхностью. Найти напряжение, под которым может оказаться человек, приближающийся к заземлителю (шаговое напряжение). Сила тока , протекающего через заземлитель, задана. Длина шага равна, расстояние от ближней к заземлителю ноги человека до него равно. Рассчитайте шаговое напряжение при условии, что,,,.

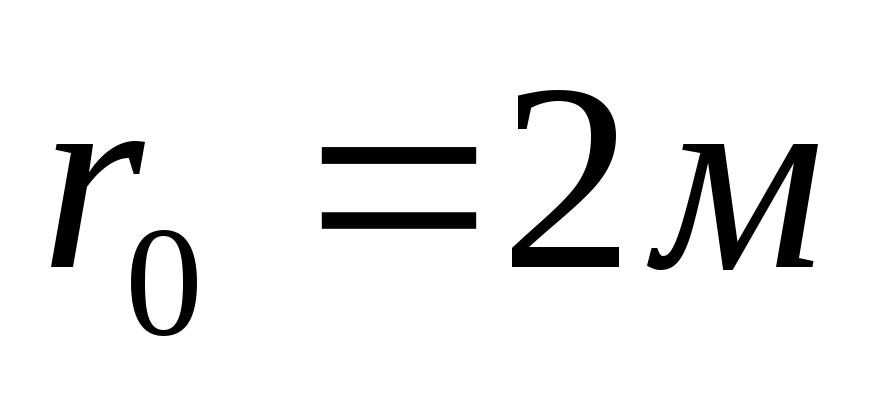Дополнительный блок задач

5. Длинный проводник круглого сечения радиуса сделан из материала, удельное сопротивление которого зависит только от расстояниядо оси проводника по закону. Найдите сопротивление единицы длины проводника и напряженность электрического поля, если по проводнику течет ток. Какая мощность выделяется в проводнике?

6. Провод длиной , по которому течет ток, упал со столба на землю. Найти шаговое напряжение, если известно, что длина шага, расстояние от провода до ближайшей ноги. Найдите ответ, учитывая следующие данные:,,,.

Практическое занятие №12