
- •А.В. Дюндин
- •Введение
- •Расчет напряженности электрического поля
- •Потенциал электрического поля
- •Прямая и обратная задачи электростатики
- •Энергия заряженного тела и электрического поля
- •Емкость уединенного проводника и системы проводников
- •Расчет индукции магнитного поля
- •Расчет магнитных полей с помощью векторного потенциала Решение прямой и обратной задач магнитостатики
- •Закон электромагнитной индукции Фарадея
- •Энергия магнитного поля и расчет индуктивности проводников
- •Законы Ома и Джоуля-Ленца
- •Квазистационарные явления в электрических цепях
- •Переменное электромагнитное поле
- •Электромагнитные волны
- •Основы специальной теории относительности
- •Основы релятивистской динамики
- •Пространство Минковского и четырехмерные векторы
- •Элементы релятивистской электродинамики
- •Математические основы электродинамики
Прямая и обратная задачи электростатики
Теория
Решая совместно уравнения Максвелла
![]() и
и![]() в
электростатическом случае получают
уравнение Пуассона, которое описывает
связь потенциала электрического поля
с распределением зарядов, то есть
связывает полевые характеристики
(потенциал) со свойствами среды (объемная
плотность заряда)
в
электростатическом случае получают
уравнение Пуассона, которое описывает
связь потенциала электрического поля
с распределением зарядов, то есть
связывает полевые характеристики
(потенциал) со свойствами среды (объемная
плотность заряда)
![]() .
(3.1)
.
(3.1)
Если в данной точке среды отсутствуют объемные заряды, то получаем частный случай уравнения Пуассона – уравнение Лапласа
![]() .
(3.2)
.
(3.2)
Оператор
![]() – оператор Лапласа, выражение для
которого зависит от системы координат.
– оператор Лапласа, выражение для
которого зависит от системы координат.
В декартовой системе координат
![]() ;
(3.3)
в цилиндрической –
;
(3.3)
в цилиндрической –
![]() ;
(3.4)
в сферической –
;
(3.4)
в сферической –
![]() .(3.5)
.(3.5)
В случае распределения заряда по сфере, шару или цилиндру в силу симметрии запись оператора Лапласа можно сократить:
![]() ,
(3.6)
,
(3.6)
![]() .
(3.7)
.
(3.7)
Прямой задачей электростатики называют нахождение потенциала электрического поля по известному распределению заряда
![]() ,
(3.8)
,
(3.8)
а обратной – нахождение распределения зарядов по известному потенциалу
![]() .
(3.9)
.
(3.9)
Темы для развернутых ответов
Прямая и обратная задачи электростатики. Примеры.
Уравнение Пуассона и его решение. Привести пример.
Алгоритм решения прямой задачи электростатики (решения уравнения Пуассона):
По условию задачи найти
 в заданной точке наблюдения. Записать
уравнение Пуассона или Лапласа (
в заданной точке наблюдения. Записать
уравнение Пуассона или Лапласа ( )
в инвариантной форме.
)
в инвариантной форме.Исходя из симметрии задачи выбирать систему координат так, чтобы потенциал (по возможности) зависел от одной переменной.
Решить дифференциальное уравнение второго порядка. В решение войдут произвольные константы.
Найти значения констант из условий, которым должен соответствовать потенциал – непрерывность и конечность, также используя граничные условия для вектора напряженности электрического поля (если есть граница раздела сред).
Для использования граничных условий необходимо повторить пункты с 1 по 3 для второй среды, получив еще две константы.
Литература:[1], глава 2, §15; [3], глава 1, §11.
Основной блок задач
Дан шар радиуса
 ,
равномерно заряженный по объему с
плотностью заряда
,
равномерно заряженный по объему с
плотностью заряда .
Вычислить потенциал, создаваемый шаром
в точке наблюдения
.
Вычислить потенциал, создаваемый шаром
в точке наблюдения при условии:
при условии:
а) точка
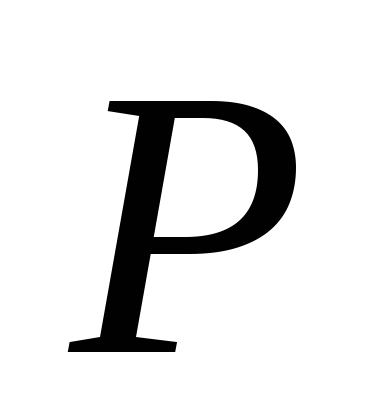 лежит вне шара
лежит вне шара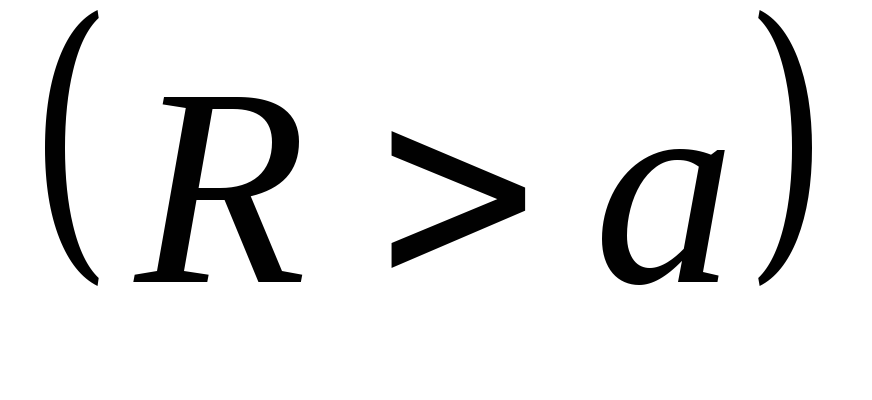 ;
;б) точка
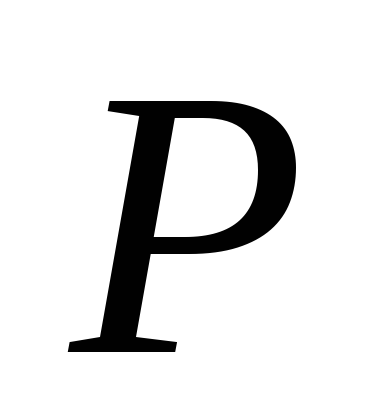 лежит внутри шара
лежит внутри шара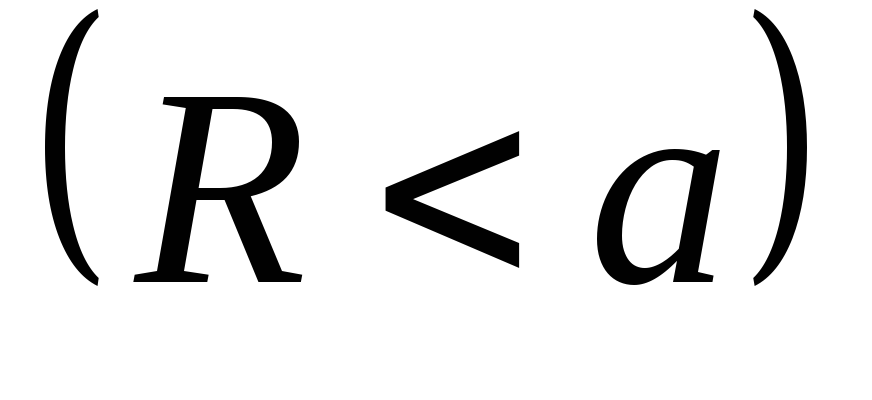 .
.
Рассчитайте потенциал, создаваемый
бесконечно длинным цилиндром радиуса
![]() ,
заряженного по объему с плотностью
,
заряженного по объему с плотностью![]() .
.
Дана бесконечная пластинка, ориентированная
в пространстве перпендикулярно оси
![]() .
Толщина пластинки
.
Толщина пластинки![]() ,
она заряжена с объемной плотностью
заряда
,
она заряжена с объемной плотностью
заряда![]() .
Точка наблюдения находится на расстоянии
.
Точка наблюдения находится на расстоянии![]() от центра пластины. Найдите потенциал
электрического поля в точке наблюдения.
от центра пластины. Найдите потенциал
электрического поля в точке наблюдения.
Дополнительный блок задач
В сферических координатах объемная плотность заряда внутри шара радиуса
 симметрична относительно оси
симметрична относительно оси и имеет вид
и имеет вид ,
где
,
где – полярный угол, а начало координат
совпадает с центром шара. Найдите
потенциал и напряженность электрического
поля, создаваемого этим шаром, во всем
пространстве. Учтите, что в данном
случае потенциал не зависит от
азимутального угла
– полярный угол, а начало координат
совпадает с центром шара. Найдите
потенциал и напряженность электрического
поля, создаваемого этим шаром, во всем
пространстве. Учтите, что в данном
случае потенциал не зависит от
азимутального угла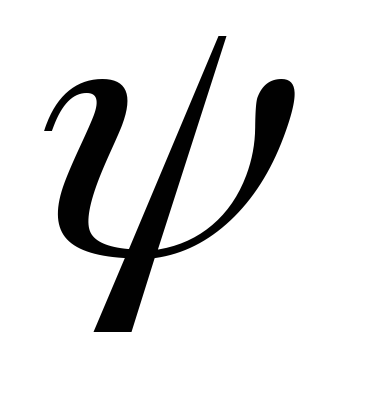 .
.Бесконечный цилиндр радиуса
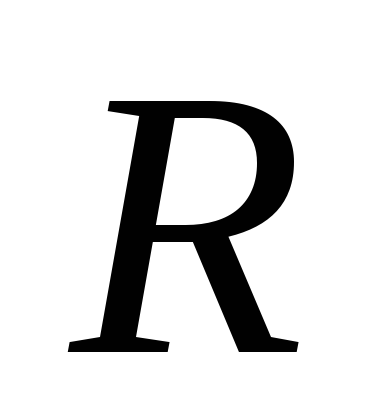 заряжен равномерно по своей длине.
Объемная плотность заряда
заряжен равномерно по своей длине.
Объемная плотность заряда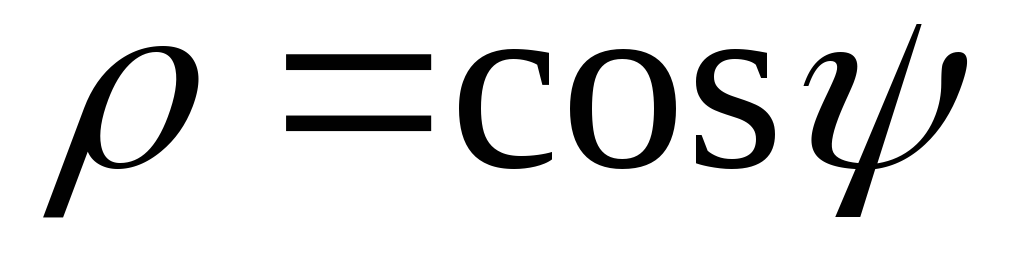 ,
где
,
где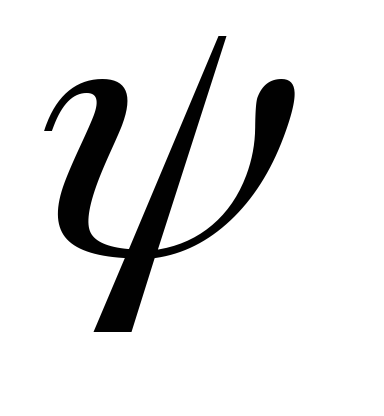 – полярный угол, а ось
– полярный угол, а ось цилиндрической системы координат
совпадает с осью цилиндра. Найдите
потенциал и напряженность электрического
поля, создаваемого этим цилиндром, во
всем пространстве.
цилиндрической системы координат
совпадает с осью цилиндра. Найдите
потенциал и напряженность электрического
поля, создаваемого этим цилиндром, во
всем пространстве.Найдите распределение объемной плотности
 заряда, создавшего в пространстве
электрическое поле, потенциал которого
в сферических координатах имеет вид:
заряда, создавшего в пространстве
электрическое поле, потенциал которого
в сферических координатах имеет вид:
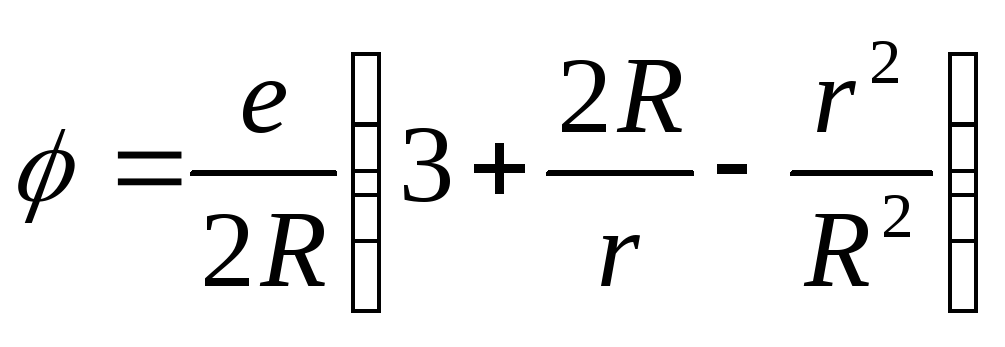 при
при ;
;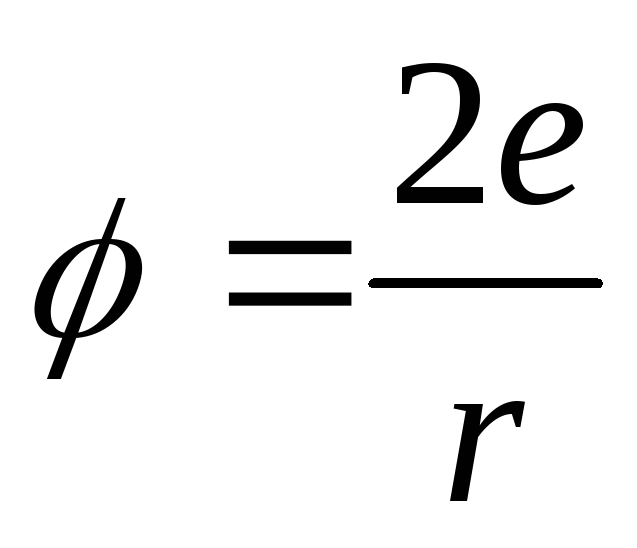 при
при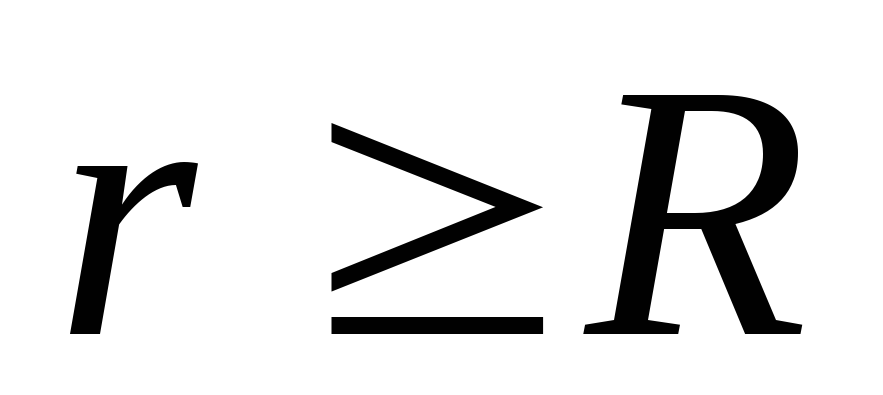 ;
где
;
где и
и – некоторые постоянные.
– некоторые постоянные.
Потенциал
![]() электрического поля в сферических
координатах имеет вид
электрического поля в сферических
координатах имеет вид![]() при
при![]() и
и![]() при
при![]() ,
где
,
где![]() и
и![]() – постоянные. Найдите распределение
заряда, создавшего это поле
– постоянные. Найдите распределение
заряда, создавшего это поле
Замечание: Условия упражнений 4-7 записаны в системе СГСЭ, однако методы решения остаются теми же.
Практическое занятие №4
