
Определение ускорения свободного падения при помощи математического маятника
Учебно-методическое пособие
к лабораторной работе № 1.1
Владивосток
2013
УДК53(076.5)
ББК 22.36
О-60
О-60 Определение ускорения свободного падения при помощи математического маятника: учебно-методич. пособие к лабораторной работе № 1.1 по дисциплине «физический практикум»/ /
сост. В.Е. Полищук, Р.Ф. Полищук. - Владивосток : Издательский дом Дальневост.федерал. ун-та, 2013.-11 с.
Пособие, подготовленное на кафедре общей физики Школы естественных наук ДВФУ, содержит методические указания к выполнению лабораторной работы по механике с целью экспериментального изучения применения математического маятника для измерения ускорения свободного падения.
Для студентов школы естественных наук, обучающихся по специальности 11200.62 - «физика».
УДК 53(076.5)
ББК 22.36
© Полищук В.Е.
Полищук Р.Ф.
составление, 2013
Учебное издание
Определение ускорения свободного падения
При помощи математического маятника
Учебно-методическое пособие
к лабораторной работе № 1.1
Составители
Полищук Виталий Ефремович
Полищук Раиса Федоровна
В авторской редакции
Компьютерный набор и верстка В.Е. Полищук
Формат 60х84 1/16
Усл. печ. л. 0,70. Уч.-изд.л. 0,75. Тираж 100 экз.
Издательский дом Дальневосточного федерального университета
690950, Владивосток, Октябрьская, 27.
Отпечатано на кафедре общей физики ШЕН ДВФУ
690950, Владивосток, ул. Суханова, 8.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«Дальневосточный федеральный университет»
(ДВФУ)
Школа естественных наук
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ ПРИ ПОМОЩИ МАТЕМАТИЧЕСКОГО МАЯТНИКА
Учебно-методическое пособие
к лабораторной работе № 1.1
по дисциплине «физический практикум»
11200.62 - «физика»
Владивосток
Издательский дом Дальневосточного федерального университета
2013
Цель данной работы – изучить законы колебаний математического маятника и ознакомиться с методикой экспериментального определения ускорения свободного падения с его помощью.
Краткая теория. Механическое движение тел – изменение их положения в пространстве с течением времени. Движение тела подразделяется на три вида:
поступательное– все точки тела движутся одинаково (скорость и ускорение всех точек тела одинаковы и по величине и по направлению);
вращательное– все точки тела движутся по окружностям вокруг общего центра или оси;
колебательное – все точки тела
совершают возвратно-поступательное
или возвратно-вращательное движение.
При линейном колебательном движении
точка М не выходит за пределы какого-либо
отрезкаKLна этой линии
и многократно проходит через одни и те
же положения внутри этого отрезка
(Рис.1). Колебательное движение
характеризуется определенной
повторяемостью во времени. Если при
таком движении существует определенный
промежуток времени Т, через который
движение точки М в точности повторяется,
то такое колебание называетсяпериодическим.
Существует множество различных видов периодических колебаний, простейшими из которых являются гармонические колебания– колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Гармонические колебания – это идеализация, занимающая среди всех других колебаний особое место, что обусловлено двумя причинами:
1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническим колебаниям;
2) любое негармоническое колебание можно представить в виде суммы (наложений) различных гармонических колебаний.
Кинематическое уравнение гармонических колебаний имеет вид
X= A Sin(ωt+φо) (1) или X= A Cos(ωt+φо). (2).
В уравнениях (1) и (2):
Х–смещение (отклонение) колеблющейся точки от положения равновесия в момент времениt;
А–амплитудаколебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия(А = |Хmax|).Амплитуда и смещение в системе СИ измеряются в метрах.
ω–циклическая частота, величина, показывающая число полных колебаний, происходящих в течение2πсекунд. В системе СИ циклическая частота измеряется в с-1. Циклическая частота связана с периодом колебанийТи частотойν.
Т–период колебаний, величина,
определяющая время одного полного
колебания (промежуток времени между
двумя последовательными прохождениями
колеблющейся точки через одно и то же
положение в одном и том же направлении).Т=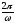 ,
илиω=
,
илиω=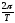 .Период в системе СИ измеряется в секундах.
.Период в системе СИ измеряется в секундах.
ν –частота колебаний, величина,
показывающая число полных колебаний
за единицу времени.Частота связана
с периодом и циклической частотой
соотношениями: ν =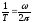 .В системе СИ частота ν измеряется в
герцах (герц- одно колебание за секунду).
.В системе СИ частота ν измеряется в
герцах (герц- одно колебание за секунду).
ωt+φо –фаза колебаний,величина, определяющая величину смещенияХколеблющейся точки от положения равновесия в данный момент времениt.
φо – начальная фаза, величина, определяющая величину смещения Х колеблющейся точки от положения равновесия в начальный момент времени (t=0). Начальная фаза и фаза колебаний измеряются в угловых единицах, т.е. в градусах или в радианах (в долях π).
Используя одно из кинематических уравнений гармонических колебаний, например уравнение (1), найдем кинематические характеристики этих колебаний – скорость и ускорение.
Скорость V – это первая производная по времени от смещения Х:
V
=
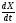 =AωCos(ωt+
φо),
(3)
=AωCos(ωt+
φо),
(3)
где величина Aω– амплитуда скорости Аvгармонических колебаний.
Ускорение гармонических колебаний αопределится как первая производная по времени от скорости гармонических колебаний, или вторая производная по времени от смещения
 α
=
α
=
 =
=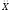 = - Аω2Sin(ωt+
φо),
(4)
= - Аω2Sin(ωt+
φо),
(4)
где величина А
ω2
– амплитуда ускорения Аα.
С учетом уравнения (1), ускорение
гармонических колебаний (уравнение
(4)) можно представить в другом виде: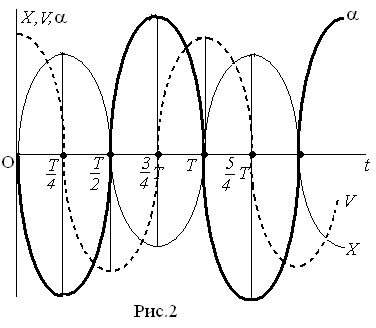
α=-ω2АSin(ωt+ φо)=-ω2Х (5)
Из формул (1), (2) и (3) видно, что при
гармонических колебаниях смещение,скорость и ускорение характеризуются
одинаковой циклической частотой и,
следовательно периодом (Т= ).
Фазы колебаний указанных величин
различны: колебание скорости опережает
колебание смещения по фазе на
).
Фазы колебаний указанных величин
различны: колебание скорости опережает
колебание смещения по фазе на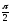 (по времени на
(по времени на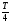 ),
колебание ускорения опережает колебание
смещения по фазе на π, (по времени на
),
колебание ускорения опережает колебание
смещения по фазе на π, (по времени на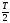 ).
).
На рисунке 2 представлены графики зависимости от времени смещения, скорости и ускорения (начальная фаза φо=0). Как видно из рисунка, в момент прохождения колеблющейся точкой положения равновесия (Х=0) ее скорость максимальна. Когда же точка максимально отклонится от положения равновесия (Х=+АилиХ=-А), ее скорость равна нулю, а ускорение становится максимальным. При этом, знак ускорения всегда противоположен знаку смещения, т.е. ускорение всегда направлено к положению равновесия колеблющейся точки.
Зная массу mколеблющейся частицы (материальная точка) и ее ускорение, определяемое уравнением (5), найдем силу, под действием которой совершаются гармонические колеба- ния. Согласно второму закону Ньютона эта сила равна
F = mα = -m ω2Х = - kX, (6)
где k = m ω2- коэффициент пропорциональности является постоянной величиной для данного осциллятора (осциллятор - физическая система, совершающая колебания). Из уравнения (6) видно, что сила, вызывающая гармоническое колебание, пропорциональна смещениюХи направлена против смещения, на что указывает знак минус. Эта сила стремится возвратить колеблющуюся точку в положение равновесия, поэтому ее называютвозвращающей силой. Такой силой, например, может бытьсила упругости, возникающая при малых деформациях любого вида, которая, согласно закону Гука, пропорциональна деформации (смещению)∆Хи противоположна ему по знаку. Возвращающие силы могут иметь и иную,не упругуюприроду. В этих случаях они называютсяквазиупругими силами (т.е. «как бы подобны упругим силам»). Коэффициентk, определяющий значение силы, вызывающей смещение, называют коэффициентом возвращающей силы. Как силы упругости, так и квазиупругие силы являются внутренними силами колеблющейся системы. Следовательно.гармонические колебания происходят под действием внутренних упругих, или на них похожих, квазиупругих сил. Колебания, происходящие только под действием внутренних сил, называютсясвободными (или собственными).
Энергия гармонических колебаний. Для гармонических колебаний выполняется закон сохранения механической энергии, согласно которого полная энергия Егармонического осциллятора остается постоянной. Докажем это утверждение. Полная механическая энергияЕскладывается из кинетическойEkи потенциальнойEpэнергий
Е = Ek + Ep (7)
Кинетическая энергия является мерой движения и для материальной точки (или поступательного движения твердого тела) определяется по формуле
Ek
=
 ,(8)
,(8)
где m– масса колеблющейся точки,V– скорость ее движения.
Потенциальная энергия определяется состоянием тела или его положением в пространстве. Для упругих (или квазиупругих) сил потенциальная энергия тела определяется по формуле
Ep
=
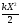 ,(9)
,(9)
где k– коэффициент упругости,Х – смещение колеблющейся точки от положения равновесия.
Подставив уравнения (1) и (3) соответственно в уравнения (9) и (8) и, используя соотношение k = m ω2, а также то, что суммаCos2(ωt + φo) + Sin2(ωt + φo) = 1, получим
выражение для полной механической энергии гармонических колебаний:
Е =
 +
+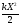 =
= +
+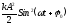 =
=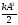 (10)
(10)
Величины, стоящие в уравнении
справа (k и А) –
постоянные для данного гармонического
осциллятора и, следовательно, полная
энергия гармонических колебанийЕ
для данного осциллятора есть величина
постоянная. При этом, как кинетическая,
так и потенциальная энергии, изменяются
в противофазах, соответственно, по
квадратичным законам косинуса и синуса
(рис. 3).
Математический
маятник, период его колебаний. Примером
механических гармонических колебаний
под действием квазиупругих сил является
колебание математического маятника.
Математическим маятником называют
идеализированную систему, состоящую
из невесомой и нерастяжимой нити, на
которой подвешена масса, сосредоточенная
в одной точке. Достаточно хорошим
приближением к математическому маятнику
служит небольшой тяжелый шарик,
подвешенный на длинной тонкой нерастяжимой
нити (рис.4). На шарик маятника всегда
действуют две силы: сила тяжести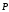 и сила натяжения нити
и сила натяжения нити .
В положении равновесия (свободно висящий
маятник) сумма указанных сил равна нулю.
На шарик маятника, отклонённого от
положения равновесия на уголφ,
будет действовать возвращающая сила
.
В положении равновесия (свободно висящий
маятник) сумма указанных сил равна нулю.
На шарик маятника, отклонённого от
положения равновесия на уголφ,
будет действовать возвращающая сила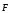 ,
равная результирующей двух сил: силы
тяжести
,
равная результирующей двух сил: силы
тяжести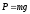 (g–ускорение свободного
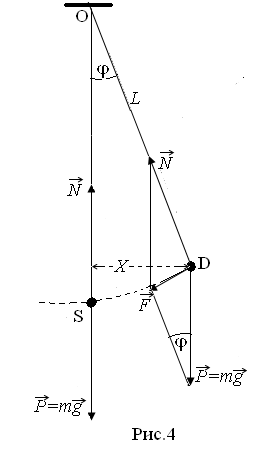
падения) и силы натяжения нити
(g–ускорение свободного
падения) и силы натяжения нити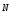 .
.
Под действием этой
возвращающей силы
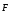 ,
маятник начнет ускоренно двигаться от
точкиD
к точке S
(положению равновесия). В точке S
величина силы
,
маятник начнет ускоренно двигаться от
точкиD
к точке S
(положению равновесия). В точке S
величина силы
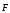 равна нулю, но так как маятник обладает
массой m
и к моменту прохождения точки S
имеет скорость V,
то он по инерции пройдет эту точку. При
дальнейшем движении маятника по дуге
его скорость будет понижаться вследствие
того, что направление силы
равна нулю, но так как маятник обладает
массой m
и к моменту прохождения точки S
имеет скорость V,
то он по инерции пройдет эту точку. При
дальнейшем движении маятника по дуге
его скорость будет понижаться вследствие
того, что направление силы
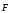 изменится
и будет противоположно направлению
движения маятника. В конечной точке
движения маятник остановится и сразу
же начнет движение к точке S.
Таким образом, маятник будет совершать
под действием силы
изменится
и будет противоположно направлению
движения маятника. В конечной точке
движения маятник остановится и сразу
же начнет движение к точке S.
Таким образом, маятник будет совершать
под действием силы
 колебательные движения. Если на маятник
не действуют силы трения, то он будет
совершать колебательные движения
бесконечно долго. Из рисунка 4 видно,
что величина силы
колебательные движения. Если на маятник
не действуют силы трения, то он будет
совершать колебательные движения
бесконечно долго. Из рисунка 4 видно,
что величина силы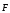 связана с величиной силы тяжести
связана с величиной силы тяжести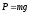 ,
соотношением:
,
соотношением:
F = mgSinφ (11)
Зависимость
возвращающей силы от смещения,
характеризуемого углом φ, в уравнении
(11), нелинейная, следовательно, и колебания
маятника будут не гармоническими.
Однако, в случае малых колебаний маятника,
когда угол отклонения φ столь мал
(до 5о), чтоSinφ
=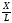 ≈
φ, возвращающая сила пропорциональна
углу φ и в этом случае (при малых
отклонениях) можно считать, что колебания
маятника происходят под действием
квазиупругой силы, и следовательно,
колебания являются гармоническими.
Малым углам отклоненияφсоответствует и малая величина смещенияХ. Подставив в уравнение (11) вместоSin, величину
≈
φ, возвращающая сила пропорциональна
углу φ и в этом случае (при малых
отклонениях) можно считать, что колебания
маятника происходят под действием
квазиупругой силы, и следовательно,
колебания являются гармоническими.
Малым углам отклоненияφсоответствует и малая величина смещенияХ. Подставив в уравнение (11) вместоSin, величину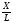 и, учитывая, что при малых углах отклоненияφ, вектор силы
и, учитывая, что при малых углах отклоненияφ, вектор силы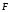 практически совпадет с отрезком смещения
Х, но направлен противоположно отклонению,
окончательно можно записать возвращающую
(квазиупругую) силу в виде
практически совпадет с отрезком смещения
Х, но направлен противоположно отклонению,
окончательно можно записать возвращающую
(квазиупругую) силу в виде
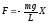 .
(12)
.
(12)
Следовательно, при малых углах отклонения φ, на маятник будет действовать квазиупругая сила и он будет совершать гармонические колебания. Найдем период таких гармонических колебаний математического маятника. Для этого запишем второй закон Ньютона в скалярном виде:
mα
=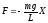 (13)
(13)
где α =
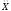 –ускорение колеблющегося шарика
математического маятника, Сократив в
уравнении (13) массу, получим уравнение
в виде:
–ускорение колеблющегося шарика
математического маятника, Сократив в
уравнении (13) массу, получим уравнение
в виде:
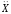 =
-
=
-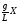 или
или
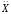 +
+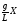 =
0.(14)
=
0.(14)
Так как в этих уравнениях величины g иLвсегда положительные, то их отношение можно приравнять к квадрату некоторой величины ω2:
ω2 =
 .(15)
.(15)
