Лаб1

ТЕМА: ИСПОЛЬЗОВАНИЕ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ ДЛЯ ОПРЕДЕЛЕНИЯ ГРАНИЦ ФИГУР НА ПЛОСКОСТИ

Краткие теоретические сведения: Метод координат на плоскости

Геометрические фигуры (окружности, прямые, параболы, ромбы, прямоугольники) на плоскости можно описать уравнениями в декартовой прямоугольной системе координат (x, y):

у = f(x), или x = f(y), или f(x, y) = 0.

Встречаются ситуации, когда по рисунку требуется восстановить уравнения фигур. Далее будут рассмотрены уравнения основных геометрических фигур.

1. Прямая: Общее уравнение прямой, не параллельной оси OY, имеет вид: y = ax + b.

Чтобы найти коэффициенты a и b, выберите две различные точки с целочисленными координатами (для простоты вычислений) и подставив в общее уравнение координаты указанных точек, получите систему из двух линейных уравнений с двумя неизвестными. Решив систему, восстановите уравнение прямой.

При этом надо учесть, что точки, лежащие ниже прямой y = ax + b., удовлетворяют неравенству y < a x + b, которое означает, что при каждом фиксированном значении x координата   y  любой точки (x, y), лежащей ниже прямой, меньше координаты y точки, лежащей на прямой, которая равна a x + b. Соответственно точки, лежащие выше прямой y = ax + b., удовлетворяют неравенству y > ax + b.

2. Окружность: координаты точек (x, y), лежащих на окружности радиуса R с центром в точке (a, b), удовлетворяют уравнению: (x — a) 2 + (y — b)2 = R 2 .

3. Ромб: Координаты точек, лежащих на ромбе, показанном на рис. 1, удовлетворяют уравнению |x| + |y | = 1.

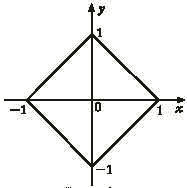
Рис.1 - Единичный ромб

Для проверки раскройте знак модуля и получите уравнения прямых для каждой из четвертей. Для точек первой четверти при x > 0, y > 0 имеем:   x + y   =1  — это уравнение прямой, проходящей через точки (1, 0) и (0, 1), что соответствует рисунку. Точки внутри ромба удовлетворяют неравенству |x| + |y| < 1.

При растяжении линии в k раз по оси x ее уравнение отличается от исходного тем, что х делится на k. Аналогично, если линия растягивается по y в k раз, то в ее уравнении y надо разделить на k. При сдвиге линии по оси x на величину c в ее уравнении вместо x надо взять x — c, при сдвиге по y на с надо в уравнении y заменить на y — c .

4. Парабола:

Вертикальная парабола Координаты точек  (x, y) , лежащих на параболе, проходящей через начало координат и точки (1, 1) и удовлетворяют уравнению y = x ²

Вертикальная парабола на рисунках 2-4 получается из рассмотренной выше растяжением по оси y в 2 раза и сдвигом по оси y на -1, поэтому ее уравнение получится из уравнения выше умножением y на 2 и заменой y на y -(-1).

Окончательно, уравнение имеет вид Y= 2X² -1

Координаты точек внутри (выше, над) параболы удовлетворяют неравенству Y>2X² -1.

Рис.2 - Внутри параболы Y= 2X2 -1	Рис.3 - Ниже параболы Y= 2X2 -1	Рис.4 - Левее параболы Y= 2X2 -1

Горизонтальная парабола: Уравнение x = y ²

Задание на лабораторную работу

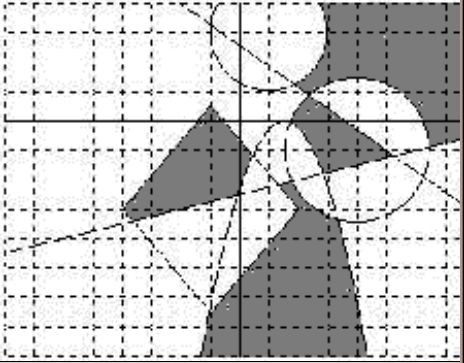
На рисунках на координатной плоскости изображены окружности, прямые, параболы, ромбы, прямоугольники (некоторые из линий могут отсутствовать); изображены также оси координат и координатная сетка, линии которой проведены через единицу масштаба. Несколько областей, ограниченных этими линиями, заштрихованы.

ВСТАВКА А

Рисунок 0	Рисунок 1
Рисунок 2	Рисунок 3
Рисунок 4	Рисунок 5

ВСТАВКА Б – Положение рисунка

0. Исходное

1. Поворот рисунка по часовой стрелке на 90

2. Поворот рисунка по часовой стрелке на 180

3. Поворот рисунка по часовой стрелке на 270

Требуется:

Составить программу, которая считывает координаты заданного (преподавателем) числа точек и определяет, принадлежит ли точка с координатами (x₀,y₀) фигуре, состоящей из всех заштрихованных на рисунке областей, или нет.

Индивидуальное задание для данной работы формируется на основе персонального номера студента, выданного преподавателем.

Порядок выполнения работы

1. В декартовой системе координат построить область в соответствии с индивидуальным заданием – по индивидуальному номеру определяется номер рисунка (Вставка А) и его положение (Вставка Б).

2. Восстановить по рисунку уравнения всех линий, изображенных на нем.

3. Составить блок-схема алгоритма.

4. Проводится кодирование и отладка программу.

5. Подготовить отчет.

Отчет должен содержать

1. Блок-схему алгоритма

2. График заданной области

3. Листинг программы на языке Паскаль

Пример программы

Program Lab1;

Uses crt;

Var

I:Integer;

N:Integer;

X,Y:Real;

Begin

ClrScr;

Write('Введите количество точек');

Readln(N);

For i:= 1 to N Do

Begin

Write('Введите X ');

Readln(X);

Write('Введите Y ');

Readln(Y);

{ Логические выражения, описывающие данную область}

End;

Readkey;

End.

Пример выполнения задания.

Приведем образец для выполнения задания на примере рис. 5.

Рис.5 – Пример 5 заштрихованной области

На данном рисунке изображено пять линий: две окружности, ромб и две параболы. Они ограничивают четыре заштрихованные части плоскости.

Восстановим уравнения этих линий.

Левая окружность имеет радиус 2,5. Центр ее в точке (—1, 2). Уравнение: (x + 1) ²+ (y — 2) ² = 2,5 ² .

Точки внутри левого круга удовлетворяют неравенству: (x+ 1) ² + (y — 2) ² < 2,5 ² .

Правая окружность имеет радиус 3. Центр ее — в точке (3, —1).

Поэтому, ее уравнение (x — 3) ² + (y + 1) ² = 3 ² . Аналогично, точки внутри правого круга удовлетворяют неравенству: (x — 3) ² +(y+1)² < 3 ².

Ромб на рис. 5 отличается от единичного , что он растянут в 4 раза по оси x и в 3 раза по оси y и его центр смещен в точку (—2, —2). Поэтому для него получаем уравнение |x + 2| / 4 + |y + 2| / 3 = 1. Для проверки можно подставить координаты вершин ромба в уравнение и убедиться, что они удовлетворяют ему. Координаты точек внутри ромба удовлетворяют неравенству |x + 2| / 4 + |y + 2| / 3 <

Уравнение прямой. 1 = a(—2) + b,

—2 = a*2 + b. Решив систему, получим a = —3/4, b = —1/2. Получаем уравнение прямой y = —3/4x — 1/2.

Уравнения параболы: Вертикальная парабола примера получается из рассмотренной выше сжатием по оси y в 2 раза и сдвигом по оси y на —5, поэтому ее уравнение получится из уравнения выше делением y на 1/2 и заменой y на y — (—5). В результате получаем уравнение (y + 5) / 0,5 = x 2 или y = 0,5x 2 — 5.

Аналогично горизонтальная парабола получается из параболы x = y 2 сдвигом на —1 по x и на —2 по y. Ее уравнение имеет вид: x — (—1) = (y — (—2)) 2 или x = (y + 2) 2 — 1. Координаты точек внутри (над) первой параболы удовлетворяют неравенствуy > 0,5x 2 — 5. Координаты точек внутри (правее) второй параболы удовлетворяют неравенству x > (y + 2) 2 — 1.

Рассмотрим теперь заштрихованные области.

Область 1 представляет собой точки, находящиеся в круге 1 И   НЕ  в круге  2, И  НЕ  внутри ромба.

Область 2 представляет собой точки, находящиеся в ромбе И внутри параболы 1, И   НЕ  в круге 1,  И  НЕ внутри параболы 2.

Область 3 представляет собой точки, находящиеся в параболе 1 И в параболе 2, И  НЕ  внутри ромба, И в круге 2.

Область 4 – внешняя. Описание таких открытых областей отличается от рассмотренных выше, нужно быть внимательным - на первый взгляд кажется, что область 4 представляет собой множество точек, находящихся НЕ внутри параболы 1 И НЕ внутри параболы 2 И НЕ в круге 2. Но этому же условию удовлетворяют, например, и точки слева от параболы 1,не входящие в рассматриваемую область. Поэтому для описания точек, принадлежащих 4-й области, надо добавить условие: И лежащие в первой четверти — то есть удовлетворяют системе неравенств: И лежащие в первой четверти — то есть удовлетворяют системе неравенств: x > 0 И y > 0.

ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА

1. Андреева Е.В., Гущин И.С. Логические выражения. Практикум по информатике. // Информатика. Приложение к газете "Первое сентября". - 2001. - N 36. - С. 5-9

ПРИЛОЖЕНИЕ

Рисунок 1

Рисунок 2

Рисунок 6

Рисунок 5