
Индуктивность катушки
Способность катушки индуктировать на себе э. д. с. самоиндукции называется индуктивностью катушки.
Единицей измерения индуктивности является Генри (Гн)
Индуктивностью в 1 Гн обладает такая катушка, изменения тока в которой на 1 А в секунду создает э. д. с. самоиндукции равной 1 В.
10-3 Гн миллигенри мГн
10-6 Гн микрогенри мкГн
Величина индуктивности прямо пропорциональна размерам катушки и числу витков. Кроме того, индуктивность зависит также от материала введенного в катушку сердечника и наличия экрана. Качество работы катушки индуктивности в цепях переменного тока характеризуется добротностью. Добротность Q катушки определяют как отношение ее индуктивного сопротивления ХL= ωL=2пfL к активному R, при рабочей частоте f:Q=ωL/R=2пfL/R. Активное сопротивление включает сопротивление провода обмотки катушки и сопротивление, обусловленное потерями электрической энергии в каркасе, сердечнике, экране и изоляции. Чем меньше активное сопротивление, тем выше добротность катушки и ее качество. Витки катушки, разделенные слоем изоляции, образуют элементарный конденсатор. В многослойных катушках емкость возникает между отделными слоями. Таким образом, катушка обладает не только индуктивными, но и емкостными свойствами. В большинстве случаев собственная емкость катушки является вредной, и ее стремятся уменьшить. Для этого применяются специальные формы каркаса катушки и способы намотки провода.
Назначение сердечников в катушках индуктивности
Сердечник увеличивает индуктивность катушки. Действительно катушка с сердечником обладает большим магнитным полем а значит на ней будет индуктироваться большая э. д. с. самоиндукции.
Если положение сердечника в катушке можно изменять, значит можно изменять индуктивность катушки.
Изображение сердечников на схемах


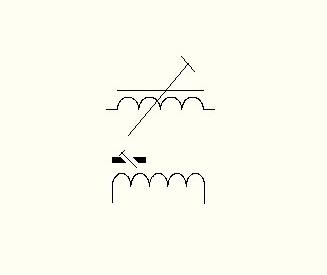
Взаимоиндукция
Явление взаимоиндукции наблюдается между близко расположенными катушками. Сущность взаимоиндукции заключается в переносе электрической энергии из одной цепи в другую посредством общего магнитного поля: в одном из контуров электрическая энергия преобразуется в энергию магнитного поля, в другом контуре происходит обратный переход энергии магнитного поля в электрическую энергию. Из сказанного следует, что магнитное поле является переносчиком электрической энергии из одной цепи в другую.
Взаимная индуктивность между двумя катушками зависит от их размеров, числа витков, взаимного расположения и магнитной проницаемости среды.
N18
Электромагнитные колебания — это периодические изменения со временем электрических и магнитных величин (заряда, силы тока, напряжения, напряженности, магнитной индукции и др.) в электрической цепи.
Для возбуждения и поддержания электромагнитных колебаний требуются определенные системы, простейшей из которых является колебательный контур — цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R (это может быть сопротивление провода катушки и проводов, соединяющих катушку с конденсатором) (рис. 1). Идеальный контур Томсона — колебательный контур без активного сопротивления (R = 0).

Рис. 1
Рассмотрим свободные электромагнитные колебания — колебания, происходящие в идеальном колебательном контуре за счет расходования сообщенной этому контуру энергии, которая в дальнейшем не пополняется. Рисунок 2 иллюстрирует характерные стадии колебаний в контуре за один период.
Отсчет времени t мы начинаем с момента подключения к контуру заряженного конденсатора. В этот момент (рис. 2, а) напряженность электрического поля E⃗ в конденсаторе (направленная сверху вниз), а также напряжение U на обкладках конденсатора максимальны, а тока в контуре еще нет, следовательно, отсутствует и магнитное поле.
При этом вся энергия W колебательного контура заключена в электрическом поле конденсатора, т.е.
W=We0=CU202=q202C.
В промежутке времени от 0 до T4 (рис. 2, б) конденсатор, разряжаясь, создает через контур ток I, идущий по часовой стрелке. При этом согласно правилу Ленца в катушке возникает ЭДС самоиндукции, препятствующая нарастанию этого тока. При разряде конденсатора уменьшаются напряженность электрического поля E⃗ (сохраняя прежнее направление) и напряжение U между его обкладками, следовательно, уменьшается энергия электрического поля в конденсаторе. Сила тока I и индукция B⃗ магнитного поля, создаваемого этим током, увеличиваются, т.е. возрастает энергия магнитного поля в катушке индуктивности. Следовательно, энергия электростатического поля конденсатора превращается в энергию магнитного поля катушки.
К моменту времени t=T4 (рис. 2, в) конденсатор полностью разряжается, напряжение U между его обкладками становится равным нулю, и электрическое поле в нем отсутствует E⃗ =0. К этому времени ток 1 в контуре и индукция B⃗ магнитного поля этого тока достигают максимальных значений. Следовательно, вся энергия контура заключена в этот момент в его магнитном поле, т.е.
W=WM0=LI202.
При этом вся энергия W колебательного контура заключена в электрическом поле конденсатора, т.е.
W=We0=CU202=q202C.
В промежутке времени от 0 до T4 (рис. 2, б) конденсатор, разряжаясь, создает через контур ток I, идущий по часовой стрелке. При этом согласно правилу Ленца в катушке возникает ЭДС самоиндукции, препятствующая нарастанию этого тока. При разряде конденсатора уменьшаются напряженность электрического поля E⃗ (сохраняя прежнее направление) и напряжение U между его обкладками, следовательно, уменьшается энергия электрического поля в конденсаторе. Сила тока I и индукция B⃗ магнитного поля, создаваемого этим током, увеличиваются, т.е. возрастает энергия магнитного поля в катушке индуктивности. Следовательно, энергия электростатического поля конденсатора превращается в энергию магнитного поля катушки.
К моменту времени t=T4 (рис. 2, в) конденсатор полностью разряжается, напряжение U между его обкладками становится равным нулю, и электрическое поле в нем отсутствует E⃗ =0. К этому времени ток 1 в контуре и индукция B⃗ магнитного поля этого тока достигают максимальных значений. Следовательно, вся энергия контура заключена в этот момент в его магнитном поле, т.е.
W=WM0=LI202.
