2.3.Построение графиков чётной и нечётной функций

Как уже отмечалось, для чётной функции y=f(x) во всей области изменения её аргумента справедливо соотношение f(x)=f(- x). Следовательно, функция такого рода принимает одинаковые значения при всех значениях аргумента, равных по абсолютной величине, но противоположных по знаку. График чётной функции симметричен относительно оси ординат.

Для построения графика чётной функции y=f(x) следует построить ветвь графика этой функции только в области положительных значений аргумента x. График функции y=f(x) в области отрицательных значений аргумента симметричен построенной ветви относительно оси ординат и получается отражением её относительно этой оси.

Пример 8. Построить график функции y=.

Р е ш е н и е: Данная функция – чётная, поэтому достаточно построить её график лишь в области положительных значений x (точка x=0 не входит в область определения функции). При x>0 исходная функция имеет вид y=. График функцииy=в области отрицательных значенийx получаем отражением относительно оси ординат (рис.11).

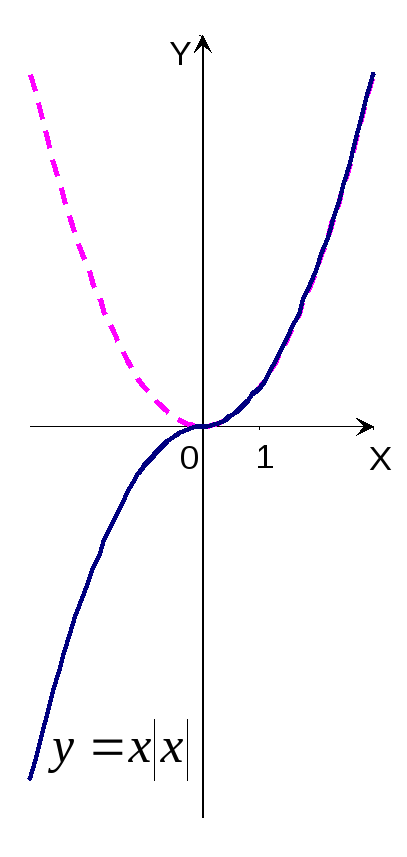
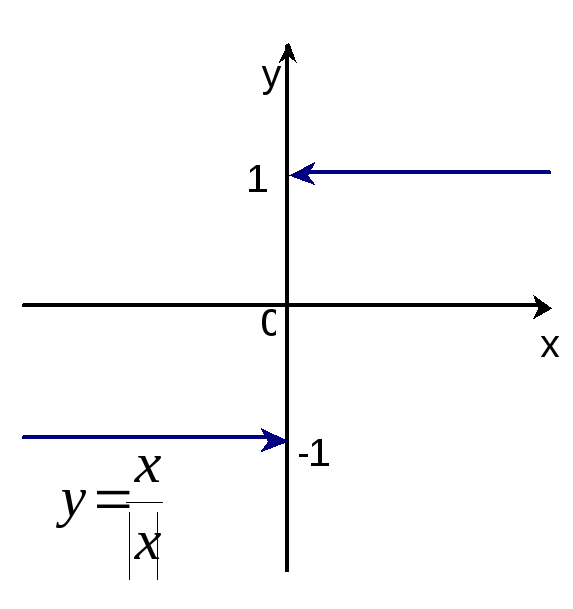
Рис.11

Рис.12

Рис.13.

Для нечётной функции y=f(x) в области всех значений аргумента справедливо равенство f(-x)= -f(x). Таким образом, в области отрицательных значений аргумента ординаты графика нечётной функции равны по величине, но противоположны по знаку ординатам графика той же функции при соответствующих положительных значениях x. График нечётной функции симметричен относительно начала координат.

Для построения графика нечётной функции y=f(x) следует строить ветвь графика этой функции только в области положительных значений аргумента (x).

График функции y=f(x) в области отрицательных значений аргумента симметричен построенной ветви относительно начала координат и может быть получен отражением этой ветви относительно оси ординат с последующим отражением в области отрицательных значений x относительно оси абсцисс.

Пример 9. Построить график функции y=x.

Р е ш е н и е: Исходная функция является нечётной, поэтому строим её в области положительных значений аргумента (x), где она имеет вид y=x². График функции y=x в области отрицательных значений аргумента получаем отражением построенной ветви относительно начала координат (рис.12).

Пример 10. Построить график функции y= .

Р е ш е н и е: Данная функция является нечётной, поэтому строим её график лишь в области x>0 (точка x=0 не входит в область определения функции), где она имеет вид y=1. Ветвь графика данной функции при x<0 получаем отражением относительно начала координат построенной ветви кривой (рис.13). Стрелки означают, что точки (0,1) и (0,-1) не принадлежат графику.

2.4. Построение графика обратной функции

Прямая и обратная функции выражают одну и ту же зависимость между переменными x и y, с тем только отличием, что в обратной функции эти переменные поменялись ролями, что равносильно изменению обозначений осей координат. Поэтому график обратной функции симметричен графику прямой функции относительно биссектрисы I и III координатных углов, т.е. относительно прямой y=x. Таким образом, получаем следующее правило.

Для построения графика функции y=, обратной по отношению к функцииy=f(x), следует построить график y=f(x) и отразить его относительно прямой y=x.

Пример 11. Построить график функции y=.

Р е ш е н и е: Ч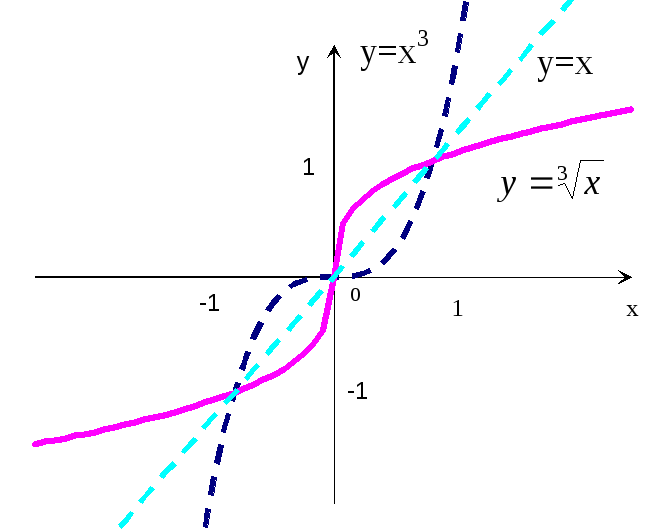тобы построить график данной функции, рассмотрим график параболыy=x² (рис.14 – пунктирная кривая) и график обратной к ней функции y=, получаемый отражением параболы относительно прямой y=x. Обратная функция является двузначной. В силу того, что исходная функция y=однозначна и область её изменения есть полуинтервал 0y<, графиком функцииy=является верхняя ветвь отражённой параболы (сплошная кривая). Нижняя же ветвь (штрих-пунктир) представляет собой график функцииy= -.

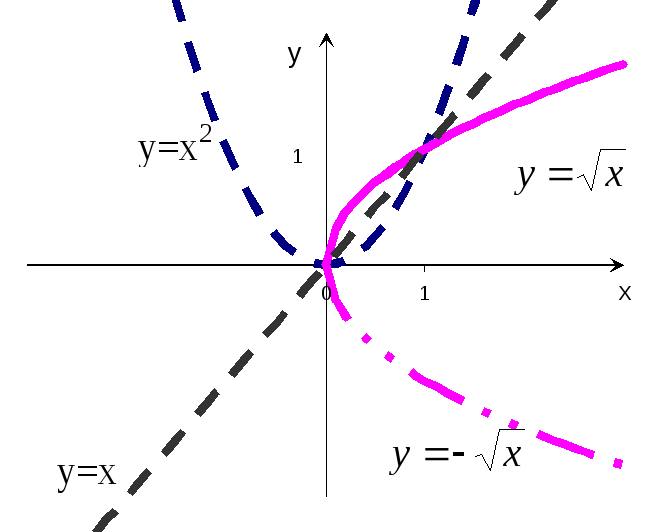
Рис.15

Пример 12. Построить график функции y= .

Р е ш е н и е: Данная функция является обратной по отношению к функции y=x, поэтому строим график функции y=x и отражаем его относительно прямой y=x (рис.15).