1.2 Перенос вдоль оси абсцисс

Пусть тебуется построить график функции y=f(x+a). Рассмотрим функцию y=f(x), которая в некоторой точке x=x₁ принимает значение y₁=f(x₁). Очевидно, функция y=f(x+a) примет такое же значение в точке x₂, координата которой определяется из равенства x₂+a=x₁, т.е. x₂=x₁-a, причём рассматриваемое равенство справедливо для совокупности всех значений x из области определения функции. Следовательно, график функции y=f(x+a) может быть получен параллельным перемещением графика функции y=f(x) вдоль оси абсцисс влево на a единиц при a>0 или вправо на a единиц при a<0. Параллельное же перемещение графика вдоль оси абсцисс на a единиц эквивалентно переносу оси ординат на столько же единиц, но в противоположную сторону. Таким образом, получаем следующее правило.

Для построения графика функции y=f(x+a) следует построить график функции y=f(x) и перенести ось ординат на a единиц вправо при a>0 или на a единиц влево при a<0 .Полученный в новой системе координат график является графиком функции y=f(x+a).

Пример 3. Построить график функции y=log₂(x+2).

Р е ш е н и е:

Строим график функции y=log₂x. Переносим ось ординат на 2 единицы вправо, и в полученной таким образом новой системе координат имеем график функции y=log₂(x+2).

Прямая x=-2 (первоначальная ось y) является вертикальной асимптотой. График пересекает ось абсцисс в точке x= -1, а ось ординат - в точке y=1 (рис.6).

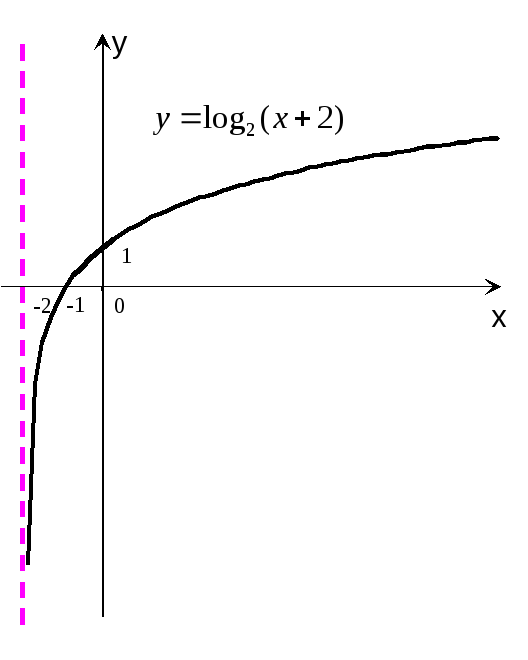
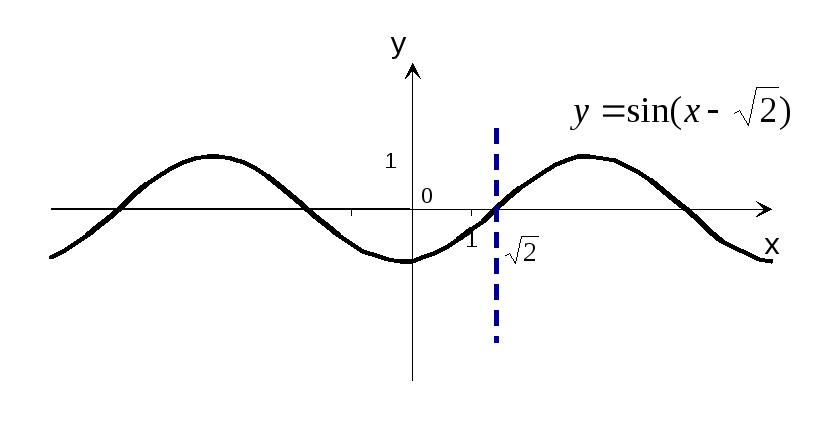
Рис.6 Рис.7

Пример 4. Построить график функции y=sin(x-).

Р е ш е н и е:

Строим график функции y=sin x. Переносим ось ординат на единиц влево и во вновь полученной системе координат имеем график функцииy=sin(x-) (рис 7). Координаты точек пересечения графика с осью абсцисс находим из условияsin(x-)=0, откудаx=+k, где k=0, 1, 2, … .

2.Отражение

2.1.Построение графика функции вида y=f(-x)

Очевидно, что функции y=f(-x) и y=f(x) принимают равные значения в точках, абсциссы которых равны по абсолютной величине, но противоположны по знаку. Иначе говоря, ординаты графика функции y=f(-x) в области положительных (отрицательных) значений x будут равны ординатам графика функции y=f(x) при соответствующих по абсолютной величине отрицательных (положительных) значениях x. Таким образом, получаем следующее правило.

Для построения графика функции y=f(-x) следует построить график функции y=f(x) и отразить его относительно оси ординат. Полученный график является графиком функции y=f(-x).

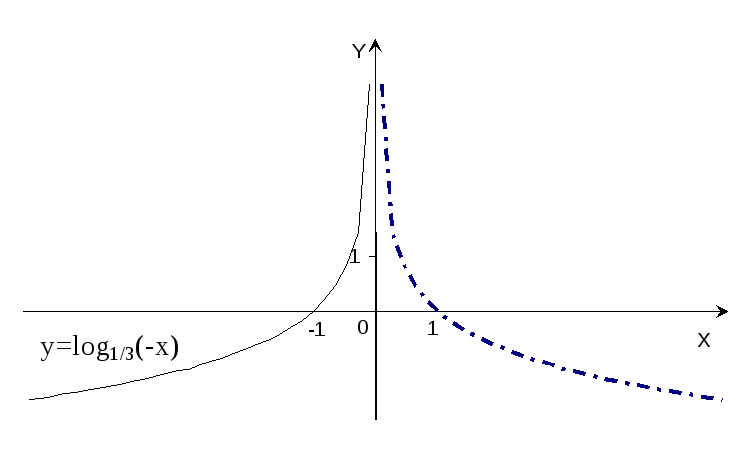
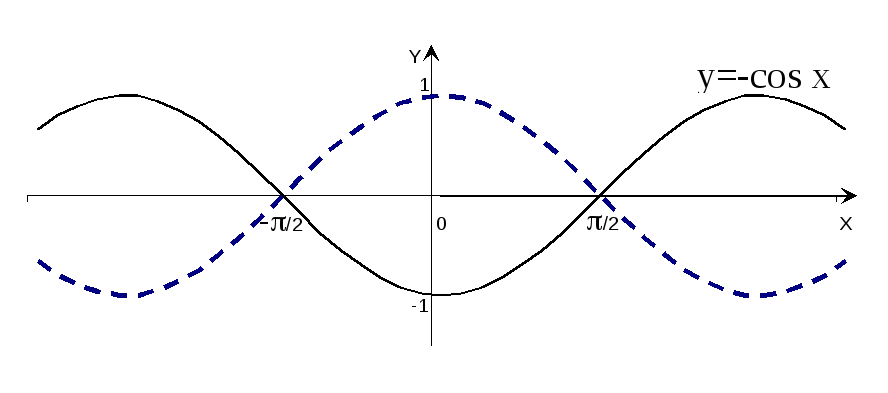
Рис.8 Рис.9

Пример 5. Построить график функции y=(-x).

Р е ш е н и е : Строим график функции y=x и отражением его относительно оси ординат получаем график функции y=(-x) (рис.8).

2.2.Построение графика функции вида y= -f(x).

Ординаты графика функции y= -f(x) при всех значениях аргумента равны по абсолютной величине, но противоположны по знаку ординатам графика функции y= f(x) при тех же значениях аргумента. Таким образом, получаем следующее правило.

Для построения графика функции y= -f(x) следует построить график функции

y=f(x) и отразить его относительно оси абсцисс.

Пример 6. Построить график функции y= - cos x.

Р е ш е н и е: С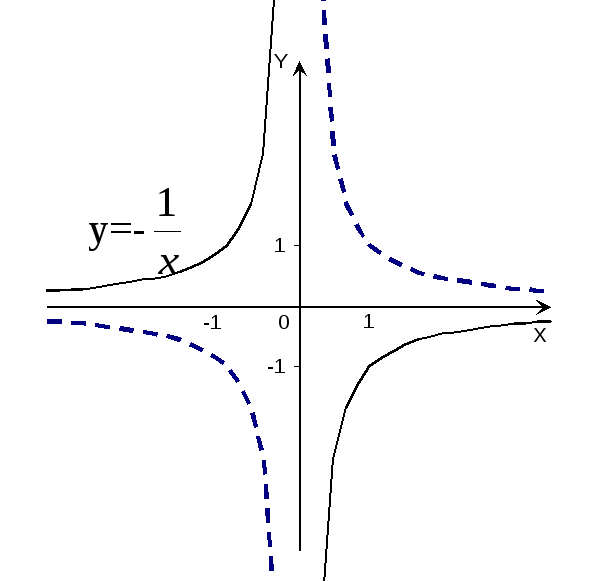троим график функцииy= cos x (рис. 9 – пунктирная кривая) и, отражая его относительно оси абсцисс, получаем график функции y= - cos x.

Пример 7. Построить график функции y= - .

Р е ш е н и е: Строим график функции y= и, отражая его относительно оси абсцисс, получаем график функцииy= - (рис.10).

Рис.10