
- •Элементарная математика
- •Часть1. (Алгебра и начала анализа)
- •Основные определения
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график. Взаимное расположение графика квадратичной функции и оси абсцисс.
- •Свойства:
- •Взаимное расположение графика квадратичной функции и оси абсцисс.
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства степени. Показательная функция и её свойства.
- •Свойства степени с натуральным показателем
- •Свойства степени с действительным показателем
- •Свойства:
- •Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, степени, частного. Зависимость между логарифмами числа по разным основаниям.
- •Свойства:
- •Преобразование графиков функций
- •Формула корней квадратного уравнения. Теорема Виета. Формула корней квадратного уравнения.
- •Теорема Виета.
- •Разложение квадратного трехчлена на линейные множители
- •Формулы сокращенного умножения.
- •Свойства числовых неравенств.
- •Свойства числовых равенств.
- •Метод интервалов
- •Формулы приведения.
- •Зависимости между тригонометрическими функциями одного и того же аргумента
- •Тригонометрические функции двойного и половинного аргумента
- •Преобразование суммы (разности) в произведение
- •Преобразование произведения в сумму.
- •Обратные тригонометрические функции. (Теорема о корне и теорема об обратной функции)
- •Арксинус
- •Арккосинус
- •Арктангенс
- •Арккотангенс
- •Решение уравнений вида
- •Решение уравнений вида
- •Решение уравнений вида
- •Решение уравнений вида
- •Решение уравнений типа с помощью вспомогательного аргумента.
- •Признаки делимости на 2,3,5,9,10.
- •Делимость на 2
- •Делимость на 3 на 9
- •Делимость на 5
- •Делимость на 10
- •Квадратный корень из числа. Арифметический квадратный корень, его свойства. Корень и арифметический корень п-ой степени
- •Свойства арифметического квадратного корня
- •Cвойства
- •Геометрическая прогрессия. Формулы п-го члена и суммы п первых членов геометрической прогрессии. Характеристическое свойство геометрической прогрессии.
- •Тригонометрическая окружность
- •Сборник формул
- •Библиографический список
Свойства:
Область определения функции:
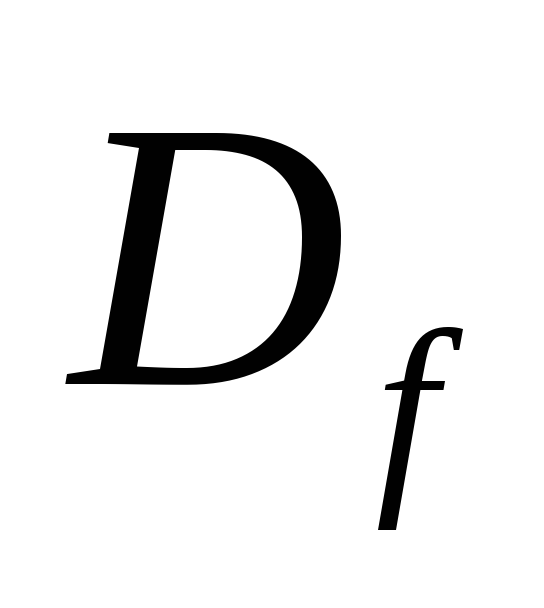
![]() ,
по определению логарифма числа.
,
по определению логарифма числа.
Множество значений функции:
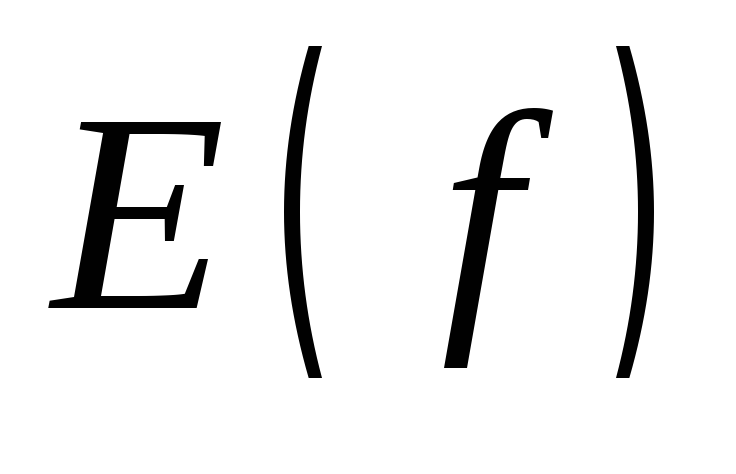
![]()
Периодичность:
Функция
![]() не является периодической (почему?).
не является периодической (почему?).
Чётность/нечётность
Поскольку
![]() ,
то есть область определения функции
не симметрична относительно нуля, то
есть если
,
то есть область определения функции
не симметрична относительно нуля, то
есть если![]() ,
то
,
то![]() ,
значит, функция
,
значит, функция
![]() является функцией общего вида.
является функцией общего вида.
Точки пересечения графика с осями координат.
Точки
пересечения с осью
![]() :
так как
:
так как![]()
![]() ,
то график функции не пересекает ось
,
то график функции не пересекает ось![]()
Точки
пересечения с осью
![]() , то есть
, то есть![]()
Промежутки знакопостоянства функции:
если
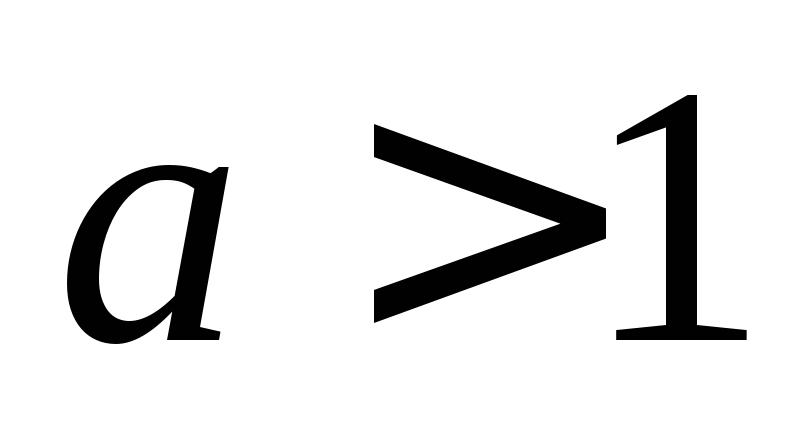 ,
то
,
то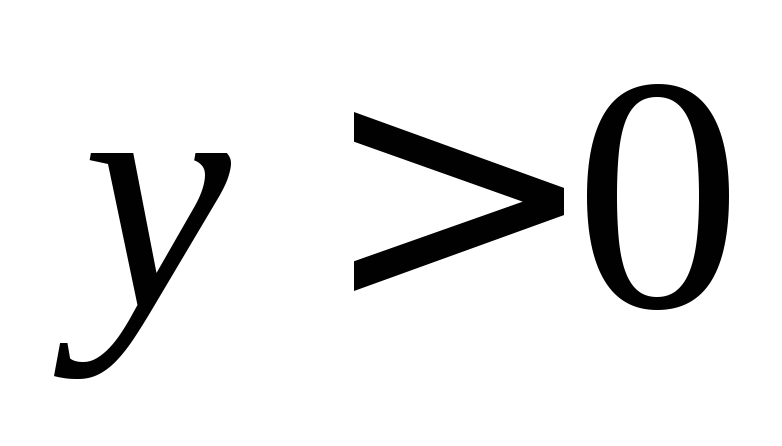 при
при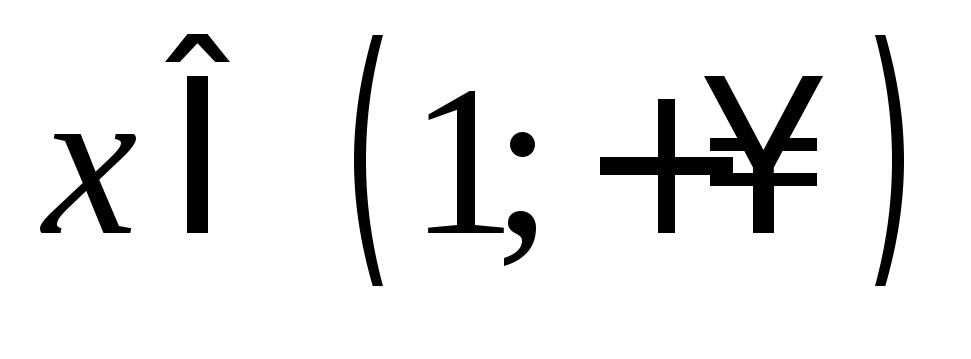 и
и при
при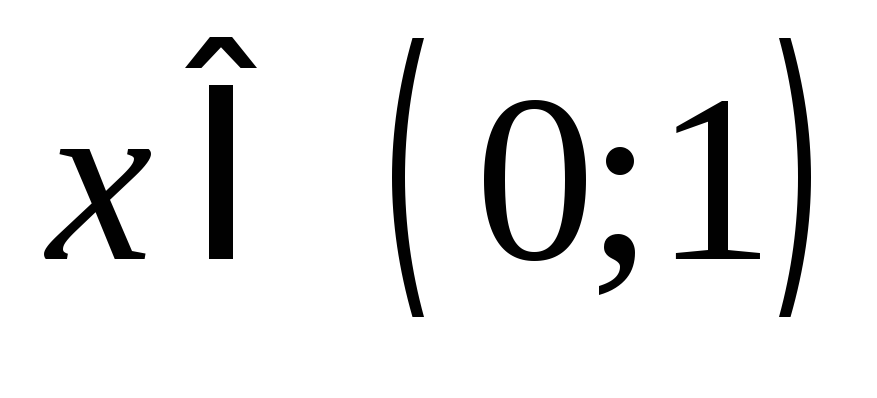
если
 ,
то
,
то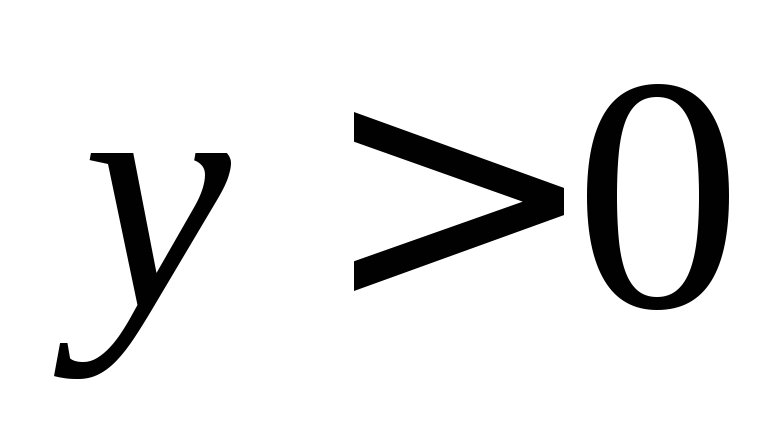 при
при и
и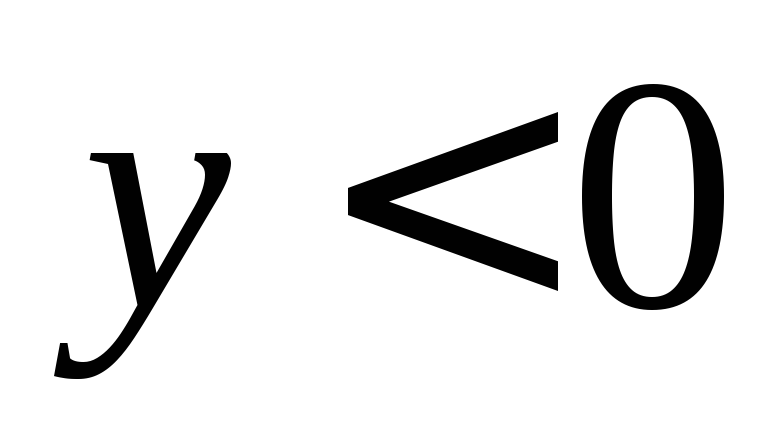 при
при
Интервалы возрастания/убывания
Если
![]() ,
то функция возрастает на всей области
определения
,
то функция возрастает на всей области
определения
Если
![]() ,
то функция убывает на всей области
определения
,
то функция убывает на всей области
определения
Доказательство:
Рассмотрим случай
 .
.
Пусть
![]() - произвольные действительные числа,
причем пусть для определенности
- произвольные действительные числа,
причем пусть для определенности![]() .
Докажем, что
.
Докажем, что
![]() .
.
Предположим
от противного, что
![]() ,
так как показательная функция
,
так как показательная функция![]() при
при![]() возрастает, то из неравенства
возрастает, то из неравенства![]() следует, что
следует, что![]() ,
но
,
но![]() ,
а
,
а![]() ,
то есть получили, что
,
то есть получили, что![]() ,
что противоречит условию, так как по
условию
,
что противоречит условию, так как по
условию![]() .
.
Теперь рассмотрим случай
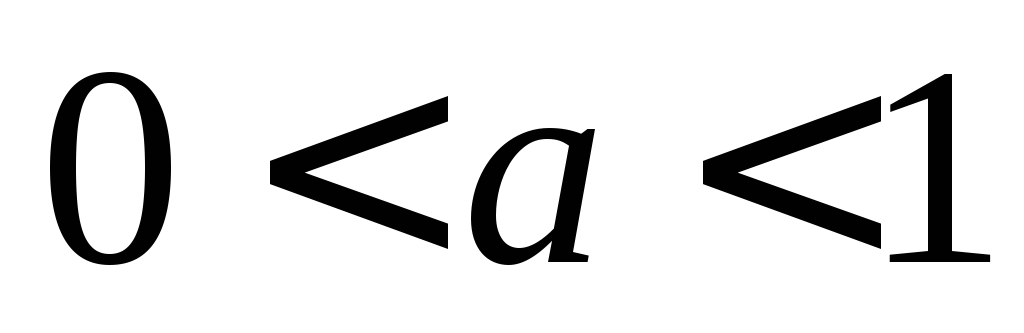 .
.
Пусть
![]() - произвольные действительные числа,
причем пусть для определенности
- произвольные действительные числа,
причем пусть для определенности![]() .
Докажем, что
.
Докажем, что![]() .
.
Предположим
от противного, что
![]() ,
так как показательная функция
,
так как показательная функция![]() при
при![]() убывает, то из неравенства
убывает, то из неравенства![]() следует, что,
следует, что,![]() ,
но
,
но![]() ,
а
,
а![]() ,
то есть получили, что
,
то есть получили, что![]() ,
что противоречит условию, так как по
условию
,
что противоречит условию, так как по
условию![]() .
.

Наибольшее/наименьшее значение функции
Функция
![]() не имеет наименьшего и наибольшего
значения, т.к. её множеством значений
является всё множество
не имеет наименьшего и наибольшего
значения, т.к. её множеством значений
является всё множество![]() .
.
График функции. (рис 12).
Преобразование графиков функций
|
«Новая функция» |
С |
Иллюстрация преобразования |
|
|
Параллельный
перенос графика функции
|
|
|
|
Параллельный
перенос графика функции
|
|
|
|
Симметрия относительно оси абсцисс |
|
|
|
Симметрия относительно оси ординат |
|
|
|
Если
Если
|
|
|
|
Если
Если
|
|
|
|
Т А
ту часть графика, которая расположена
ниже оси
|
|
|
|
Т Ту
часть графика, которая расположена
левее оси
|
|

 пособ
преобразования графика функции
пособ
преобразования графика функции право,
если
право,
если
 у
часть графика, которая расположена
выше оси
у
часть графика, которая расположена
выше оси у
часть графика, которая расположена
правее оси
у
часть графика, которая расположена
правее оси