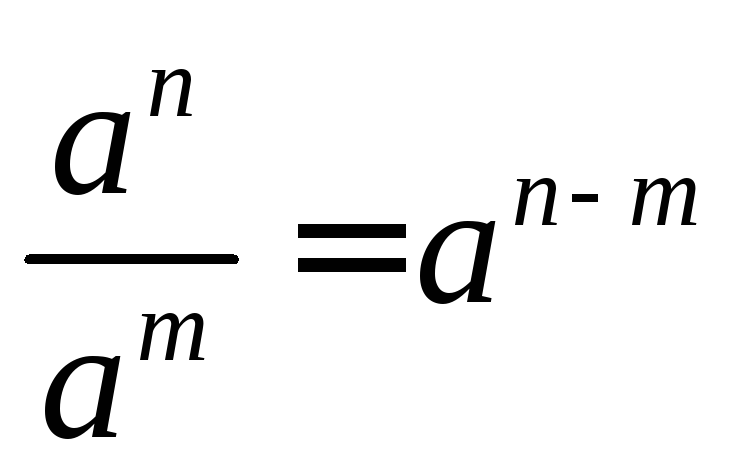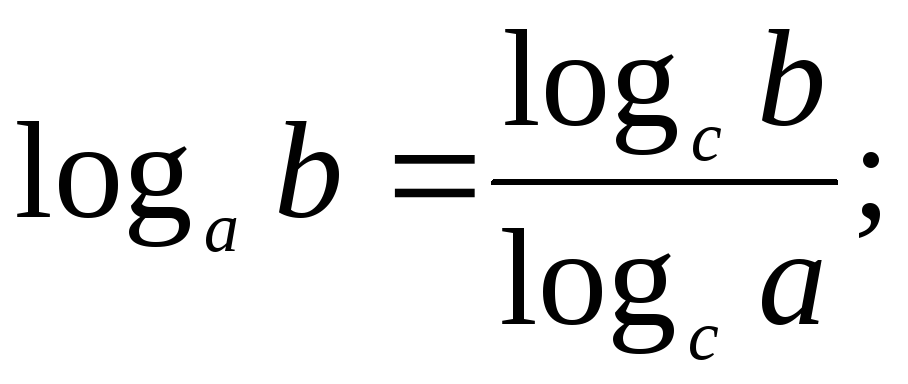- •Элементарная математика
- •Часть1. (Алгебра и начала анализа)
- •Основные определения
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график. Взаимное расположение графика квадратичной функции и оси абсцисс.
- •Свойства:
- •Взаимное расположение графика квадратичной функции и оси абсцисс.
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства функции и её график
- •Свойства:
- •Свойства степени. Показательная функция и её свойства.
- •Свойства степени с натуральным показателем
- •Свойства степени с действительным показателем
- •Свойства:
- •Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, степени, частного. Зависимость между логарифмами числа по разным основаниям.
- •Свойства:
- •Преобразование графиков функций
- •Формула корней квадратного уравнения. Теорема Виета. Формула корней квадратного уравнения.
- •Теорема Виета.
- •Разложение квадратного трехчлена на линейные множители
- •Формулы сокращенного умножения.
- •Свойства числовых неравенств.
- •Свойства числовых равенств.
- •Метод интервалов
- •Формулы приведения.
- •Зависимости между тригонометрическими функциями одного и того же аргумента
- •Тригонометрические функции двойного и половинного аргумента
- •Преобразование суммы (разности) в произведение
- •Преобразование произведения в сумму.
- •Обратные тригонометрические функции. (Теорема о корне и теорема об обратной функции)
- •Арксинус
- •Арккосинус
- •Арктангенс
- •Арккотангенс
- •Решение уравнений вида
- •Решение уравнений вида
- •Решение уравнений вида
- •Решение уравнений вида
- •Решение уравнений типа с помощью вспомогательного аргумента.
- •Признаки делимости на 2,3,5,9,10.
- •Делимость на 2
- •Делимость на 3 на 9
- •Делимость на 5
- •Делимость на 10
- •Квадратный корень из числа. Арифметический квадратный корень, его свойства. Корень и арифметический корень п-ой степени
- •Свойства арифметического квадратного корня
- •Cвойства
- •Геометрическая прогрессия. Формулы п-го члена и суммы п первых членов геометрической прогрессии. Характеристическое свойство геометрической прогрессии.
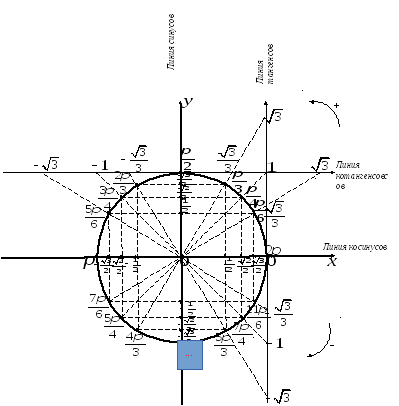
- •Тригонометрическая окружность
- •Сборник формул
- •Библиографический список
Геометрическая прогрессия. Формулы п-го члена и суммы п первых членов геометрической прогрессии. Характеристическое свойство геометрической прогрессии.
О.Геометрической прогрессией называется последовательность, в которой первый член отличен от нуля, а каждый из последующих равен предыдущему, умноженному на некоторое постоянное для данной последовательности число, отличное от нуля.
О.Это число называетсязнаменателем геометрической прогрессии q геометрической прогрессии.
Геометрическая
прогрессия задаётся своим первым членом
и знаменателем. Из определения
геометрической прогрессии следует,
что отношение любого её члена, начиная
со второго, к предыдущему члену равно
q, т.е. при любом
натуральномnверно
равенство![]() .
.
Формула n-го члена геометрической прогрессии.
Любой член
геометрической прогрессии можно
вычислить по формуле
![]() ,где
,где![]() -
член прогрессии с номеромn,
-
член прогрессии с номеромn,![]() -
первый член иq– её
знаменатель.
-
первый член иq– её
знаменатель.
Возьмём произвольное
натуральное n.Из
определения геометрической прогрессии
следует![]() .
.
Эта цепочка состоит из nравенств, поэтому для любого конечногоnона может быть выписана. Следовательно, любой член геометрической прогрессии можно вычислить, зная его номер, первый член прогрессии и её знаменатель.
Характеристическое свойство геометрической прогрессии с положительными членами.
Если последовательность положительных чисел является геометрической прогрессией, то все её члены, начиная со второго, являются средним геометрическим предшествующего и последующего членов.
Доказательство.
Из определения
геометрической прогрессии следует,
что
![]() .
.
Выразив из этого
равенства
![]() ,
получим
,
получим![]() .
.
Так как все члены
прогрессии положительны, то последнее
равенство равносильно следующему
![]() .
.
Теорема. (формула суммы n первых членов геометрической прогрессии).
Сумма n
первых членов геометрической
прогрессии равна
![]() ,при
,при![]() .
.
Доказательство.
Сумма nпервых членов геометрической прогрессии равна
![]() .
.
![]()
Домножим обе части
этого равенства на знаменатель
геометрической прогрессии
![]() .
.
Следовательно,
![]() .
Вычтем полученное равенство из
.
Вычтем полученное равенство из![]() .
Получим:
.
Получим:![]()
![]() .
.
Отсюда следует,
что
![]() .
При
.
При![]() это равенство равносильно доказываемому.
Теорема доказана.
это равенство равносильно доказываемому.
Теорема доказана.
Следствие.
![]() ,при
,при![]() .
.
Доказательство.
Выразим
![]() по формулеn-го члена
геометрической прогрессии и подставим
в формулу (1).
по формулеn-го члена
геометрической прогрессии и подставим
в формулу (1).
Геометрическая
прогрессия называется бесконечно
убывающей, если её знаменательq по абсолютной величине меньше
единицы![]() .
.
О.Суммой бесконечно убывающей геометрической прогрессииназывается число, к которому неограниченно приближается суммаnпервых членов бесконечно убывающей геометрической прогрессии при неограниченном увеличенииn.
Сумма
бесконечно убывающей геометрической
прогрессии равна
![]() .
.
Приложение
Тригонометрическая окружность
Сборник формул
|
ТРИГОНОМЕТРИЯ Основные тригонометрические тождества
Знаки тригонометрических функций по четвертям
Тригонометрические функции отрицательного аргумента
Выражение одной функции через другую Обратные функции
аргумента
Р
Функция алгебраической суммы двух аргументов
П
Функции половинного аргумента
|
АЛГЕБРА
Корни квадратных уравнений
Разложение квадратного трехчлена на множители
Логарифмы
Извлечение квадратного корня из квадрата. Определение модуля числа.
|










 ешение
простейших тригонометрических
уравнений
ешение
простейших тригонометрических
уравнений

 реобразование
Преобразование
реобразование
Преобразование ункции
двойного аргумента
ункции
двойного аргумента
 ункции
тройного аргумента
ункции
тройного аргумента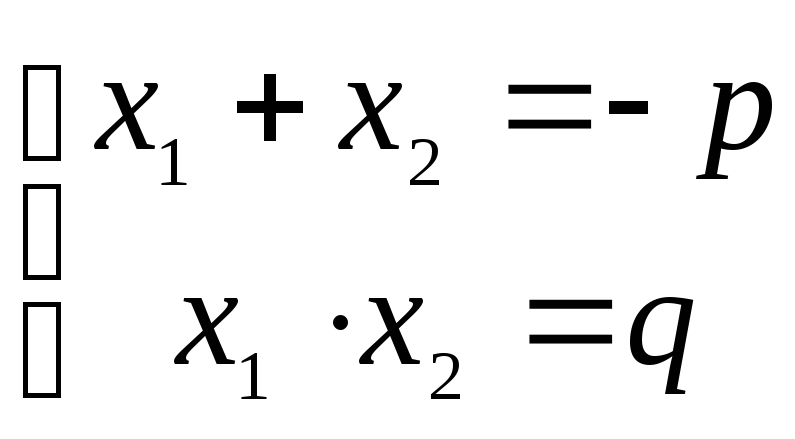
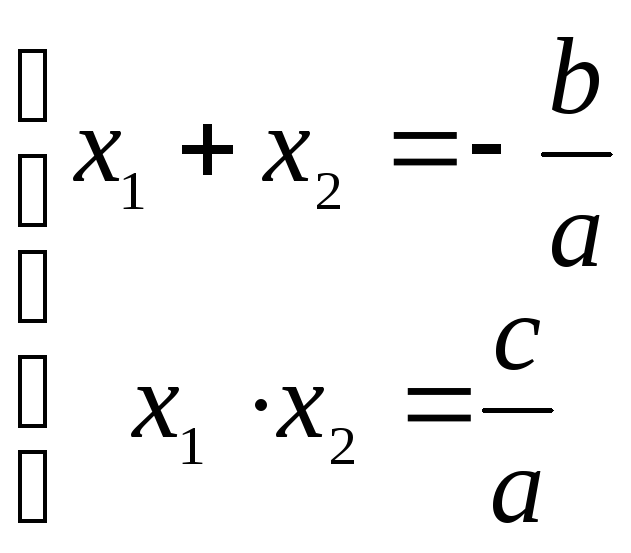

 тепени
и корни
тепени
и корни