Cвойства

1.

Доказательство:

- это такое неотрицательное число, степень которого равна.

Число неотрицательно. Поэтому достаточно проверить справедливость равенства

, которое вытекает из свойств степени с натуральным показателем и определения корня - ой степени:

.

2.

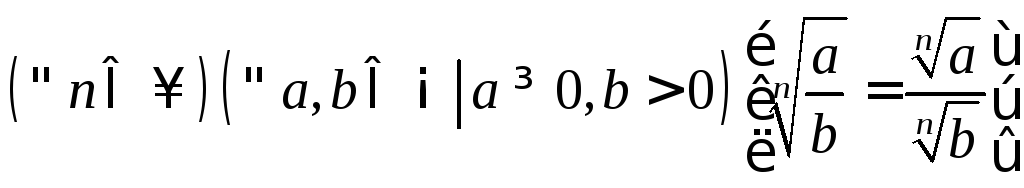
Доказательство:

- это такое неотрицательное число, степень которого равна.

Число неотрицательно. Поэтому достаточно проверить справедливость равенства

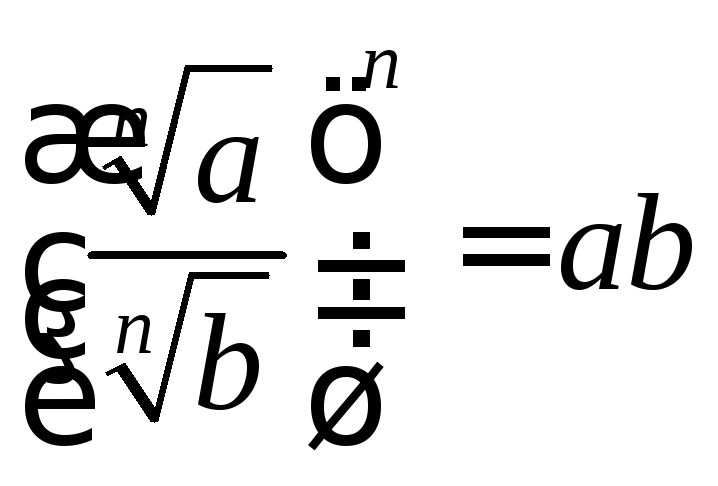, которое вытекает из свойств степени с натуральным показателем и определения корня - ой степени:

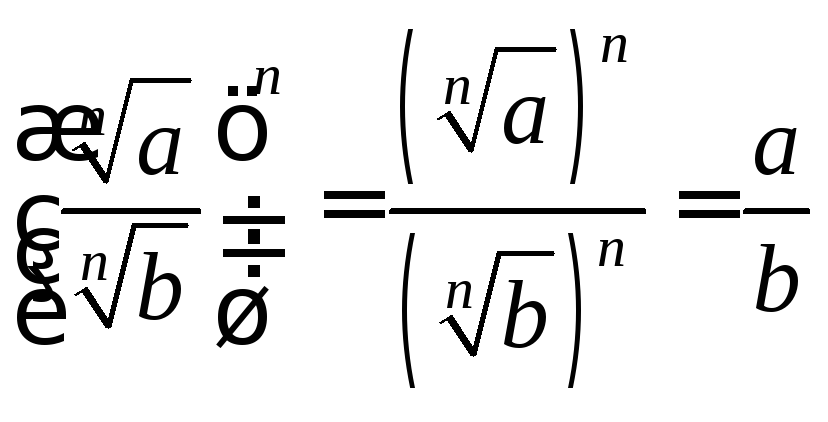
3.

Доказательство:

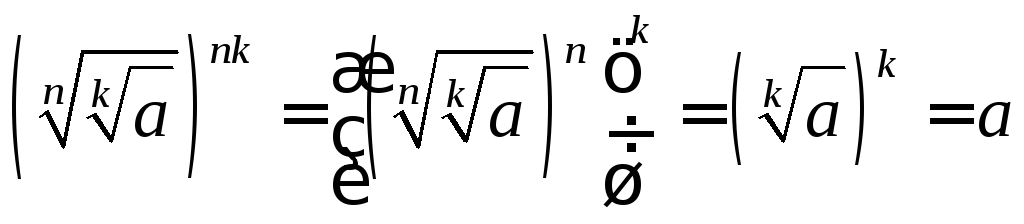
и

и

4.

(Доказать самостоятельно)

5.

Доказательство:

Заметим, что . Тогда.

Так как , то по определению арифметического квадратного корня

.

6.

Доказательство:

Будем доказывать методом от противного:

Пусть и.

Тогда , но по условию. Получили противоречие с условием. Значит наше предположение о том, чтоне верно. А верно то, что нужно доказать:.

35. Арифметическая прогрессия. Формулы п-го члена и суммы п первых членов арифметической прогрессии. Характеристическое свойство арифметической прогрессии.

О.Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом, постоянным для этой последовательности.

О.Это число называетсяразностью арифметической прогрессии прогрессии.

Арифметическая прогрессия задаётся своим первым членом и разностью. Из определения следует, что разность между любым членом арифметической прогрессии, начиная со второго, и предыдущим членом равна d, т.е. при любом натуральном n верно равенство .

Формула n-го члена арифметической прогрессии.

Любой член арифметической прогрессии можно вычислить по формуле , где- член прогрессии с номеромn,- первый член иd – разность прогрессии.

Возьмём произвольное натуральное n. Из определения арифметической прогрессии следует

.

Эта цепочка состоит из nравенств, поэтому для любого конечногоn она может быть выписана. Следовательно, любой член арифметической прогрессии можно вычислить, зная его номер, первый член прогрессии и её разность.

Характеристическое свойство арифметической прогрессии.

Если последовательность является арифметической прогрессией, то все её члены, начиная со второго, являются средним арифметическим предшествующего и последующего членов.

Доказательство.

Из определения арифметической прогрессии получаем, что

.

Выразив из этого равенства , получим.

Теорема. (формула суммы n первых членов арифметической прогрессии).

Сумма n первых членов арифметической прогрессии равна .

Доказательство.

Запишем сумму n первых членов арифметической прогрессии двумя способами:

,

.

Сложим почленно эти два неравенства:

.

В каждой скобке стоит сумма , гдеk = 0,…, n – 1.

Преобразуем её, используя формулу n-го члена арифметической прогрессии,

Таких скобок ровно n, следовательно,. Теорема доказана.

Следствие.

Для доказательства нужно выразить по формулеn-го члена арифметической прогрессии и подставить в формулу для.